备考2024年中考数学核心素养专题二十二 圆的综合问题
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 在等腰直角三角形中, , D是边上一动点,连接 , 以为直径的圆交于点E , 则长的最小值是( )
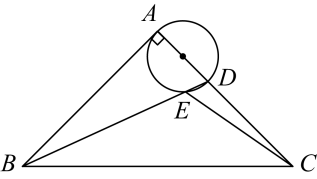 A、2 B、 C、 D、32. 如图,点P是外的一点,PA、PC是的切线,切点分别为A,C,AB是的直径,连接BC,PO,PO交弦AC于点D.下列结论中错误的是( )
A、2 B、 C、 D、32. 如图,点P是外的一点,PA、PC是的切线,切点分别为A,C,AB是的直径,连接BC,PO,PO交弦AC于点D.下列结论中错误的是( ) A、 B、 C、若 , 则△PAC是等边三角形 D、若△PAC是等边三角形,则3. 如图,AB是半圆O的直径,按以下步骤作图:
A、 B、 C、若 , 则△PAC是等边三角形 D、若△PAC是等边三角形,则3. 如图,AB是半圆O的直径,按以下步骤作图:
(1)分别以A,B为圆心,大于AO长为半径作弧,两弧交于点P,连接OP与半圆交于点C;(2)分别以A,C为圆心,大于AC长为半径作弧,两弧交于点Q,连接OQ与半圆交于点D;(3)连接AD,BD,BC,BD与OC交于点 E.根据以上作图过程及所作图形,下列结论:①BD平分∠ABC;②BC∥OD;③CE=OE;④AD2=OD•CE;所有正确结论的序号是( ) A、①② B、①④ C、②③ D、①②④4. 如图,在⊙O中,AB是⊙O的直径,AB=10, , 点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A、①② B、①④ C、②③ D、①②④4. 如图,在⊙O中,AB是⊙O的直径,AB=10, , 点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )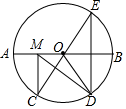 A、1 B、2 C、3 D、45. 如图,在中,弦BC,ED所对的圆心角分别是 , 与互补,已知.当时,弦BC与DE之间的距离等于( ).
A、1 B、2 C、3 D、45. 如图,在中,弦BC,ED所对的圆心角分别是 , 与互补,已知.当时,弦BC与DE之间的距离等于( ). A、7 B、1或7 C、 D、或6. 如图,的直径 , 是弦, , , , 的延长线与的延长线相交于点 , 的延长线与的延长线相交于点 , 连接 . 下列结论中正确的个数是( )
A、7 B、1或7 C、 D、或6. 如图,的直径 , 是弦, , , , 的延长线与的延长线相交于点 , 的延长线与的延长线相交于点 , 连接 . 下列结论中正确的个数是( )①;
②是的切线;
③B,E两点间的距离是;
④ .
 A、1 B、2 C、3 D、47. 如图,四边形中, , 以为直径的经过点C,连接、交于点.连接交于点 , 连接 , 若 , , 则以下结论:①;②为的切线;③;④;则正确的结论个数为( )
A、1 B、2 C、3 D、47. 如图,四边形中, , 以为直径的经过点C,连接、交于点.连接交于点 , 连接 , 若 , , 则以下结论:①;②为的切线;③;④;则正确的结论个数为( ) A、1 B、2 C、3 D、48. 如题图所示,已知一个半径为2的 , P为平面内一个点,过点P作的两条切线 , , 为的一条直径,且 , 连接若干条线段的端点.若 , 下列给出的四个命题中,为假命题的是( )
A、1 B、2 C、3 D、48. 如题图所示,已知一个半径为2的 , P为平面内一个点,过点P作的两条切线 , , 为的一条直径,且 , 连接若干条线段的端点.若 , 下列给出的四个命题中,为假命题的是( )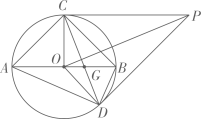 A、 B、为正三角形 C、 D、9. 如图,点A、B分别在x轴、y轴上();以为直径的圆经过原点O,C是的中点,连结 , . 下列结论:①;②;③若 , , 则的面积等于5;④若 , 则点C的坐标是 , 其中正确的结论有( )
A、 B、为正三角形 C、 D、9. 如图,点A、B分别在x轴、y轴上();以为直径的圆经过原点O,C是的中点,连结 , . 下列结论:①;②;③若 , , 则的面积等于5;④若 , 则点C的坐标是 , 其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个10. 如图,点E是的内心,连接AE并延长交BC于点F,交的外接圆于点D,连接BD.以下结论:①AE平分;②;③;④;⑤ , 其中正确的结论有( )
A、4个 B、3个 C、2个 D、1个10. 如图,点E是的内心,连接AE并延长交BC于点F,交的外接圆于点D,连接BD.以下结论:①AE平分;②;③;④;⑤ , 其中正确的结论有( )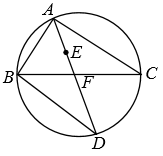 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 如图,圆内接四边形 , , 对角线平分 , 过点作交的延长线于点 , 若 , , 则的面积为 .
 12. 如图,在Rt△ABC中,∠C=90°,E为AB边上一点.以AE为直径的圆О与BC相切于点D,连结AD,BE= , BD=3.5.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为.
12. 如图,在Rt△ABC中,∠C=90°,E为AB边上一点.以AE为直径的圆О与BC相切于点D,连结AD,BE= , BD=3.5.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为. 13. 如图所示,为矩形中边上的一点,已知 , , 若点在矩形内部,且 , 则的最小值为 .
13. 如图所示,为矩形中边上的一点,已知 , , 若点在矩形内部,且 , 则的最小值为 .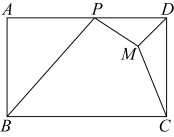 14. 中, , , , E是AC的中点,MN分别是边AB、BC上的动点,D也是BC边上的一个动点,以CD为直径作 , 连接ED交于F,连接FM,MN,则的最小值为.
14. 中, , , , E是AC的中点,MN分别是边AB、BC上的动点,D也是BC边上的一个动点,以CD为直径作 , 连接ED交于F,连接FM,MN,则的最小值为. 15. 如图, , , 分别是某圆内接正六边形、正方形、等边三角形的一边.若 , 下面四个结论中,
15. 如图, , , 分别是某圆内接正六边形、正方形、等边三角形的一边.若 , 下面四个结论中,①该圆的半径为2; ②的长为;
③平分; ④连接 , , 则与的面积比为 .
所有正确结论的序号是 .

三、解答题
-
16. 如图,在锐角中,是最短边.以为直径的 , 交于D , 过O作 , 交于E , 连接、、 .
 (1)、求证:;(2)、若 , , 求的度(3)、若 , , 求的长.17. 如图:四边形内接于圆 , , 对角线、交于 , 点在的延长线上,且 .
(1)、求证:;(2)、若 , , 求的度(3)、若 , , 求的长.17. 如图:四边形内接于圆 , , 对角线、交于 , 点在的延长线上,且 . (1)、判断与圆的位置关系,并说明理由;(2)、若 , 求证:为弧的中点;(3)、在(2)的条件下,若 , , 求劣弧的长度.18. 已知四边形内接于 , 直径于点F .
(1)、判断与圆的位置关系,并说明理由;(2)、若 , 求证:为弧的中点;(3)、在(2)的条件下,若 , , 求劣弧的长度.18. 已知四边形内接于 , 直径于点F . (1)、如图1,求证:;(2)、如图2,连接 , 若平分 , 过点D作于点H , 求证:;(3)、如图3,在(2)的条件下,连接交于点G , 若 , , 求的长.19. 如图,在Rt中, , 以AB为直径的与AC交于点 , 点是BC的中点,连结BD,DE
(1)、如图1,求证:;(2)、如图2,连接 , 若平分 , 过点D作于点H , 求证:;(3)、如图3,在(2)的条件下,连接交于点G , 若 , , 求的长.19. 如图,在Rt中, , 以AB为直径的与AC交于点 , 点是BC的中点,连结BD,DE (1)、求证:DE是的切线.(2)、若 , 求AD的长(3)、在(2)的条件下,点P是上一动点,求PA+PB的最大值.20. 如图1,⊙O的直径CD垂直弦AB于点E , 且CE=8,DE=2.
(1)、求证:DE是的切线.(2)、若 , 求AD的长(3)、在(2)的条件下,点P是上一动点,求PA+PB的最大值.20. 如图1,⊙O的直径CD垂直弦AB于点E , 且CE=8,DE=2. (1)、求AB的长.(2)、探究拓展:如图2,连接AC , 点G是上一动点,连接AG , 延长CG交AB的延长线于点F .
(1)、求AB的长.(2)、探究拓展:如图2,连接AC , 点G是上一动点,连接AG , 延长CG交AB的延长线于点F .①当点G是的中点时,求证:∠GAF=∠F;
②如图3,连接DF , BG , 当△CDF为等腰三角形时,请计算BG的长.
21. 如图,△ABD内接于半径为5的⊙O,连结AO并延长交BD于点M,交⊙O于点C,过点A作AE// BD,交CD的延长线于点E,AB=AM. (1)、求证:△ABM∽△ECA.(2)、当CM=4OM时,求AD的长.(3)、当CM= kOM时,设△MCD的面积为S1 , △ADE的面积为S2 ,求的值(用含k的代数式表示).22. 圆内接四边形若有一组邻边相等,则称之为等邻边圆内接四边形.
(1)、求证:△ABM∽△ECA.(2)、当CM=4OM时,求AD的长.(3)、当CM= kOM时,设△MCD的面积为S1 , △ADE的面积为S2 ,求的值(用含k的代数式表示).22. 圆内接四边形若有一组邻边相等,则称之为等邻边圆内接四边形. (1)、如图1,四边形为等邻边圆内接四边形, , , 直接写出的度数;(2)、如图2,四边形内接于 , 为的直径, , , 若四边形为等邻边圆内接四边形, , 求的长.(3)、如图3,四边形为等邻边圆内接四边形, , 为的直径,且.设 , 四边形的周长为 , 试确定与的函数关系式,并求出的最大值.23. 在平面直角坐标系中,已知圆和图形 , 将图形关于直线对称得到图形 , 为上任意一点,为圆上任意一点,将的最大值称为图形关于的“对称长度”.
(1)、如图1,四边形为等邻边圆内接四边形, , , 直接写出的度数;(2)、如图2,四边形内接于 , 为的直径, , , 若四边形为等邻边圆内接四边形, , 求的长.(3)、如图3,四边形为等邻边圆内接四边形, , 为的直径,且.设 , 四边形的周长为 , 试确定与的函数关系式,并求出的最大值.23. 在平面直角坐标系中,已知圆和图形 , 将图形关于直线对称得到图形 , 为上任意一点,为圆上任意一点,将的最大值称为图形关于的“对称长度”. (1)、若圆半径为;
(1)、若圆半径为;①在 , , 这三个点中,关于直线的“对称长度”为;
②已知直线: , 点 , , , , , , 则在线段 , , 中,关于的“对称长度”为的是;
(2)、圆半径为 , 已知点 , , , , , , 点在点的左侧,直线从开始,绕点顺时针旋转到 , 在旋转过程中,求正方形关于的“对称长度”的取值范围.24. 如图1,内接于圆为直径,点在的上方,且 . 连结是边上的高,过点作交的延长线于点 , 交于点 . (1)、求证: .(2)、当时,求的值.(3)、如图2,取的中点 , 连结 .
(1)、求证: .(2)、当时,求的值.(3)、如图2,取的中点 , 连结 .①若 , 在点运动的过程中,当四边形的其中一边长是的2倍时,求所有满足条件的的长.
②连结 , 当的面积是的面积的2倍时,则 ▲ (请直接写出答案)
四、综合题
-
25. 如图⊙O半径为r,锐角△ABC内接于⊙O,连AO并延长交BC于D,过点D作DE⊥AC于E.
 (1)、如图1,求证:∠DAB=∠CDE;(2)、如图1,若CD=OA,AB=6,求DE的长;(3)、如图2,当∠DAC=2∠DAB时,BD=5,DC=6,求r的值;(4)、如图3,若AE=AB=BD=1,直接写出AD+DE的值(用含r的代数式表示)26. 如图1,内接于 , 为直径,点D为上一点,连接交于点G,于点F交于点E.
(1)、如图1,求证:∠DAB=∠CDE;(2)、如图1,若CD=OA,AB=6,求DE的长;(3)、如图2,当∠DAC=2∠DAB时,BD=5,DC=6,求r的值;(4)、如图3,若AE=AB=BD=1,直接写出AD+DE的值(用含r的代数式表示)26. 如图1,内接于 , 为直径,点D为上一点,连接交于点G,于点F交于点E. (1)、求证:;(2)、如图2,连接 , 若 , 求证:;(3)、在(2)的条件下,如图3,点H是上一点,连接 , , 若 , 求线段的长.27. 在中,是的直径,弦与直径交于点 ,(1)、如图,求证: .
(1)、求证:;(2)、如图2,连接 , 若 , 求证:;(3)、在(2)的条件下,如图3,点H是上一点,连接 , , 若 , 求线段的长.27. 在中,是的直径,弦与直径交于点 ,(1)、如图,求证: .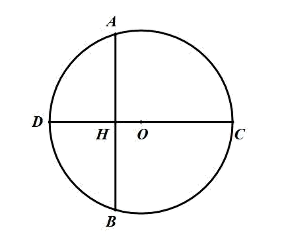 (2)、如图,点在延长线上,切于点交延长线于 , 连接交于 , 求证: .
(2)、如图,点在延长线上,切于点交延长线于 , 连接交于 , 求证: .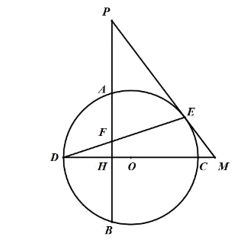 (3)、如图,在的条件下,连接和 , 连接交于点 , 若 , , 求的长.
(3)、如图,在的条件下,连接和 , 连接交于点 , 若 , , 求的长.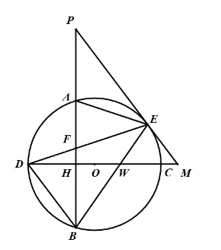 28. 已知在以点为原点、所在直线为轴的平面直角坐标系中,圆内接四边形的对角线、相交于 , 经过的内心,且抛物线经过、、三点.
28. 已知在以点为原点、所在直线为轴的平面直角坐标系中,圆内接四边形的对角线、相交于 , 经过的内心,且抛物线经过、、三点. (1)、求证:;(2)、求证:;(3)、、、四边形的面积分别记为 , 、S , 求同时满足以下三个条件的抛物线的解析式;
(1)、求证:;(2)、求证:;(3)、、、四边形的面积分别记为 , 、S , 求同时满足以下三个条件的抛物线的解析式;① ,
② ,
③四边形的周长为.
五、实践探究题
-
29.
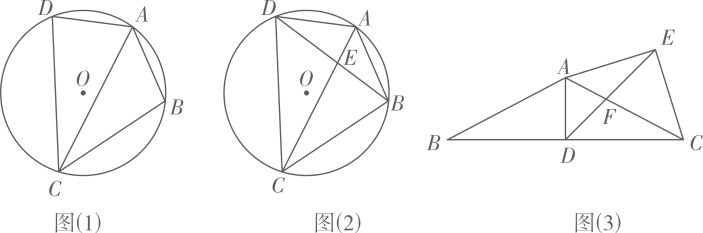 (1)、【感知】如图(1)已知四边形是圆O的内接四边形, , 易知 . (不用证明)(2)、【拓展】在【感知】的条件下,与交于点E,已知 , , 求的长.(3)、【应用】已知中 , 点D为中点,以为斜边向上作等腰直角三角形,当把的面积分为两部分时, .30. 如图1,扇形AOB中,∠AOB=90°,OA=6,点P在半径OB上,连接AP .
(1)、【感知】如图(1)已知四边形是圆O的内接四边形, , 易知 . (不用证明)(2)、【拓展】在【感知】的条件下,与交于点E,已知 , , 求的长.(3)、【应用】已知中 , 点D为中点,以为斜边向上作等腰直角三角形,当把的面积分为两部分时, .30. 如图1,扇形AOB中,∠AOB=90°,OA=6,点P在半径OB上,连接AP . (1)、把△AOP沿AP翻折,点O的对称点为点Q .
(1)、把△AOP沿AP翻折,点O的对称点为点Q .①当点Q刚好落在弧AB上,求弧AQ的长;
②如图2,点Q落在扇形AOB外,AQ与弧AB交于点C , 过点Q作QH⊥OA , 垂足为H ,
探究OH、AH、QC之间的数量关系,并说明理由;
(2)、如图3,记扇形AOB在直线AP上方的部分为图形W , 把图形W沿着AP翻折,点B的对称点为点E , 弧AE与OA交于点F , 若OF=2,求PO的长.