备考2024年中考数学核心素养专题二十一 几何图形的存在性问题
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:
①存在无数个平行四边形 ;
②存在无数个矩形 ;
③存在无数个菱形 ;
④存在无数个正方形 .其中正确的个数是( )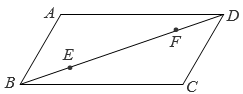 A、1 B、2 C、3 D、42. 如图,一副三角板( , , ), , 顶点A重合,将绕其顶点A旋转,在旋转过程中(不添加辅助线),以下4种位置不存在相似三角形的是( )A、
A、1 B、2 C、3 D、42. 如图,一副三角板( , , ), , 顶点A重合,将绕其顶点A旋转,在旋转过程中(不添加辅助线),以下4种位置不存在相似三角形的是( )A、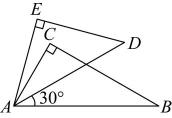 B、
B、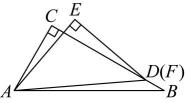 C、
C、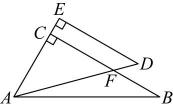 D、
D、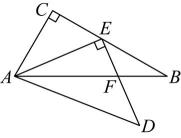 3. 如图,直线 , 直线分别交 , 于点 , , 以点B为圆心,长为半径画弧,若在弧上存在点C使 , 则的度数是( )
3. 如图,直线 , 直线分别交 , 于点 , , 以点B为圆心,长为半径画弧,若在弧上存在点C使 , 则的度数是( )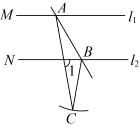 A、 B、 C、 D、4. 题目:“如图,在矩形中, , , P,Q分别是上的点.”张老师要求添加条件后,编制一道题目,并解决,甲、乙两人的做法如下.下列判断正确的是( )
A、 B、 C、 D、4. 题目:“如图,在矩形中, , , P,Q分别是上的点.”张老师要求添加条件后,编制一道题目,并解决,甲、乙两人的做法如下.下列判断正确的是( )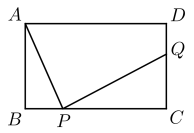
甲:若 , 则在BC上存在2个点P,使与相似;
乙:若 , 则的最大值为
A、甲对乙错 B、甲错乙对 C、甲、乙都对 D、甲、乙都错5. 如图所示,矩形ABCD中,AD=a,AB=b,若要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系一定满足( ).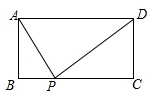 A、 B、 C、 D、6. 如图,在中, , 点D、E分别是的中点.将绕点A顺时针旋转 , 射线与射线交于点P,在这个旋转过程中有下列结论:
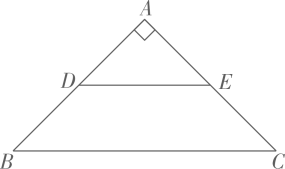
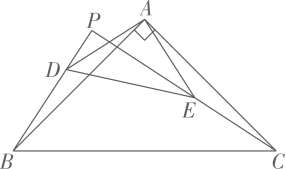
A、 B、 C、 D、6. 如图,在中, , 点D、E分别是的中点.将绕点A顺时针旋转 , 射线与射线交于点P,在这个旋转过程中有下列结论:①;②存在最大值为;③存在最小值为;④点P运动的路径长为 . 其中,正确的是( )
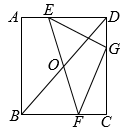
 A、①③④ B、①②④ C、①②③ D、②③④7. 如图,矩形中, , E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点, , 连接 , . 甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.
A、①③④ B、①②④ C、①②③ D、②③④7. 如图,矩形中, , E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点, , 连接 , . 甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.甲:存在点E,使;
乙:的面积存在最小值.
下列说法正确的是( )
 A、甲、乙都正确 B、甲、乙都错误 C、甲正确,乙错误 D、甲错误,乙正确8. 两块完全相同的含角的直角三角板和重合在一起,将三角板绕直角顶点按逆时针方向旋转 , 如图所示.以下结论错误的是( )
A、甲、乙都正确 B、甲、乙都错误 C、甲正确,乙错误 D、甲错误,乙正确8. 两块完全相同的含角的直角三角板和重合在一起,将三角板绕直角顶点按逆时针方向旋转 , 如图所示.以下结论错误的是( )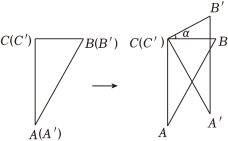 A、当时,与的交点恰好为中点.
A、当时,与的交点恰好为中点.
B、当时,恰好经过点 .
C、在旋转过程中,存在某一时刻,使得 .
D、在旋转过程中,始终存在 .9. 某兴趣小组开展综合实践活动:在中, , 为上一点,动点以每秒1个单位的速度从点出发,在三角形边上沿匀速运动,到达点时停止,以为边作正方形 , 设点的运动时间为 , 正方形的面积为 , 当点由点运动到点时,经探究发现是关于的二次函数,并绘制成如图2所示的图象,若存在3个时刻对应的正方形DPEF的面积均相等,当时,则正方形的面积为( )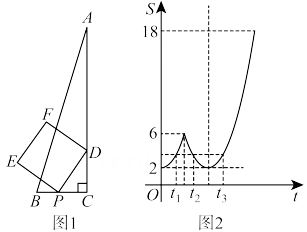 A、3 B、 C、4 D、510. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )
A、3 B、 C、4 D、510. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )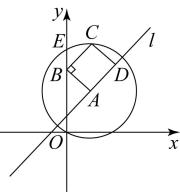 A、12 B、 C、 D、
A、12 B、 C、 D、二、填空题
-
11. 如图,在平行四边形ABCD中,AD=2AB=2, ∠ABC=60°,E,F是对角线BD上的动点,且BE= DF,M,N分别是边AD,BC上的动点.有下列四种说法:
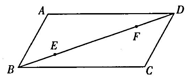
①存在无数个平行四边形 MENF;
②存在无数个矩形MENF;
③存在无数个菱形MENF;
④存在无数个正方形MENF.其中正确的是(填序号).
12. 已知的半径为 , 的半径为 , 圆心距 , 如果在上存在一点 , 使得 , 则的取值范围是 .13. 如题图所示,在中存在一面积为的内切圆,其圆心为点 , 连接 , 若满足 , , , 则实数的值为 .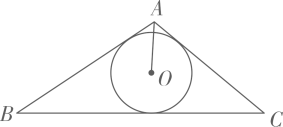 14. 如图,在边长为的正方形中,点在边上,且点是边上的动点,连接 , 将线段绕点顺时针旋转得到线段若在正方形内还存在一点 , 则点到点、点、点的距离之和的最小值为 .
14. 如图,在边长为的正方形中,点在边上,且点是边上的动点,连接 , 将线段绕点顺时针旋转得到线段若在正方形内还存在一点 , 则点到点、点、点的距离之和的最小值为 .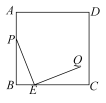 15. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P , 使得△CMP为“智慧三角形”,则点P的坐标为: .
15. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P , 使得△CMP为“智慧三角形”,则点P的坐标为: .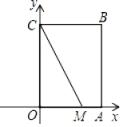 16. 如图,在Rt△ABC中,∠C=90°,记x=AC,y=BC-AC,在平面直角坐标系xOy中,定义(x,y)为这个直角三角形的坐标,Rt△ABC为点(x,y)对应的直角三角形.有下列结论:①在x轴正半轴上的任意点(x,y)对应的直角三角形均满足AB=BC;②在函数y=(x>0)的图象上存在两点P,Q,使得它们对应的直角三角形相似;③对于函数y=(x-2020)2-1(x>0)的图象上的任意一点P,都存在该函数图象上的另一点Q,使得这两个点对应的直角三角形相似;④在函数y=-2x+2020(x>0)的图象上存在无数对点P,Q(P与Q不重合),使得它们对应的直角三角形全等.所有正确结论的序号是 .
16. 如图,在Rt△ABC中,∠C=90°,记x=AC,y=BC-AC,在平面直角坐标系xOy中,定义(x,y)为这个直角三角形的坐标,Rt△ABC为点(x,y)对应的直角三角形.有下列结论:①在x轴正半轴上的任意点(x,y)对应的直角三角形均满足AB=BC;②在函数y=(x>0)的图象上存在两点P,Q,使得它们对应的直角三角形相似;③对于函数y=(x-2020)2-1(x>0)的图象上的任意一点P,都存在该函数图象上的另一点Q,使得这两个点对应的直角三角形相似;④在函数y=-2x+2020(x>0)的图象上存在无数对点P,Q(P与Q不重合),使得它们对应的直角三角形全等.所有正确结论的序号是 .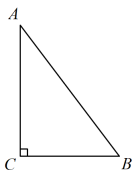 17. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=6,BD=2,以点B为圆心,BD长为半径作圆,点E为上的动点,连结EC,作FC⊥CE,垂足为C,点F在直线BC的上方,且满足 , 连结BF.当点E与点D重合时,BF的值为.点E在上运动过程中,BF存在最大值为.
17. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=6,BD=2,以点B为圆心,BD长为半径作圆,点E为上的动点,连结EC,作FC⊥CE,垂足为C,点F在直线BC的上方,且满足 , 连结BF.当点E与点D重合时,BF的值为.点E在上运动过程中,BF存在最大值为.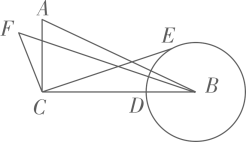
三、解答题
-
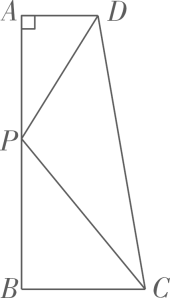
18. 如图所示,已知在四边形ABCD中, , .在线段AB上是否存在一点 , 使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似?若存在,这样的点有几个?若不存在.请说明理由.
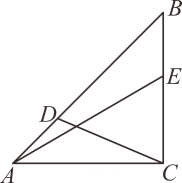
 19. 已知二次函数y=ax2+bx+c的图象过点 , 且对任意实数x,都有.二次函数与x轴的正半轴交点为A,与y轴交点为C;点M是中二次函数图象上的动点.在x轴上存在点N,使得以A、C、M、N为顶点的四边形是平行四边形.请求出所有满足条件的点N的坐标.20. 平面上有n个点(n≥3,n为自然数),其中任何三点不在同一直线上.证明:一定存在三点,以这三点作为顶点的三角形中至少有一个内角不大于 .21. 数学课上,老师给出题目:如图所示,在中 , , 点D , E分别是边和边上的动点,且 , 连接 , . 请探究是否存在最小值?并说明理由.
19. 已知二次函数y=ax2+bx+c的图象过点 , 且对任意实数x,都有.二次函数与x轴的正半轴交点为A,与y轴交点为C;点M是中二次函数图象上的动点.在x轴上存在点N,使得以A、C、M、N为顶点的四边形是平行四边形.请求出所有满足条件的点N的坐标.20. 平面上有n个点(n≥3,n为自然数),其中任何三点不在同一直线上.证明:一定存在三点,以这三点作为顶点的三角形中至少有一个内角不大于 .21. 数学课上,老师给出题目:如图所示,在中 , , 点D , E分别是边和边上的动点,且 , 连接 , . 请探究是否存在最小值?并说明理由.嘉淇的想法是把和转移到某处,并使它们“接在一起”,然后利用“两点之间,线段最短”尝试探索,并成功解决了问题.以下是她的探索思路,请你按要求补充具体解题过程.
 (1)、在射线上取点F , 使 , 把绕点A顺时针旋转,使点D落在点F处,点C落在点G处.
(1)、在射线上取点F , 使 , 把绕点A顺时针旋转,使点D落在点F处,点C落在点G处.①请你运用尺规作图(保留作图痕迹,不用给出证明),作出 , 并连接;
②求证: .
(2)、在(1)的基础上,请你通过探索,求出的最小值,并直接写出此时的长度.22. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .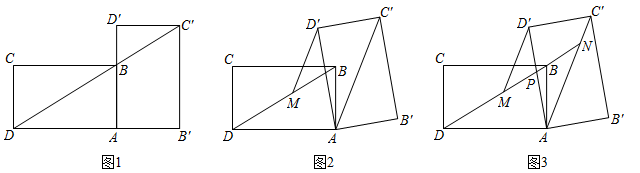
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
四、综合题
-
23. 对于平面直角坐标系中的线段 , 给出如下定义:若存在使得 , 则称为线段的“等幂三角形”,点R称为线段的“等幂点”.
 (1)、已知 , 若存在等腰是线段的“等幂三角形”,求点B的坐标;(2)、已知点C的坐标为 , 点D在直线上,记图形M为以点为圆心,2为半径的位于x轴上方的部分.若图形M上存在点E,使得线段的“等幂三角形”为锐角三角形,直接写出点D的横坐标的取值范围.24. 在平面直角坐标系中,对于和点不与点重合给出如下定义:若边 , 上分别存在点 , 点 , 使得点与点关于直线对称,则称点为的“翻折点”.(1)、已知 ,
(1)、已知 , 若存在等腰是线段的“等幂三角形”,求点B的坐标;(2)、已知点C的坐标为 , 点D在直线上,记图形M为以点为圆心,2为半径的位于x轴上方的部分.若图形M上存在点E,使得线段的“等幂三角形”为锐角三角形,直接写出点D的横坐标的取值范围.24. 在平面直角坐标系中,对于和点不与点重合给出如下定义:若边 , 上分别存在点 , 点 , 使得点与点关于直线对称,则称点为的“翻折点”.(1)、已知 ,
若点与点重合,点与点重合,直接写出的“翻折点”的坐标;
是线段上一动点,当是的“翻折点”时,求长的取值范围;(2)、直线与轴,轴分别交于 , 两点,若存在以直线为对称轴,且斜边长为的等腰直角三角形,使得该三角形边上任意一点都为的“翻折点”,直接写出的取值范围.25. 问题背景:如图1,在等腰中, , , 垂足为点D,在中, , , 连接中点,连接 , 在绕点A旋转过程中,线段之间存在怎样的数量关系?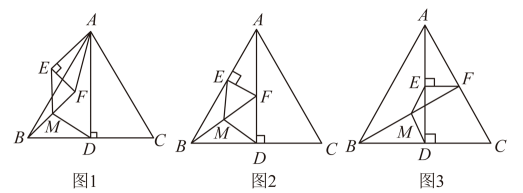 (1)、 观察发现:
(1)、 观察发现:为了探究线段和之间的数量关系,可先将图形位置特殊化,将绕点A旋转,使重合,如图2,易知和之间的数量关系为;
(2)、 操作证明:继续将绕点A旋转,使与重合时,如图3,(1)中线段之间的数量关系仍然成立,请加以证明.
(3)、 问题解决:根据上述探究的经验,我们回到一般情况,如图1,在其他条件不变的情况下,上述的结论还成立吗?请说明你的理由.
26. 在平面直角坐标系xOy中,对于第一象限的P , Q两点,给出如下定义:若y轴正半轴上存在点 , 轴正半轴上存在点 ,使 ,且 (如图1),则称点P与点Q为 -关联点.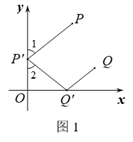 (1)、在点 , 中,与 为45°-关联点的是;(2)、如图2, , , .若线段 上存在点Q,使点P与点Q为45°-关联点,结合图象,求m的取值范围;
(1)、在点 , 中,与 为45°-关联点的是;(2)、如图2, , , .若线段 上存在点Q,使点P与点Q为45°-关联点,结合图象,求m的取值范围;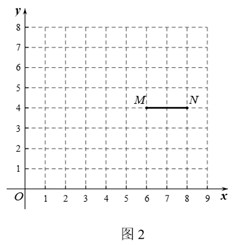 (3)、已知点 , .若线段 上至少存在一对30°-关联点,直接写出n的取值范围.27. 给定图形和点 , , 若图形上存在两个不重合的点 , , 使得点关于点的对称点与点关于点的对称点重合,则称点与点关于图形双对合.在平面直角坐标系中,已知点 , , .(1)、在点 , , 中,与点关于线段双对合的点是;(2)、点是轴上一动点,的直径为1.
(3)、已知点 , .若线段 上至少存在一对30°-关联点,直接写出n的取值范围.27. 给定图形和点 , , 若图形上存在两个不重合的点 , , 使得点关于点的对称点与点关于点的对称点重合,则称点与点关于图形双对合.在平面直角坐标系中,已知点 , , .(1)、在点 , , 中,与点关于线段双对合的点是;(2)、点是轴上一动点,的直径为1.①若点与点关于双对合,求的取值范围;
②当点运动时,若上存在一点与上任意一点关于双对合,直接写出点的横坐标的取值范围.
28. 对于平面直角坐标系 中的线段 ,给出如下定义:若存在 使得 ,则称 为线段 的“等幂三角形”,点R称为线段 的“等幂点”. (1)、已知 .
(1)、已知 .①在点 中,线段 的“等幂点”是 ▲ ;
②若存在等腰 是线段 的“等幂三角形”,求点B的坐标;
(2)、已知点C的坐标为 ,点D在直线 上,记图形M为以点 为圆心,2为半径的 位于x轴上方的部分.若图形M上存在点E , 使得线段 的“等幂三角形” 为锐角三角形,直接写出点D的横坐标 的取值范围.29. 定义:在一个三角形中,若存在两条边x和y , 使得数量上y=x2 , 则称此三角形为“平方三角形”,x称为平方边.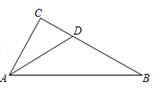 (1)、如图,△ABC中 , ∠C=90°,∠B=∠CAD , D是BC边上一点.CD=1,证明△ABC是平方三角形;(2)、在(1)的条件下,若AC=2,求tan∠DAB .(3)、若a , b , c是平方三角形的三条边,平方边a=2,若三角形中存在一个角为60°,求c的值;
(1)、如图,△ABC中 , ∠C=90°,∠B=∠CAD , D是BC边上一点.CD=1,证明△ABC是平方三角形;(2)、在(1)的条件下,若AC=2,求tan∠DAB .(3)、若a , b , c是平方三角形的三条边,平方边a=2,若三角形中存在一个角为60°,求c的值;五、实践探究题
-
30. 已知P为△ABC所在平面内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,若存在一个三角形与△ABC相似(全等除外)那么就称P为△ABC的共相似点”根据“共相似点“是否落在三角形的内部,边上或外部,可将其分为内共相似点”,“边共相似点或“外共相似点”.
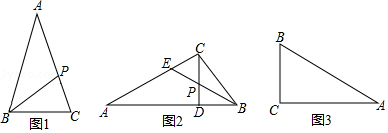 (1)、据定义可知,等边三角形(填“存在”或“不存在)共相似点(2)、如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.
(1)、据定义可知,等边三角形(填“存在”或“不存在)共相似点(2)、如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.【探究】用边共相似点探究三角形的形状
【探究2】用内共相似点探究三角形的内角关系
(3)、如图2,在△ABC中,∠A<∠B<∠C,高线CD与角平分线BE交于点P,若P是△ABC的一个内共相似点试说明点E是△ABC的边共相似点,并直接写出∠A的度数;【探究】探究直角三角形共相似点的个数
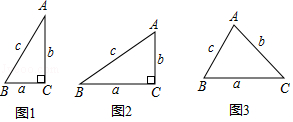
(4)、如图3,在R△ABC中,∠C=90°,∠A=30°,BC= ,若△PBC与△ABC相以,则满足条件的P点共有个.31. 阅读材料,回答问题:小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= ,AB=c=2,那么 = =2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着 = = 的关系.
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
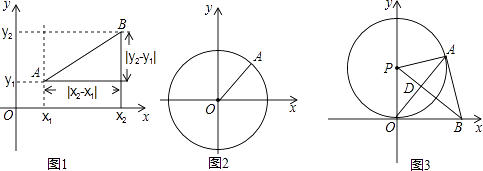
(1)、如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“ = = ”的关系是否成立?(2)、完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“ = = ”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).32. 阅读资料:如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1 , y1),B(x2 , y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A,B两点间的距离为AB= .
我们知道,圆可以看成到圆心的距离等于半径的点的集合,如图2,在平面直角坐标系xOy中,A (x,y)为圆上任意一点,则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 , 当⊙O的半径OA为r时,⊙O的方程可写为:x2+y2=r2 .
问题拓展:
如果圆心坐标为P (a,b),半径为r,那么⊙P的方程可以写为 (x﹣a)2+(y﹣b)2=r2 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以点Q为圆心,OQ长为半径的⊙Q的方程;若不存在,说明理由.