备考2024年中考数学核心素养专题二十数与式的存在性问题

试卷更新日期：2024-03-31 类型：二轮复习

进入出卷网下载

一、选择题

1. 若关于 $x$ 的不等式 $2 x - a > 0$ 的解集中存在负数解，但不存在负整数解，则 $a$ 的取值范围是（）.

A、 $a \geq - 2$ B、 $a < 0$ C、 $- 2 \leq a < 0$ D、 $- 2 < a \leq 0$

查看试题解析
2. 若a和b都是正整数且 $a < b ， \sqrt{a}$ 和 $\sqrt{b}$ 是可以合并的二次根式
结论I：存在两组a和b的值使得 $\sqrt{a} + \sqrt{b} = \sqrt{75}$ ；
结论Ⅱ：不存在a和b的值使得 $\sqrt{a} + \sqrt{b} = \sqrt{260}$ ．
针对结论I和Ⅱ，下列判断正确的是（）

A、I和Ⅱ都对 B、I和Ⅱ都不对 C、I不对II对 D、I对Ⅱ不对

查看试题解析
3. 设 $x$ 为正整数，则存在正整数 $a$ 和 $b$ ，使得 $\frac{1 + b - 2 a}{a^{2} - b} = x$ ，则 $a$ 、 $b$ 的值分别为（）.

A、 $x + 2$ ， $x^{2} + 3 x + 3$ B、 $x + 2$ ， $x^{2} + 2 x + 2$ C、 $x - 2$ ， $x^{2} - 3 x + 3$ D、 $x + 1$ ， $x^{2} + x + 1$

查看试题解析
4. 在平面直角坐标系 $x O y$ 中，对于横、纵坐标相等的点称为“完美点”.下列函数的图象中不存在“完美点”的是（）

A、 $y = - x$ B、 $y = \frac{3}{x}$ C、 $y = x + 3$ D、 $y = x^{2} - 3 x$

查看试题解析
5. 对多项式 $x - y - z - m - n$ 任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如： $(x - y) - (z - m - n) = x - y - z + m + n$ ， $x - y - (z - m) - n = x - y - z + m - n$ ， …，给出下列说法：
①至少存在一种“加算操作”，使其结果与原多项式相等；
②不存在任何“加算操作”，使其结果与原多项式之和为0；
③所有的“加算操作”共有8种不同的结果.
以上说法中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
6. 对于五个整式， $A$ ： $2 x^{2}$ ； $B$ ： $x + 1$ ； $C$ ： $- 2 x$ ； $D$ ： $y^{2}$ ； $E$ ： $2 x - y$ 有以下几个结论：
$①$ 若 $y$ 为正整数，则多项式 $B \cdot C + A + D + E$ 的值一定是正数；
$②$ 存在实数 $x$ ， $y$ ，使得 $A + D + 2 E$ 的值为 $- 2$ ；
$③$ 若关于 $x$ 的多项式 $M = 3 (A - B) + m \cdot B \cdot C (m$ 为常数 $)$ 不含 $x$ 的一次项，则该多项式 $M$ 的值一定大于 $- 3$
上述结论中，正确的个数是（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
7. 已知 $y_{1}$ 和 $y_{2}$ 均是以 $x$ 为自变量的函数，当 $x = m$ 时，函数值分别是 $M_{1}^{}$ 和 $M_{2}$ ，若存在实数 $m$ ，使得 $M_{1}^{} + M_{2} = 0$ ，则称函数 $y_{1}$ 和 $y_{2}$ 具有性质P。以下函数 $y_{1}$ 和 $y_{2}$ 具有性质P的是（）

A、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x - 1$ B、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x + 1$ C、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x - 1$ D、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x + 1$

查看试题解析
8. 二次函数 $y = x^{2}$ 的图象上有两个不同的点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，给出下列推断：
① 对任意的 $x_{1} < x_{2}$ ，都有 $y_{1} < y_{2}$ ；② 对任意的 $x_{1} + x_{2} = 0$ ，都有 $y_{1} = y_{2}$ ；③ 存在 $x_{1}$ ， $x_{2}$ ，满足 $x_{1} + x_{2} = 0$ ，且 $y_{1} + y_{2} = 0$ ；④ 对于任意的正实数 $t$ ，存在 $x_{1}$ ， $x_{2}$ ，满足 $| x_{1} - x_{2} | = 1$ ，且 $| y_{1} - y_{2} | = t$ .
以上推断中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 在多项式x-y-z-m-n（其中x＞y＞z＞m＞n）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如：x-y-|z-m|-n＝x-y-z+m-n ， |x-y|-z-|m-n|＝x-y-z-m+n ， …．下列说法：
①存在“绝对操作”，使其运算结果与原多项式相等；
②不存在“绝对操作”，使其运算结果与原多项式之和为0；
③所有的“绝对操作”共有7种不同运算结果．
其中正确的个数是（　　）

A、0 B、1 C、2 D、3

查看试题解析
10. 已知 $y_{1}$ 和 $y_{2}$ 均是以 $x$ 为自变量的函数， $a$ 为实数.当 $x = m$ 时，函数值分别为 $M_{1}$ 和 $M_{2}$ ，若存在实数 $m$ ，使得 $M_{1} = M_{2}$ .则称 $y_{1}$ 和 $y_{2}$ 为友好函数，以下 $y_{1}$ 和 $y_{2}$ 不一定是友好函数的是（）

A、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = 3 x + 1$ B、 $y_{1} = x^{2} + a - \frac{1}{2}$ 和 $y_{2} = - a x + \frac{a}{4}$ C、 $y_{1} = - \frac{2}{x}$ 和 $y_{2} = x - 3$ D、 $y_{1} = \frac{a + 2}{x}$ 和 $y_{2} = x + a$

查看试题解析
11. 若一个点的纵坐标是横坐标的3倍，则称这个点为“三倍点”，如： $A (1 ， 3) ， B (- 2 ， - 6) ， C (0 ， 0)$ 等都是三倍点”，在 $- 3 < x < 1$ 的范围内，若二次函数 $y = - x^{2} - x + c$ 的图象上至少存在一个“三倍点”，则c的取值范围是（）

A、 $- \frac{1}{4} \leq c < 1$ B、 $- 4 \leq c < - 3$ C、 $- \frac{1}{4} < c < 5$ D、 $- 4 \leq c < 5$

查看试题解析

二、填空题

12. 已知y是关于x的函数，若该函数的图象经过点 $P (t ， t)$ ，则称点P为函数图象上的“平衡点”，例如：直线 $y = - 2 x + 3$ 上存在“平衡点” $P (1 ， 1)$ ，若函数 $y = (m - 1) x^{2} - 3 x + 2 m$ 的图象上存在唯一“平衡点”，则m= ．

查看试题解析
13. 若 $x$ ， $y$ 满足 $x^{2} = 4 y + t$ ， $y^{2} = 4 x + t$ 且 $x \neq y (t$ 为常数），则称点 $M (x ， y)$ 为“和谐点”．一次函数 $y = 2 x + b (- 3 \leq x \leq 1)$ 存在“和谐点”，则b的取值范围．

查看试题解析
14. 已知关于x的不等式组 ${\begin{array}{l} x - a < 0 ， \\ 2 x - 1 \geq 7 \end{array}$ 至少有两个整数解，且存在以3，a，7为边的三角形，则a的整数解有个．

查看试题解析
15. 抛物线 $y = 2 x^{2} - a x + m - a$ 与 $x$ 轴相交于不同两点 $A (x_{1} ， 0)$ 、 $B (x_{2} ， 0)$ ，若存在整数 $a$ 及整数 $m$ ，使得 $1 < x_{1} < 3$ 和 $1 < x_{2} < 3$ 同时成立，则 $m =$ ．

查看试题解析
16. 定义：在平面直角坐标系中，对于点 $P (x_{1} ， y_{1})$ ，当点 $Q (x_{2} ， y_{2})$ 满足 $2 (x_{1} + x_{2}) = y_{1} + y_{2}$ 时，称点 $Q (x_{2} ， y_{2})$ 是点 $P (x_{1} ， y_{1})$ 的“倍增点”．已知点 $P_{1} (1 ， 0)$ ，则正确的结论有．（填写序号）
①点 $Q_{1} (3 ， 8) ， Q_{2} (- 2 ， - 2)$ 都是点 $P_{1}$ 的“倍增点”；
②若直线 $y = x + 2$ 上的点A是点 $P_{1}$ 的“倍增点”，则点A的坐标为 $(2 ， 4)$ ；
③抛物线 $y = x^{2} - 2 x - 3$ 上存在两个点是点 $P_{1}$ 的“倍增点”；

查看试题解析
17. 新定义：若一个点的纵坐标是横坐标的2倍，则称这个点为二倍点．若二次函数y＝x²﹣x+c（c为常数）在﹣2＜x＜4的图象上存在两个二倍点，则c的取值范围是．

查看试题解析

三、解答题

18. 已知 $x_{1}$ ， $x_{2}$ 是关于x的方程 $x^{2} + 2 (m - 2) x + m^{2} + 4 = 0$ 的两个根，是否存在实数m使 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} = 21$ 成立？若存在，求出m的值；若不存在，说明理由.

查看试题解析
19. 已知m，n是方程x²﹣2x﹣1＝0的两个根，是否存在实数a使﹣（m+n）（7m²﹣14m+a）（3n²﹣6n﹣7）的值等于8？若存在，求出a的值；若不存在，请说明理由.

查看试题解析
20. 已知：关于x的方程 $x^{2} + (8 - 4 m) x + 4 m^{2} = 0$ 是否存在实数m，使方程的两个实数根的平方和等于 $136$ ？若存在，请求出满足条件的m值；若不存在，请说明理由.

查看试题解析
21. 如图，抛物线y＝﹣x²+bx+c与x轴交于A（2，0），B（﹣4，0）两点．
（Ⅰ）求抛物线的解析式；

（Ⅱ）若抛物线交y轴于点C，在抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由；

（Ⅲ）在抛物线第二象限的图象上是否存在一点P，使得△PBC的面积最大？若存在，请直接写出点P的坐标和△PBC面积的最大值；若不存在，请说明理由．

查看试题解析
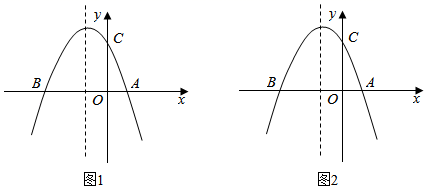22. 若定义：若一个函数图象上存在纵坐标是横坐标2倍的点，则把该函数称为“明德函数”，该点称为“明德点”，例如：“明德函数” $y = x + 1$ ，其“明德点”为 $(1 ， 2)$ .

(1)、①判断：函数 $y = 2 x + 3$ “明德函数”（填“是”或“不是”）；
②函数 $y = x^{2}$ 的图像上的明德点是；

(2)、若抛物线 $y = (m - 1) x^{2} + m x + \frac{1}{4} m$ 上有两个“明德点”，求 $m$ 的取值范围；

(3)、若函数 $y = x^{2} + (m - k + 2) x + \frac{n}{4} - \frac{1}{2} k$ 的图象上存在唯一的一个“明德点”，且当 $- 1 \leq m \leq 3$ 时， $n$ 的最小值为 $k$ ，求 $k$ 的值.

查看试题解析

四、综合题

23. （概念认识）
已知m是实数，若某个函数图象上存在点M（m，m），则称点M是该函数图象上的“固定点”.

（数学理解）

(1)、一次函数y＝－2x＋3的图象上的“固定点”的坐标是；

(2)、求证：反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象上存在2个“固定点”；

(3)、将二次函数y＝x²＋bx＋1（b＜－2）的图象在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分保持不变，翻折后的图象与原图象在x轴上方的部分组成一个类似“W”形状的新图象.若新图象上恰好存在3个“固定点”，求b的值.

查看试题解析
24. 新定义：已知y是x的函数，若函数图象上存在一点P（a，a+2），则称点P为函数图象上的“朴实点”．例如：直线y＝2x+1上存在的“朴实点”是P（1，3）．

(1)、判断直线y＝ $\frac{1}{3}$ x+4上是否有“朴实点”？若有，直接写出其坐标；若没有，请说明理由；

(2)、若抛物线y＝x²+3x+2-k上存在两个“朴实点”，两个“朴实点”之间的距离为2 $\sqrt{2}$ ，求k的值；

(3)、若二次函数y＝ $\frac{1}{8}$ x²+（m-t+1）x+2n+2t-2的图象上存在唯一的“朴实点”，且当-2≤m≤3时，n的最小值为t+4，求t的值．

查看试题解析
25. 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于直线x＝n（n为常数）对称，则把该函数称之为“X（n）函数”.

(1)、在下列关于x的函数中，是“X（n）函数”的，请在相应题目后面的括号中打“√”，不是“X（n）函数”的打“×”.
① $y = \frac{m}{x}$ （ $m \neq 0$ ）（   ）

② $y = | 2 x |$ （   ）

③ $y = x^{2} + 2 x - 5$ （   ）

(2)、若关于x的函数 $y = | x - h |$ （h为常数）是“X（2）函数”，与 $y = | \frac{m}{x} |$ （m为常数， $m > 0$ ）相交于A（xA，yA）、B（xB，yB）两点，A在B的左边， $x_{B} - x_{A} = 4$ ，求m的值；

(3)、若关于x的“X（n）函数” $y = a x^{2} + b x + 4$ （a，b为常数）经过点（ $- 1$ ，1），且n＝1，当 $t - 1 \leq x \leq t$ 时，函数的最大值为y₁ ，最小值为y² ，且 $y_{1} - y_{2} = 2$ ，求t的值.

查看试题解析
26. 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于y轴对称，则把该函数称之为“T函数”，其图象上关于y轴对称的不同两点叫做一对“T点”．根据该约定，完成下列各题．

(1)、若点A（1，r）与点B（s，4）是关于x的“T函数”y＝ ${\begin{array}{l} - \frac{4}{x} (x < 0) \\ t x^{2} (x \geq 0 ， t \neq 0 ， t) \end{array}$ 的图象上的一对“T点”，则r＝， s＝， t＝（将正确答案填在相应的横线上）；

(2)、关于x的函数y＝kx+p（k，p是常数）是“T函数”吗？如果是，指出它有多少对“T点”如果不是，请说明理由；

(3)、若关于x的“T函数”y＝ $a x^{2} + b x + c$ （a＞0，且a，b，c是常数）经过坐标原点O，且与直线l：y＝mx+n（m≠0，n＞0，且m，n是常数）交于M（ $x_{1}$ ， $y_{1}$ ），N（ $x_{2}$ ， $y_{2}$ ）两点，当 $x_{1}$ ， $x_{2}$ 满足 $(1 - x_{1})^{- 1} + x_{2} = 1$ 时，直线l是否总经过某一定点？若经过某一定点，求出该定点的坐标；否则，请说明理由．

查看试题解析
27. 规定：如果两个函数图象上至少存在一对点是关于原点对称的，我们则称这两个函数互为“守望函数”，这对点称为“守望点”．例如：点P（2，4）在函数 $y = x^{2}$ 上，点Q（ $- 2$ ， $- 4$ ）在函数 $y = - 2 x - 8$ 上，点P与点Q关于原点对称，此时函数 $y = x^{2}$ 和 $y = - 2 x - 8$ 互为“守望函数”，点P与点Q则为一对“守望点”．

(1)、函数 $y = - 2 x - 1$ 和函数 $y = 4 x$ 是否互为“守望函数”？若是，求出它们的“守望点”，若不是，请说明理由；

(2)、已知函数 $y = x^{2} + 2 x$ 和 $y = 4 x + n - 2022$ 互为“守望函数”，求n的最大值并写出取最大值时对应的“守望点”；

(3)、已知二次函数 $y = a x^{2} + b x + c$ $(a > 0)$ 与 $y = 2 b x + 1$ 互为“守望函数”，有且仅有一对“守望点”，若二次函数的顶点为M，与x轴交于 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ ，其中 $0 < x_{1} < x_{2}$ ， $A B = 2$ ，又 $a = \frac{4 c}{c^{2} - c + 6}$ ，过顶点M作x轴的平行线l交y轴于点N，直线 $y = 2 b x + 1$ 与y轴交点为点Q，动点E在x轴上运动，求抛物线 $y = a x^{2} + b x + c$ $(a > 0)$ 上的一点F的坐标，使得四边形 $F Q E N$ 为平行四边形．

查看试题解析
28. 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于y轴对称，则把该函数称之为“T函数”，其图象上关于y轴对称的不同两点叫做一对“T点”.根据该约定，完成下列各题.

(1)、若点A（1，r）与点B（s，4）是关于x的“T函数” $y = {\begin{array}{l} - \frac{4}{x} (x < 0) \\ t x^{2} (x \geq 0 ， t \neq 0 ， t 是常数) \end{array}$ 的图象上的一对“T点”，则r＝， s＝， t＝（将正确答案填在相应的横线上）；

(2)、关于x的函数y＝kx+p（k，p是常数）是“T函数”吗？如果是，指出它有多少对“T点”如果不是，请说明理由；

(3)、若关于x的“T函数”y＝ax²+bx+c（a＞0，且a，b，c是常数）经过坐标原点O，且与直线l：y＝mx+n（m≠0，n＞0，且m，n是常数）交于M（x₁ ， y₁），N（x₂ ， y₂）两点，当x₁ ， x₂满足（1﹣x₁）﹣¹+x₂＝1时，直线l是否总经过某一定点？若经过某一定点，求出该定点的坐标；否则，请说明理由.

查看试题解析

五、实践探究题

29. 发现：五个连续的偶数中，存在前三个偶数的平方和等于后两个偶数的平方和．
验证：

(1)、 ${(- 4)}^{2} + {(- 2)}^{2} + 0^{2} = 2^{2} + {()}^{2}$

(2)、若还存在五个连续的偶数，前三个偶数的平方和可以等于后两个偶数的平方和，设中间的偶数为n，求n

(3)、延伸：是否存在三个连续的奇数中，有前两个奇数的平方和可以等于后一个奇数的平方，请说明理由．

查看试题解析
30. 【创新是民族进步的灵魂 $！$ 华为一直在科技领域追求极致美学、极致工艺、极致创新 $.$ 真正意义上做到遥遥领先 $！$ 】我们不妨约定：若 $y_{1}$ ， $y_{2}$ 是关于 $x$ 的函数，当 $m \leq x \leq n$ 时，总有 $y_{1} - y_{2} \geq K (K > 0)$ ，并存在 $x_{0}$ 满足 $m \leq x_{0} \leq n$ ，使得 $y_{1} - y_{2} = K$ ，我们则称函数 $y_{1}$ 对 $y_{2}$ 在 $[m ， n]$ 领域“ $K$ 阶领先”．

(1)、已知一次函数 $y_{1} = - 4 x + 5$ 对 $y_{2} = 2 x - 10$ 在 $[- 2 ， 1]$ 领域“ $K$ 阶领先”，求 $K$ 的值；

(2)、已知二次函数 $y_{1} = x^{2} + 2 (t + 2) x + t^{2} (t$ 为常数 $)$ 的图象与一次函数 $y_{2} = x$ 相交于 $A$ ， $B$ 两点，其横坐标分别记为 $x_{1}$ 和 $x_{2}$ ，且满足 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - 1$ ，请判断二次函数 $y_{1}$ 对一次函数 $y_{2}$ 能否在 $[t ， t + 1]$ 领域“ $t - 2$ 阶领先”，请说明理由；

(3)、已知二次函数 $y_{1} = x^{2} + b x + c$ 的顶点经过一次函数 $y = - 4 x - 1$ 的图象，若二次函数 $y_{1} = x^{2} + b x + c$ 对一次函数 $y_{2} = - 4 x + 2$ 在 $[2 ， 3]$ 领域“ $2$ 阶领先”，求二次函数 $y_{1} = x^{2} + b x + c$ 的解析式．

查看试题解析

备考2024年中考数学核心素养专题二十 数与式的存在性问题

一、选择题

二、填空题

三、解答题

四、综合题

五、实践探究题

备考2024年中考数学核心素养专题二十数与式的存在性问题