备考2024年中考数学核心素养专题十九 圆的动态几何问题
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 如图,将半径为的圆形纸片折叠使弧经过圆心 , 过点作直径于点 , 点是半径上一动点,连接 , 则的长度不可能是( )
 A、
A、
B、
C、
D、2. 如图,矩形中, , , 点在对角线上,圆经过点 . 如果矩形有两个顶点在圆O内,那么圆O的半径长r的取值范围是( ) A、 B、 C、 D、3. 如图,△ABC中,∠ABC=90°, , D是AB中点,P是以A为圆心,以AD为半径的圆上的动点,连接PB、PC,则 的最大值为( )
A、 B、 C、 D、3. 如图,△ABC中,∠ABC=90°, , D是AB中点,P是以A为圆心,以AD为半径的圆上的动点,连接PB、PC,则 的最大值为( )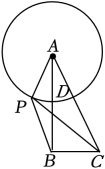 A、 B、 C、 D、4. 如图,、是的两条互相垂直的直径,点P从点O出发,沿的路线匀速运动.设(单位为度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
A、 B、 C、 D、4. 如图,、是的两条互相垂直的直径,点P从点O出发,沿的路线匀速运动.设(单位为度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )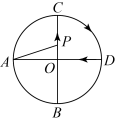 A、
A、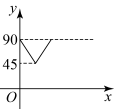 B、
B、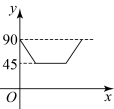 C、
C、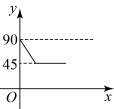 D、
D、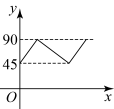 5. 如图, , , 点 , 分别在 , 的另一边上运动,并保持2,点在边上, , 点是的中点,若点为上任意一点,则的最小值为( )
5. 如图, , , 点 , 分别在 , 的另一边上运动,并保持2,点在边上, , 点是的中点,若点为上任意一点,则的最小值为( ) A、 B、 C、 D、6. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )
A、 B、 C、 D、6. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )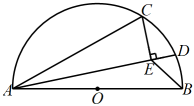 A、 B、 C、2 D、37. 如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )
A、 B、 C、2 D、37. 如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )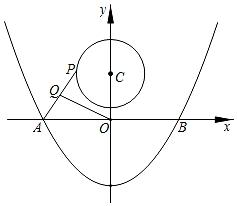 A、3 B、 C、 D、48. 如图,函数与函数的图象交于A,B两点,点P在以C(-2,0)为圆心,1为半径的圆C上,Q是AP的中点,则OQ长的最大值为( )
A、3 B、 C、 D、48. 如图,函数与函数的图象交于A,B两点,点P在以C(-2,0)为圆心,1为半径的圆C上,Q是AP的中点,则OQ长的最大值为( ) A、 B、 C、 D、9. 如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )
A、 B、 C、 D、9. 如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )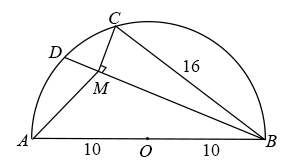 A、 B、 C、 D、10. 如图,在中, , 点O是的三等分点,半圆O与相切,M,N分别是与半圆弧上的动点,则的最小值和最大值之和是( )
A、 B、 C、 D、10. 如图,在中, , 点O是的三等分点,半圆O与相切,M,N分别是与半圆弧上的动点,则的最小值和最大值之和是( ) A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14二、填空题
-
11. 如图,抛物线y=x2﹣4x+3与y轴交于点C,与x轴交于A、B两点(A在B的左侧),点C关于抛物线对称轴的对称点为点D, 动点E在y轴上, 点F在以点B为圆心,半径为1的圆上,则DE+EF的最小值是 .
 12. 如图,在直角坐标系中,已知点、点 , 的半径为5,点C是上的动点,点P是线段的中点,那么长的取值范围是 .
12. 如图,在直角坐标系中,已知点、点 , 的半径为5,点C是上的动点,点P是线段的中点,那么长的取值范围是 .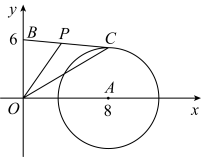 13. 如图,AB是半径为4的⊙O的弦,且AB=6,将沿着弦AB折叠,点C是折叠后的上一动点,连接并延长BC交⊙O于点D , 点E是CD的中点,连接EO , 则EO的最小值为 .
13. 如图,AB是半径为4的⊙O的弦,且AB=6,将沿着弦AB折叠,点C是折叠后的上一动点,连接并延长BC交⊙O于点D , 点E是CD的中点,连接EO , 则EO的最小值为 . 14. 如图,在等腰Rt△ABC中,AC=BC=3,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是 .
14. 如图,在等腰Rt△ABC中,AC=BC=3,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是 . 15. 如图,已知直线与x轴、y轴分别交于A、B两点,点P是以为圆心,1为半径的圆上一动点,连接 . 则面积的最大值与最小值的差为 .
15. 如图,已知直线与x轴、y轴分别交于A、B两点,点P是以为圆心,1为半径的圆上一动点,连接 . 则面积的最大值与最小值的差为 .
三、解答题
-
16. 已知:如图1,四边形ABCD内接于O,AC⊥BD于点P,F为BC延长线上一点.
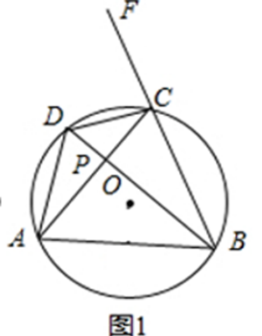
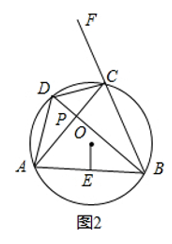
 (1)、求证:∠DCF=∠DAB(2)、过O作OE⊥AB于点E(如图2),试猜想线段OE与DC的数量关系,并证明你的猜想.(3)、当图2中点P运动到圆外时,即AC、BD的延长线交于点P,且∠P=90°时如图所示 , (2)中的猜想是否成立?如果成立请给出你的证明,如果不成立请说明理由.17. 如图所示,矩形中, , , 以点为圆心作半径的圆,交于点 , 点在线段上,过点作 , 交圆于两点 , , 连接 , 的延长线交于点 . 设().
(1)、求证:∠DCF=∠DAB(2)、过O作OE⊥AB于点E(如图2),试猜想线段OE与DC的数量关系,并证明你的猜想.(3)、当图2中点P运动到圆外时,即AC、BD的延长线交于点P,且∠P=90°时如图所示 , (2)中的猜想是否成立?如果成立请给出你的证明,如果不成立请说明理由.17. 如图所示,矩形中, , , 以点为圆心作半径的圆,交于点 , 点在线段上,过点作 , 交圆于两点 , , 连接 , 的延长线交于点 . 设(). (1)、当时,=;(2)、在从减少到的过程中,求点下降的高度;(3)、设的中点为 , 当点在线段上时,请直接写出的取值范围.18. 已知在半圆O中,直径 , 点在半圆0上运动,弦 .
(1)、当时,=;(2)、在从减少到的过程中,求点下降的高度;(3)、设的中点为 , 当点在线段上时,请直接写出的取值范围.18. 已知在半圆O中,直径 , 点在半圆0上运动,弦 . (1)、如图1,当弧与弧相等时,求证: .(2)、如图2,若 , 求图中阴影部分(弦真径、弧围成的图形)的面积;(3)、如图3,取的中点 , 点从点开始运动到点与点重合时结束,在整个运动过程中:
(1)、如图1,当弧与弧相等时,求证: .(2)、如图2,若 , 求图中阴影部分(弦真径、弧围成的图形)的面积;(3)、如图3,取的中点 , 点从点开始运动到点与点重合时结束,在整个运动过程中:①点的运动路径的总长;
②点到的距离的最小值是 .
19. 如图,AB是⊙O的直径,OA=3.动点P从点A出发, 在圆O上顺时针运动到终点B ,速度为每秒π个单位.同时动点Q从点B出发,在⊙O上沿顺时针方向运动, 速度每秒3π个单位 , 当点P到达终点时, 点Q也随之停止运动.连结OP、OQ.设点P的运动时间为t秒. (1)、⊙O的周长为 ;(2)、当点P与点Q重合时,求所在的扇形的面积;(3)、当OP⊥OQ时,求t的值;(4)、作半径OP的垂直平分线交⊙O于点M、N,连结PQ.当PQ将线段MN分成1:2的两部分时,直接写出t的值.20. 如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 .
(1)、⊙O的周长为 ;(2)、当点P与点Q重合时,求所在的扇形的面积;(3)、当OP⊥OQ时,求t的值;(4)、作半径OP的垂直平分线交⊙O于点M、N,连结PQ.当PQ将线段MN分成1:2的两部分时,直接写出t的值.20. 如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 . (1)、求 点的坐标;(2)、设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.21. 对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).
(1)、求 点的坐标;(2)、设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.21. 对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).已知在平面直角坐标系xOy中,Q(-1,0),C(1,0),⊙C的半径为r.
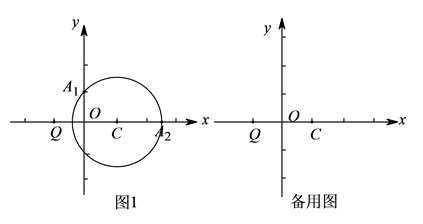 (1)、如图1,当 时,
(1)、如图1,当 时,①若A1(0,1)是⊙C的“k相关依附点”,求k的值.
②A2(1+ ,0)是否为⊙C的“2相关依附点”.
(2)、若⊙C上存在“k相关依附点”点M,①当r=1,直线QM与⊙C相切时,求k的值.
②当 时,求r的取值范围.
(3)、若存在r的值使得直线 与⊙C有公共点,且公共点时⊙C的“ 相关依附点”,直接写出b的取值范围.四、综合题
-
22. 如图1,与直线相离a,过圆心l作直线a的垂线,垂足为H,且交于P,Q两点(Q在P,H之间).我们把点P称为关于直线a的“远点”,把的值称为关于直线a的“特征数”.
图1
 图2
图2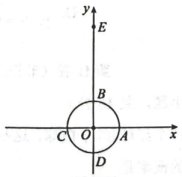 (1)、如图2,在平面直角坐标系中,点的坐标为 , 半径为1的与两坐标轴交于点A,B,C,D.
(1)、如图2,在平面直角坐标系中,点的坐标为 , 半径为1的与两坐标轴交于点A,B,C,D.①过点E作垂直于y轴的直线m,则关于直线m的“远点”是点 ▲ (填“A”,“B”,“C”或“D”),关于直线m的“特征数”为 ▲ ;
②若直线n的函数表达式为 , 求关于直线n的“特征数”;
(2)、在平面直角坐标系中,直线l经过点 , 点F是坐标平面内一点,以F为圆心,为半径作.若与直线l相离,点是关于直线l的“远点”,且关于直线l的“特征数”是 , 直接写出直线l的函数解析式.23. 如图,在平面直角坐标系中,抛物线与轴交于点 , 和点 , 直线是对称轴.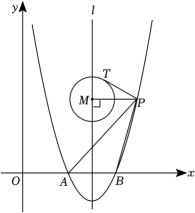 (1)、求该抛物线的函数表达式;(2)、在直线上是否存在点 , 使?若存在,求出点的坐标;若不存在,请说明理由.(3)、为第一象限内抛物线上的一个动点,且在直线右侧,连接 , , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 . 若 , 且不经过点 , 求长的取值范围.24.
(1)、求该抛物线的函数表达式;(2)、在直线上是否存在点 , 使?若存在,求出点的坐标;若不存在,请说明理由.(3)、为第一象限内抛物线上的一个动点,且在直线右侧,连接 , , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 . 若 , 且不经过点 , 求长的取值范围.24.
在平面直角坐标系中,图形上任意两点间的距离若有最大值,将这个最大值记为对于点和图形给出如下定义:点是图形上任意一点,若 , 两点间的距离有最小值,且最小值恰好为 , 则称点为图形的“关联点”(1)、如图 , 图形是矩形 , 其中点的坐标为 , 点的坐标为 , 则 ,在点 , , , 中,矩形的“关联点”是 . (2)、如图 , 图形是中心在原点的正方形 , 其中点的坐标为若直线上存在点 , 使点为正方形的“关联点”求的取值范围;
(2)、如图 , 图形是中心在原点的正方形 , 其中点的坐标为若直线上存在点 , 使点为正方形的“关联点”求的取值范围;
(3)、已知点 , 图形是以为圆心,为半径的若线段上存在点 , 使点为的“关联点“,直接写出的取值范围.25. 在平面直角坐标系中,给定圆和点 , 若过点最多可以作出条不同的直线,且这些直线被圆所截得的线段长度为正整数,则称点关于圆的特征值为已知圆的半径为 ,(1)、若点的坐标为 , 则经过点的直线被圆截得的弦长的最小值为 ,点关于圆的特征值为 ;
(2)、直线分别与 , 轴交于点 , , 若线段上总存在关于圆的特征值为的点,求的取值范围;
(3)、点是轴正半轴上一点,圆的半径为 , 点 , 分别在圆与圆上,点关于圆的特征值记为 , 点关于圆的特征值记为当点在轴正轴上运动时,若存在点 , , 使得 , 直接写出点的横坐标的取值范围.26. 在正方形中,、分别为边上的两点,连接、并延长交于点 , 连接 , 为上一点,连接、 . (1)、如图 , 若为的中点,且 , , 求线段的长;(2)、如图 , 过点作 , 且 , 连接 , 刚好交的中点 , 当时,求证:;(3)、如图 , 在的条件下,点为线段上一动点,连接 , 作于点 , 将沿翻折得到 , 点、分别为线段、上两点,且 , , 连接、交于点 , 连接 , 请直接写出面积的最大值.27. 在平面直角坐标系中,对于点 , 我们称直线为点的关联直线例如,点的关联直线为 .(1)、已知点 .
(1)、如图 , 若为的中点,且 , , 求线段的长;(2)、如图 , 过点作 , 且 , 连接 , 刚好交的中点 , 当时,求证:;(3)、如图 , 在的条件下,点为线段上一动点,连接 , 作于点 , 将沿翻折得到 , 点、分别为线段、上两点,且 , , 连接、交于点 , 连接 , 请直接写出面积的最大值.27. 在平面直角坐标系中,对于点 , 我们称直线为点的关联直线例如,点的关联直线为 .(1)、已知点 .
点的关联直线为 ;
若与点的关联直线相切,则的半径为 ;(2)、已知点 , 点点为直线上的动点.
当时,求点到点的关联直线的距离的最大值;
以为圆心,为半径作在点运动过程中,当点的关联直线与交于 , 两点时,的最小值为 , 请直接写出的值.28. 在平面直角坐标系中,对于点 , , 点与点不重合 , 给出如下定义:若 , 且 , 则称点为点关于点的“关联点”.
已知点 , 点 , 的半径为 .
(1)、在点 , , 中,是点关于点的“关联点”的为 ;
点关于点的“关联点”的坐标为 ;(2)、点为线段上的任意一点,点为线段上任意一点不与点重合 .
若上存在点关于点的“关联点”,直接写出的最大值及最小值;
当时,上不存在点关于点的“关联点”,直接写出的取值范围: .29. 如图 , 在正方形中,是边上的动点,在的外接圆上,且位于正方形的内部, , 连结 , . (1)、求证:是等腰直角三角形;(2)、如图 , 连结 , 过点作于点 , 请探究线段与的数量关系,并说明理由;(3)、当点是的中点时, .
(1)、求证:是等腰直角三角形;(2)、如图 , 连结 , 过点作于点 , 请探究线段与的数量关系,并说明理由;(3)、当点是的中点时, .①求的长;
②若点是外接圆上的动点,且位于正方形的外部,连结当与的一个内角相等时,求所有满足条件的的长.
五、实践探究题
-
30. 先阅读材料,再解答问题:
已知点 和直线 ,则点P到直线 的距离d可用公式 计算.例如:求点 到直线 的距离.
解:由直线 可知: .
所以点 到直线 的距离为 .

求:
(1)、求点P(2,-1)到直线y=x+1的距离.(2)、已知直线 与 平行,求这两条平行线之间的距离;(3)、如图已知直线 分别交 轴于 两点,☉C是以 为圆心, 为半径的圆, 为☉C上的动点,试求 面积的最大值.