备考2024年中考数学核心素养专题十六 二次函数的动态几何问题
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
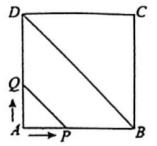
1. 如图,正方形ABCD的边长为4cm,动点P,Q同时从点A出发,以1cm/s的速度分别沿和的路径向点C运动.设运动时间为x(单位:s)四边形PBDQ的面积为y(单位:),则y与之间的函数图象大致是( )
 A、
A、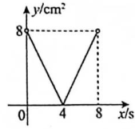 B、
B、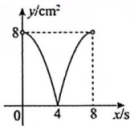 C、
C、 D、
D、 2. 某兴趣小组开展综合实践活动:在中, , 为上一点,动点以每秒1个单位的速度从点出发,在三角形边上沿匀速运动,到达点时停止,以为边作正方形 , 设点的运动时间为 , 正方形的面积为 , 当点由点运动到点时,经探究发现是关于的二次函数,并绘制成如图2所示的图象,若存在3个时刻对应的正方形DPEF的面积均相等,当时,则正方形的面积为( )
2. 某兴趣小组开展综合实践活动:在中, , 为上一点,动点以每秒1个单位的速度从点出发,在三角形边上沿匀速运动,到达点时停止,以为边作正方形 , 设点的运动时间为 , 正方形的面积为 , 当点由点运动到点时,经探究发现是关于的二次函数,并绘制成如图2所示的图象,若存在3个时刻对应的正方形DPEF的面积均相等,当时,则正方形的面积为( )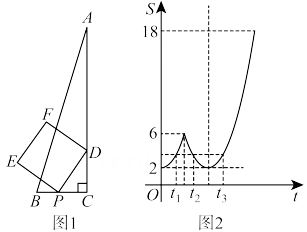 A、3 B、 C、4 D、53. 如图,抛物线与轴交于点 , 与轴的负半轴交于点 , 点是对称轴上的一个动点.连接 , 当最大时,点的坐标是( )
A、3 B、 C、4 D、53. 如图,抛物线与轴交于点 , 与轴的负半轴交于点 , 点是对称轴上的一个动点.连接 , 当最大时,点的坐标是( ) A、 B、 C、 D、4. 如图,中, , , . 点从点出发沿折线运动到点停止,过点作 , 垂足为 . 设点运动的路径长为 , 的面积为 , 若与的对应关系如图所示,则的值为( )
A、 B、 C、 D、4. 如图,中, , , . 点从点出发沿折线运动到点停止,过点作 , 垂足为 . 设点运动的路径长为 , 的面积为 , 若与的对应关系如图所示,则的值为( ) A、54 B、52 C、50 D、485. 如图,在平面直角坐标系中,抛物线与轴交于点 , 过点平行于轴的直线交抛物线于、两点,点在抛物线上且在轴的上方,连接 , 则面积的最大值是( )
A、54 B、52 C、50 D、485. 如图,在平面直角坐标系中,抛物线与轴交于点 , 过点平行于轴的直线交抛物线于、两点,点在抛物线上且在轴的上方,连接 , 则面积的最大值是( ) A、5 B、4.5 C、6 D、46. 如图,抛物线与轴交于、两点,对称轴与轴交于点 , 点 , 点 , 点是平面内一动点,且满足 , 是线段的中点,连结 . 则线段的最大值是( ).
A、5 B、4.5 C、6 D、46. 如图,抛物线与轴交于、两点,对称轴与轴交于点 , 点 , 点 , 点是平面内一动点,且满足 , 是线段的中点,连结 . 则线段的最大值是( ). A、3 B、 C、 D、57. 如图,已知抛物线经过点 , , 与y轴交于点 , P为AC上的一个动点,则有以下结论:①抛物线的对称轴为直线;②抛物线的最大值为;③;④OP的最小值为 . 则正确的结论为( )
A、3 B、 C、 D、57. 如图,已知抛物线经过点 , , 与y轴交于点 , P为AC上的一个动点,则有以下结论:①抛物线的对称轴为直线;②抛物线的最大值为;③;④OP的最小值为 . 则正确的结论为( ) A、①②④ B、①② C、①②③ D、①③④8. 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )
A、①②④ B、①② C、①②③ D、①③④8. 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )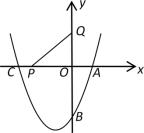 A、6 B、 C、 D、9. 如图,直线l为抛物线 的对称轴,点P为抛物线上一动点(在顶点或顶点的右侧),过点P作 轴于点A , 作PB∥x轴交抛物线于点B , 设 , ,则h与m的函数图象大致为( )
A、6 B、 C、 D、9. 如图,直线l为抛物线 的对称轴,点P为抛物线上一动点(在顶点或顶点的右侧),过点P作 轴于点A , 作PB∥x轴交抛物线于点B , 设 , ,则h与m的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动,同时点Q沿边AB,BC从点A开始向点C以2cm/s的速度移动,当点P移动到点A时,P、Q同时停止移动。设点P出发x秒时,△PAQ的面积为ycm2 , y与x的函数图象如图②,则下列四个结论,其中正确的有( )个
10. 如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动,同时点Q沿边AB,BC从点A开始向点C以2cm/s的速度移动,当点P移动到点A时,P、Q同时停止移动。设点P出发x秒时,△PAQ的面积为ycm2 , y与x的函数图象如图②,则下列四个结论,其中正确的有( )个①当点P移动到点A时,点Q移动到点C ②正方形边长为6cm ③当AP=AQ时,△PAQ面积达到最大值④线段EF所在的直线对应的函数关系式为y=−3x+18
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,在四边形ABCD中,AD∥BC , ∠DAB=30°,∠ADC=60°,BC=CD=3,若线段MN在边AD上运动,且MN=1,则AD的长为 , BM2+2BN2的最小值是.
 12. 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为 .
12. 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为 . 13. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .
13. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .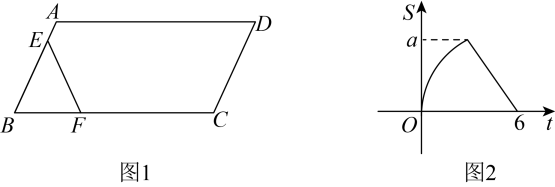 14. 抛物线的顶点D在直线上运动,顶点运动时抛物线也随之运动,抛物线与直线相交于点Q,则点Q纵坐标的最大值为.15. 一个玻璃杯竖直放置时的纵向截面如图1所示,其左右轮廓线 , 为同一抛物线的一部分, , 都与水平地面平行,当杯子装满水后 , , 液体高度 , 将杯子绕倾斜倒出部分液体,当倾斜角时停止转动,如图2所示,此时液面宽度 , 液面到点所在水平地面的距离是 .
14. 抛物线的顶点D在直线上运动,顶点运动时抛物线也随之运动,抛物线与直线相交于点Q,则点Q纵坐标的最大值为.15. 一个玻璃杯竖直放置时的纵向截面如图1所示,其左右轮廓线 , 为同一抛物线的一部分, , 都与水平地面平行,当杯子装满水后 , , 液体高度 , 将杯子绕倾斜倒出部分液体,当倾斜角时停止转动,如图2所示,此时液面宽度 , 液面到点所在水平地面的距离是 .
三、解答题
-
16. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过 , 两点,与轴的另一个交点为点 .
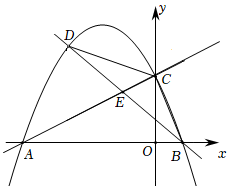 (1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.17. 如图,已知抛物线与一直线相交于 , 两点,与y轴交于点N .
(1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.17. 如图,已知抛物线与一直线相交于 , 两点,与y轴交于点N . (1)、求抛物线的函数关系式;(2)、求直线AC的函数关系式;(3)、若P是抛物线上位于直线AC上方的一个动点.求面积的最大值.18. 如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C分别在x轴的正半轴和y轴的正半轴上.抛物线y=-x2+bx+c经过A,C两点,与x轴交于另一个点D.
(1)、求抛物线的函数关系式;(2)、求直线AC的函数关系式;(3)、若P是抛物线上位于直线AC上方的一个动点.求面积的最大值.18. 如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C分别在x轴的正半轴和y轴的正半轴上.抛物线y=-x2+bx+c经过A,C两点,与x轴交于另一个点D. (1)、①求点A,B,C的坐标;
(1)、①求点A,B,C的坐标;②求b,c的值.
(2)、若点Р是边BC上的一个动点,连结AP,过点P作PM⊥AP,交y轴于点M(如图⒉所示).当点P在BC上运动时,点M也随之运动.设BP=m,CM=n,试用含m的代数式表示n,并求出n的最大值.19. 如图,在平面直角坐标系中,抛物线与轴相交于点 . (1)、求的值;(2)、点为轴上一点,其纵坐标为 , 连接 , 以为边向右作正方形 .
(1)、求的值;(2)、点为轴上一点,其纵坐标为 , 连接 , 以为边向右作正方形 .设抛物线的顶点为 , 当点在上时,求的值;
当点在抛物线上时,求的值;
当抛物线与正方形有两个交点时,直接写出的取值范围.
20. 矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为、 , 直线与BC边相交于点D . (1)、若抛物线经过D、A两点,试确定此抛物线的表达式;(2)、若以点A为圆心的与直线OD相切,试求的半径;(3)、设(1)中抛物线的对称轴与直线OD交于点M , 在对称轴上是否存在点Q , 以Q、O、M为顶点的三角形与△OCD相似.若存在,试求出符合条件的Q点的坐标;若不存在,试说明理由.21. 在平面直角坐标系中,二次函数(b、c为常数)的图象经过点和点.(1)、求这个二次函数的表达式.(2)、当时,二次函数的最大值与最小值的差为1,求的取值范围.(3)、当时,设二次函数的最大值与最小值的差为 , 求与之间的函数关系式.(4)、点在直线上运动,若在坐标平面内有且只有两个点使为直角三角形,直接写出的取值范围.
(1)、若抛物线经过D、A两点,试确定此抛物线的表达式;(2)、若以点A为圆心的与直线OD相切,试求的半径;(3)、设(1)中抛物线的对称轴与直线OD交于点M , 在对称轴上是否存在点Q , 以Q、O、M为顶点的三角形与△OCD相似.若存在,试求出符合条件的Q点的坐标;若不存在,试说明理由.21. 在平面直角坐标系中,二次函数(b、c为常数)的图象经过点和点.(1)、求这个二次函数的表达式.(2)、当时,二次函数的最大值与最小值的差为1,求的取值范围.(3)、当时,设二次函数的最大值与最小值的差为 , 求与之间的函数关系式.(4)、点在直线上运动,若在坐标平面内有且只有两个点使为直角三角形,直接写出的取值范围.四、实践探究题
-
22. 在平面直角坐标系中,抛物线y=﹣x2+bx+c(b,c是常数)与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.P为x轴上方抛物线上的动点(不与点C重合),设点P的横坐标为m.
 (1)、直接写出b,c的值;(2)、如图,直线l是抛物线的对称轴,当点P在直线l的右侧时,连接PA,过点P作PD⊥PA,交直线l于点D.若PA=PD,求m的值;(3)、过点P作x轴的平行线与直线BC交于点Q,线段PQ的长记为d.
(1)、直接写出b,c的值;(2)、如图,直线l是抛物线的对称轴,当点P在直线l的右侧时,连接PA,过点P作PD⊥PA,交直线l于点D.若PA=PD,求m的值;(3)、过点P作x轴的平行线与直线BC交于点Q,线段PQ的长记为d.①求d关于m的函数解析式;
②根据d的不同取值,试探索点P的个数情况.
23. 综合运用如图,在平面直角坐标系中,已知抛物线与轴交于、两点,与轴交于点 , 连接 .
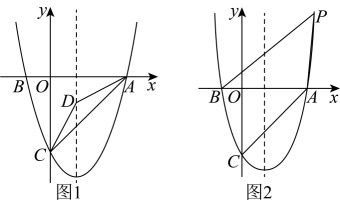 (1)、求抛物线的解析式与顶点坐标;(2)、如图1,在对称轴上是否存在一点 , 使 , 若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,若点是抛物线上的一个动点,且 , 请直接写出点的横坐标.24. 阅读下列材料:利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
(1)、求抛物线的解析式与顶点坐标;(2)、如图1,在对称轴上是否存在一点 , 使 , 若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,若点是抛物线上的一个动点,且 , 请直接写出点的横坐标.24. 阅读下列材料:利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.例题:求多项式x2﹣4x+5的最小值.
解:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,所以(x﹣2)2+1≥1.
当x=2时,(x﹣2)2+1=1.因此(x﹣2)2+1有最小值,最小值为1,即x2﹣4x+5的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:
 (1)、【理解探究】
(1)、【理解探究】已知代数式A=x2+10x+20,则A的最小值为 ;
(2)、【类比应用】张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是(3a+2)米、(2a+5)米,乙菜地的两边长分别是5a米、(a+5)米,试比较这两块菜地的面积S甲和S乙的大小,并说明理由;
(3)、【拓展升华】如图,△ABC中,∠C=90°,AC=5cm , BC=10cm , 点M、N分别是线段AC和BC上的动点,点M从A点出发以1cm/s的速度向C点运动;同时点N从C点出发以2cm/s的速度向B点运动,当其中一点到达终点时,两点同时停止运动,设运动的时间为t , 则当t的值为多少时,△MCN的面积最大,最大值为多少?
25. 探究函数的图象和性质,探究过程如下:(1)、自变量的取值范围是全体实数,与的几组对应值列表如下:其中, ▲ 根据如表数据,在图所示的平面直角坐标系中,通过描点画出了函数图象的一部分,请画出该函数图象的另一部分观察图象,写出该函数的一条性质;
(2)、点是函数图象上的一动点,点 , 点 , 当时,请直接写出所有满足条件的点的坐标;(3)、在图中,当在一切实数范围内时,抛物线交轴于 , 两点点在点的左边 , 点是点关于抛物线顶点的对称点,不平行轴的直线分别交线段 , 不含端点于 , 两点当直线与抛物线只有一个公共点时,与的和是否为定值?若是,求出此定值;若不是,请说明理由.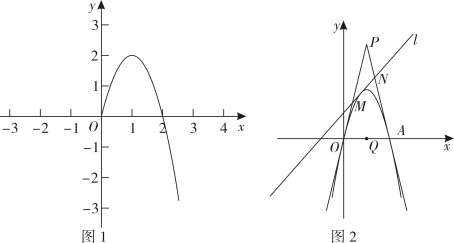 26.
26. (1)、【建立模型】如图 , 点是线段上的一点, , , , 垂足分别为 , , , . 求证:;(2)、 【类比迁移】如图 , 一次函数的图象与轴交于点、与轴交于点 , 将线段绕点逆时针旋转得到、直线交轴于点 .
(1)、【建立模型】如图 , 点是线段上的一点, , , , 垂足分别为 , , , . 求证:;(2)、 【类比迁移】如图 , 一次函数的图象与轴交于点、与轴交于点 , 将线段绕点逆时针旋转得到、直线交轴于点 .①求点的坐标;
②求直线的解析式;
(3)、【拓展延伸】如图 , 抛物线与轴交于 , 两点点在点的左侧 , 与轴交于点,已知点 , , 连接 . 抛物线上是否存在点 , 使得 , 若存在,求出点的横坐标.五、综合题
-
27. 如图注:与图完全相同 , 二次函数的图象与轴交于 , 两点,与轴交于点 .
 (1)、求该二次函数的解析式;(2)、设该抛物线的顶点为 , 求的面积请在图中探索;(3)、若点 , 同时从点出发,都以每秒个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动,当 , 运动到秒时,沿所在的直线翻折,点恰好落在抛物线上点处,请直接判定此时四边形的形状,并求出点坐标请在图中探索 .28. 如图,已知抛物线与轴交于点、点位于点的左侧 , 与轴交于点 , 轴交抛物线于点 , 为抛物线的顶点.
(1)、求该二次函数的解析式;(2)、设该抛物线的顶点为 , 求的面积请在图中探索;(3)、若点 , 同时从点出发,都以每秒个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动,当 , 运动到秒时,沿所在的直线翻折,点恰好落在抛物线上点处,请直接判定此时四边形的形状,并求出点坐标请在图中探索 .28. 如图,已知抛物线与轴交于点、点位于点的左侧 , 与轴交于点 , 轴交抛物线于点 , 为抛物线的顶点. (1)、求点、、的坐标;(2)、设动点 , 求使的值最小时的值;
(1)、求点、、的坐标;(2)、设动点 , 求使的值最小时的值;
(3)、是抛物线上一点,请你探究:是否存在点 , 使以、、为顶点的三角形与相似与不重合?若存在,求出点的坐标;若不存在,说明理由.29. 如图1,抛物线与轴交于A、B两点,与轴交于点 , 点的坐标是 , 点的坐标是 . (1)、求抛物线的解析式;(2)、如图2,点是第四象限内抛物线上一点,连接PB交轴于点 , 设点的横坐标为 , 线段CE的长为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,点是第三象限内抛物线上一点,连接PD交轴于点 , 过点作于点 , 交轴于点 , 连接AD交BP于点 , 连接MN,若 , 时,求点的坐标.30. 在平面直角坐标系中,已知抛物线与x轴分别交于 , B两点,与y轴交于点 .
(1)、求抛物线的解析式;(2)、如图2,点是第四象限内抛物线上一点,连接PB交轴于点 , 设点的横坐标为 , 线段CE的长为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,点是第三象限内抛物线上一点,连接PD交轴于点 , 过点作于点 , 交轴于点 , 连接AD交BP于点 , 连接MN,若 , 时,求点的坐标.30. 在平面直角坐标系中,已知抛物线与x轴分别交于 , B两点,与y轴交于点 . (1)、求抛物线的函数表达式;(2)、如图1,点D为第四象限抛物线上一点,连接交于点E , 求的最大值;(3)、如图2,连接 , 过点O作直线 , 点P , Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P , Q , 使 . 若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、如图1,点D为第四象限抛物线上一点,连接交于点E , 求的最大值;(3)、如图2,连接 , 过点O作直线 , 点P , Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P , Q , 使 . 若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.