备考2024年中考数学核心素养专题十五 反比例函数的动态几何问题
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y=(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A、B , 当弦AB的长等于2时,点P的坐标为( )
 A、(1,6)和(6,1) B、(2,3)和(3,2) C、( , 3)和(3 , ) D、( , 2)和(2 , )2. 已知P是反比例函数y= (x>0) 图象上一点,A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,则点P的坐标为( )
A、(1,6)和(6,1) B、(2,3)和(3,2) C、( , 3)和(3 , ) D、( , 2)和(2 , )2. 已知P是反比例函数y= (x>0) 图象上一点,A是y轴正半轴上一点,且AP⊥BP,AP:BP=1:3,则点P的坐标为( ) A、(3,4) B、(2,6) C、(6,2) D、(4,3)3. 如图,等腰△ABC的顶点A在原点固定,且始终有AC=BC,当顶点C在函数y= (x>0)的图象上从上到下运动时,顶点B在x轴的正半轴上移动,则△ABC的面积大小变化情况是( )
A、(3,4) B、(2,6) C、(6,2) D、(4,3)3. 如图,等腰△ABC的顶点A在原点固定,且始终有AC=BC,当顶点C在函数y= (x>0)的图象上从上到下运动时,顶点B在x轴的正半轴上移动,则△ABC的面积大小变化情况是( ) A、一直不变 B、先增大后减小 C、先减小后增大 D、先增大后不变4. 如图,直线交y轴于点A,交双曲线于点B,将直线向下平移2个单位长度后与y轴交于点C,交双曲线于点D,若 , 则n的值( )
A、一直不变 B、先增大后减小 C、先减小后增大 D、先增大后不变4. 如图,直线交y轴于点A,交双曲线于点B,将直线向下平移2个单位长度后与y轴交于点C,交双曲线于点D,若 , 则n的值( ) A、4 B、3 C、2 D、55. 函数y= 和y= 在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y= 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= AP.其中所有正确结论的序号是( )
A、4 B、3 C、2 D、55. 函数y= 和y= 在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y= 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= AP.其中所有正确结论的序号是( )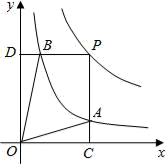 A、①②③ B、②③④ C、①③④ D、①②④6. 如图是反比例函数和(为常数)在第一象限内的图象,点M在的图象上,轴于点C,交的图象于点A,轴于点D,交的图象于点B,当点M在的图象上运动时,以下结论:①与的面积相等;②四边形的面积不变;③当点A是的中点时,则点B是的中点.其中错误结论的个数是( )
A、①②③ B、②③④ C、①③④ D、①②④6. 如图是反比例函数和(为常数)在第一象限内的图象,点M在的图象上,轴于点C,交的图象于点A,轴于点D,交的图象于点B,当点M在的图象上运动时,以下结论:①与的面积相等;②四边形的面积不变;③当点A是的中点时,则点B是的中点.其中错误结论的个数是( ) A、0 B、1 C、2 D、37. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( )
A、0 B、1 C、2 D、37. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( ) A、12 B、﹣12 C、6 D、﹣6
A、12 B、﹣12 C、6 D、﹣6二、填空题
-
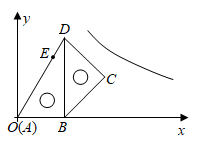
8. 将一副三角板如图放置在平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且 ,点E在AD上, ,将这副三角板整体向右平移个单位,C,E两点同时落在反比例函数 的图象上.
 9. 如图,在平面直角坐标系中, 的顶点分别为 , , ,曲线 ( ).
9. 如图,在平面直角坐标系中, 的顶点分别为 , , ,曲线 ( ).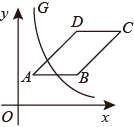 (1)、点 的坐标为 .(2)、当曲线 经过 的对角线的交点时, 的值为 .(3)、若 刚好将 边上及其内部的“整点”(横、纵坐标都为整数的点)分成数量相等的两部分,则 的取值范围是 .10. 如图,在平面直角坐标系中,已知双曲线把分成 , 两部分,且与交于点C,D,点A的坐标为 .
(1)、点 的坐标为 .(2)、当曲线 经过 的对角线的交点时, 的值为 .(3)、若 刚好将 边上及其内部的“整点”(横、纵坐标都为整数的点)分成数量相等的两部分,则 的取值范围是 .10. 如图,在平面直角坐标系中,已知双曲线把分成 , 两部分,且与交于点C,D,点A的坐标为 . (1)、连接 , 若 .
(1)、连接 , 若 .①k的值为;
②点D的坐标为;
(2)、若内(不含边界)的整点(横、纵坐标均为整数的点)与内(不含边界)的整点个数比为 , 则k的取值范围是 .11. 如图,在平面直角坐标系中,已知第一象限上的点A(m,n)是双曲线上的动点,过点A作AM∥y轴交x轴于点M,过点N(0,2n)作NB∥x轴交双曲线于点B,交直线AM于点C,若四边形OACB的面积为4,则k的值为 . 12. 如图,已知点 和点 ,点B在函数 的图像上,点C是AB的延长线上一点,过点C的直线交x轴正半轴于点E、交双曲线于点D . 如果CD=DE , 那么线段CE长度的取值范围是 .
12. 如图,已知点 和点 ,点B在函数 的图像上,点C是AB的延长线上一点,过点C的直线交x轴正半轴于点E、交双曲线于点D . 如果CD=DE , 那么线段CE长度的取值范围是 .
三、解答题
-
13. 如图,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数图象相交于A,B两点,与x轴交于点D,OB= , 且点B的横坐标是点B的纵坐标的2倍.
 (1)、求反比例函数的解析式.(2)、如图,一次函数y=kx+b的图象向下平移10个单位长度,得到新的函数图象与x轴交于点C.设点A的横坐标为m,若△ABC的面积S=15,求m的值.14. 如图所示,在平面直角坐标系中,点A是反比例函数y=(x>0)图象上一点,AB⊥x轴,垂足为B,若S△AOB=3,一次函数y=mx+2与x轴交于点C(-1,0).
(1)、求反比例函数的解析式.(2)、如图,一次函数y=kx+b的图象向下平移10个单位长度,得到新的函数图象与x轴交于点C.设点A的横坐标为m,若△ABC的面积S=15,求m的值.14. 如图所示,在平面直角坐标系中,点A是反比例函数y=(x>0)图象上一点,AB⊥x轴,垂足为B,若S△AOB=3,一次函数y=mx+2与x轴交于点C(-1,0). (1)、求k,m的值;(2)、有一点P(1,2),过点P作x轴的平行线,分别交y=mx+2和y=(x>0)的图象于点M,N.判断线段PM与PN的数量关系,并说明理由.15. 如图,在平面直角坐标系中,一次函数和反比例函数在第一象限内的图象交于点 .
(1)、求k,m的值;(2)、有一点P(1,2),过点P作x轴的平行线,分别交y=mx+2和y=(x>0)的图象于点M,N.判断线段PM与PN的数量关系,并说明理由.15. 如图,在平面直角坐标系中,一次函数和反比例函数在第一象限内的图象交于点 .
 (1)、求反比例函数的表达式;(2)、将一次函数图象向上平移后与反比例函数图象在第一象限内交于点 , 与轴交于点 , 且的面积为 , 求平移后的一次函数表达式.16. 如图,一次函数的图象经过 , 两点,与反比例函数的图象在第一象限内的交点为.
(1)、求反比例函数的表达式;(2)、将一次函数图象向上平移后与反比例函数图象在第一象限内交于点 , 与轴交于点 , 且的面积为 , 求平移后的一次函数表达式.16. 如图,一次函数的图象经过 , 两点,与反比例函数的图象在第一象限内的交点为. (1)、求一次函数和反比例函数的表达式;(2)、点是线段上一点,若 , 求点的坐标;(3)、若点是轴上一点,是否存在以点、、为顶点的三角形是等腰三角形,若存在,求出点的坐标;若不存在,说明理由.17. 如图1,一次函数的图像与y轴交于点A , 与反比例函数的图像交于点 , 连接 .
(1)、求一次函数和反比例函数的表达式;(2)、点是线段上一点,若 , 求点的坐标;(3)、若点是轴上一点,是否存在以点、、为顶点的三角形是等腰三角形,若存在,求出点的坐标;若不存在,说明理由.17. 如图1,一次函数的图像与y轴交于点A , 与反比例函数的图像交于点 , 连接 . (1)、 , .(2)、若点P在第三象限内,是否存在点P使得是以为直角边的等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.(3)、如图2,C是线段上一点(不与点A , B重合),过点C且平行于y轴的直线l交该反比例函数的图象于点D , 连接 , , . 若四边形的面积为3,求点C的坐标.18. 如图所示,抛物线与双曲线相交于点A、B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴距离的4倍,记抛物线的顶点为E。
(1)、 , .(2)、若点P在第三象限内,是否存在点P使得是以为直角边的等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.(3)、如图2,C是线段上一点(不与点A , B重合),过点C且平行于y轴的直线l交该反比例函数的图象于点D , 连接 , , . 若四边形的面积为3,求点C的坐标.18. 如图所示,抛物线与双曲线相交于点A、B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴距离的4倍,记抛物线的顶点为E。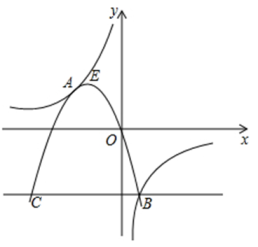 (1)、求双曲线和抛物线的函数关系式;(2)、计算△ABC与△ABE的面积;(3)、在抛物线上是否存在点D,使∆ABD的面积等于∆ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由。19. 如图,一次函数的图象与反比例函数的图象相交于点 , 与x轴交于点C,且.
(1)、求双曲线和抛物线的函数关系式;(2)、计算△ABC与△ABE的面积;(3)、在抛物线上是否存在点D,使∆ABD的面积等于∆ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由。19. 如图,一次函数的图象与反比例函数的图象相交于点 , 与x轴交于点C,且. (1)、求反比例函数与一次函数关系式;(2)、线段AC上是否存在一点D,使以点O、C、D为顶点的三角形是等腰三角形,若存在请求出D点坐标;若不存在,请说明理由.(3)、点P是x轴上一点,是否存在以点A、C、P为顶点的三角形与相似,若存在,请求出P点坐标;若不存在,请说明理由.20. 如图,正比例函数与反比例函数的图象交于点 , 点P是反比例函数图象上的一动点.过点P作轴,垂足为H , 交直线于点G .
(1)、求反比例函数与一次函数关系式;(2)、线段AC上是否存在一点D,使以点O、C、D为顶点的三角形是等腰三角形,若存在请求出D点坐标;若不存在,请说明理由.(3)、点P是x轴上一点,是否存在以点A、C、P为顶点的三角形与相似,若存在,请求出P点坐标;若不存在,请说明理由.20. 如图,正比例函数与反比例函数的图象交于点 , 点P是反比例函数图象上的一动点.过点P作轴,垂足为H , 交直线于点G .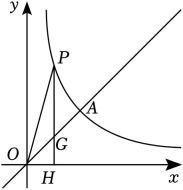 (1)、求k与m的值;(2)、若的面积是2,求此时点P的坐标.
(1)、求k与m的值;(2)、若的面积是2,求此时点P的坐标.四、综合题
-
21. 对于平面直角坐标系中的两条直线,给出如下定义:若不平行的两条直线与轴相交所成的锐角相等,则称这两条直线为“等腰三角线”如图中,若 , 则直线与直线称为“等腰三角线”;反之,若直线与直线为“等腰三角线”,则 .
 (1)、如图 , 若直线与直线为“等腰三角线”,且点、的坐标分别为、 , 求直线的解析式;(2)、如图 , 直线与双曲线交于点、 , 点是双曲线上的一个动点,点、的横坐标分别为、 , 直线、分别与轴于点、;
(1)、如图 , 若直线与直线为“等腰三角线”,且点、的坐标分别为、 , 求直线的解析式;(2)、如图 , 直线与双曲线交于点、 , 点是双曲线上的一个动点,点、的横坐标分别为、 , 直线、分别与轴于点、;求证:直线与直线为“等腰三角线”;
过点作轴的垂线 , 在直线上存在一点;连接 , 当时,求出线段的值用含的代数式表示 .
22. 如图,在平面直角坐标系中,点的坐标为 , 轴于点 , , 反比例函数的图象的一支分别交 , 于点 , , 延长交反比例函数的图象的另一支于点 , 已知点的纵坐标为 .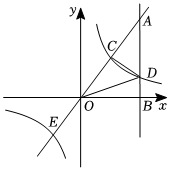 (1)、求反比例函数的表达式及点的坐标;(2)、连接 , , 求;(3)、在轴上是否存在两点 , 在的左侧 , 使以 , , , 为顶点的四边形为矩形?若存在,求出矩形的周长;若不存在,说明理由.23. 如图1,反比例函数与一次函数的图象交于两点,已知 .
(1)、求反比例函数的表达式及点的坐标;(2)、连接 , , 求;(3)、在轴上是否存在两点 , 在的左侧 , 使以 , , , 为顶点的四边形为矩形?若存在,求出矩形的周长;若不存在,说明理由.23. 如图1,反比例函数与一次函数的图象交于两点,已知 . (1)、求反比例函数和一次函数的表达式;(2)、一次函数的图象与轴交于点 , 点(未在图中画出)是反比例函数图象上的一个动点,若 , 求点的坐标:(3)、若点是坐标轴上一点,点是平面内一点,是否存在点 , 使得四边形是矩形?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.24. 如图,一次函数的图像与反比例函数的图像交于 , 两点.( , , 为常数)
(1)、求反比例函数和一次函数的表达式;(2)、一次函数的图象与轴交于点 , 点(未在图中画出)是反比例函数图象上的一个动点,若 , 求点的坐标:(3)、若点是坐标轴上一点,点是平面内一点,是否存在点 , 使得四边形是矩形?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.24. 如图,一次函数的图像与反比例函数的图像交于 , 两点.( , , 为常数) (1)、求一次函数和反比例函数的解析式;(2)、将一次函数向下平移个单位后与反比例函数的图像有且只有一个公共点,求的值;(3)、为轴上一点,若的面积为 , 求点的坐标.25. 已知,矩形OCBA在平面直角坐标系中的位置如图所示,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B坐标为(3,6),反比例函数的图象经过AB的中点D , 且与BC交于点E , 顺次连接O , D , E .
(1)、求一次函数和反比例函数的解析式;(2)、将一次函数向下平移个单位后与反比例函数的图像有且只有一个公共点,求的值;(3)、为轴上一点,若的面积为 , 求点的坐标.25. 已知,矩形OCBA在平面直角坐标系中的位置如图所示,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B坐标为(3,6),反比例函数的图象经过AB的中点D , 且与BC交于点E , 顺次连接O , D , E . (1)、求m的值及点E的坐标;(2)、点M为y轴正半轴上一点,若△MBO的面积等于△ODE的面积,求点M的坐标;(3)、平面直角坐标系中是否存在一点N , 使得O , D , E , N四点顺次连接构成平行四边形?若存在,请直接写出N的坐标;若不存在,请说明理由.26. 如图,点、是一次函数与反比例函数图象的交点,点在轴上运动,请结合图象解决下列问题:
(1)、求m的值及点E的坐标;(2)、点M为y轴正半轴上一点,若△MBO的面积等于△ODE的面积,求点M的坐标;(3)、平面直角坐标系中是否存在一点N , 使得O , D , E , N四点顺次连接构成平行四边形?若存在,请直接写出N的坐标;若不存在,请说明理由.26. 如图,点、是一次函数与反比例函数图象的交点,点在轴上运动,请结合图象解决下列问题: (1)、求点、的坐标及的面积;(2)、根据图象直接写出当取什么值时,?(3)、点在轴上运动的过程中,
(1)、求点、的坐标及的面积;(2)、根据图象直接写出当取什么值时,?(3)、点在轴上运动的过程中,①直接写出的最小值: .
②的面积是否发生变化,如果变化,请说明理由;如果不变化,请求出的面积.
27. 如图,在平面直角坐标系中,矩形的顶点B的坐标为 , , 分别落在x轴和y轴上,将绕点O逆时针旋转,使点B落在y轴上,得到 , 与相交于点F,反比例函数的图象经过点F,交于点G. (1)、求k的值;(2)、若点P在坐标轴上运动,求动点P的坐标,使 .28. 如图,一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,与y轴交于点C,轴于点D, , 点C关于直线的对称点为点E.
(1)、求k的值;(2)、若点P在坐标轴上运动,求动点P的坐标,使 .28. 如图,一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,与y轴交于点C,轴于点D, , 点C关于直线的对称点为点E.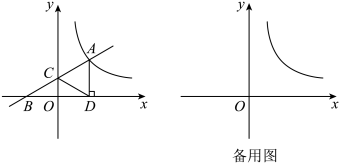 (1)、点E是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.点P在y轴上,当最大时,求点P的坐标.29. 如图,一次函数()的图像与轴交于点 , 与反比例函数()的图像交于点 .
(1)、点E是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.点P在y轴上,当最大时,求点P的坐标.29. 如图,一次函数()的图像与轴交于点 , 与反比例函数()的图像交于点 .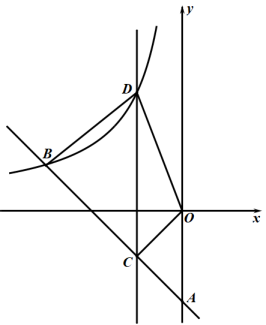
 (1)、b=;k=;(2)、点是线段上一点(不与重合),过点且平行于轴的直线交该反比例函数的图象于点 , 连接 , 若四边形的面积 , 求点的坐标;(3)、将第(2)小题中的沿射线方向平移一定的距离后,得到 , 若点 的对应点恰好落在该反比例函数图象上(如图),求此时点的对应点的坐标.
(1)、b=;k=;(2)、点是线段上一点(不与重合),过点且平行于轴的直线交该反比例函数的图象于点 , 连接 , 若四边形的面积 , 求点的坐标;(3)、将第(2)小题中的沿射线方向平移一定的距离后,得到 , 若点 的对应点恰好落在该反比例函数图象上(如图),求此时点的对应点的坐标.五、实践探究题
-
30. 综合与探究
如图1,在平面直角坐标系中,菱形的顶点在轴上,反比例函数()的图象经过点 , 并与线段交于点 , 反比例函数()的图象经过点 , 交轴于点 . 已知 .
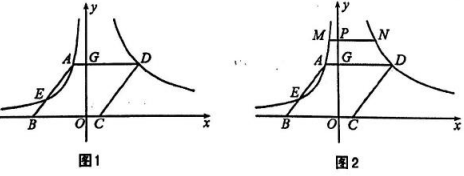 (1)、求点的坐标及反比例函数()的表达式;(2)、直接写出点的坐标 ;(3)、如图2,点是轴正半轴上的一个动点,过点作轴的垂线,分别交反比例函数()与反比例函数()的图象于点 , 设点的坐标为
(1)、求点的坐标及反比例函数()的表达式;(2)、直接写出点的坐标 ;(3)、如图2,点是轴正半轴上的一个动点,过点作轴的垂线,分别交反比例函数()与反比例函数()的图象于点 , 设点的坐标为①当时,求的值;
②在点运动过程中,是否存在某一时刻,使?若存在,直接写出点的坐标;若不存在,说明理由.