备考2024年中考数学核心素养专题十三 定值问题
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 如果a,b为定值时,关于x的方程=1,无论k为何值时,它的根总是2,则a+b的值为( )A、18 B、15 C、12 D、102. 如图,把一个周长为定值的长方形分割为五个四边形,其中是正方形, , , , 都是长方形,这五个四边形的周长分别用 , , , , 表示,则下列各式的值为定值的是( )
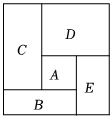 A、 B、 C、 D、3. 如图,长为 , 宽为的大长方形被分割为小块,除阴影 , 外,其余块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的有( )
A、 B、 C、 D、3. 如图,长为 , 宽为的大长方形被分割为小块,除阴影 , 外,其余块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的有( )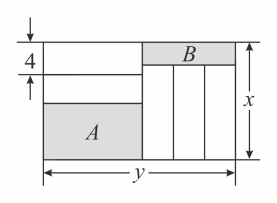
小长方形的较长边为;
阴影的较短边和阴影的较短边之和为;
若为定值,则阴影和阴影的周长和为定值;
当时,阴影和阴影的面积和为定值.
A、个 B、个 C、个 D、个4. 如图,在边长为的正方形中,是对角线上一点,且 , 点是上一动点,则点到边 , 的距离之和的值( ) A、是定值 B、是定值 C、有最小值 D、有最大值5. 如图,在线段的延长线上, , , , 连接交于点 , 的余角比大 , 为线段上一点,连接 , , 使 , 在内部有射线 , 平分 , 则下列结论:;平分;;的角度为定值且定值为 , 其中正确结论的个数有( )
A、是定值 B、是定值 C、有最小值 D、有最大值5. 如图,在线段的延长线上, , , , 连接交于点 , 的余角比大 , 为线段上一点,连接 , , 使 , 在内部有射线 , 平分 , 则下列结论:;平分;;的角度为定值且定值为 , 其中正确结论的个数有( ) A、个 B、个 C、个 D、个6. 如图,在第一象限内,点A是一次函数图象上一动点,点B,C的坐标分别是 , , 若反比例函数和的图象分别经过点A,D,则下列代数式的值为定值的是( )
A、个 B、个 C、个 D、个6. 如图,在第一象限内,点A是一次函数图象上一动点,点B,C的坐标分别是 , , 若反比例函数和的图象分别经过点A,D,则下列代数式的值为定值的是( ) A、 B、 C、 D、7. 如图,在等腰Rt△ABC中,∠C=90°,AC=6,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE的面积是定值9;③△DFE的面积最小值为4.5;④DE长度的最小值为3.其中正确的结论是( )
A、 B、 C、 D、7. 如图,在等腰Rt△ABC中,∠C=90°,AC=6,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE的面积是定值9;③△DFE的面积最小值为4.5;④DE长度的最小值为3.其中正确的结论是( ) A、①②③ B、①②④ C、①③④ D、②③④8. 如图,正方形的边长为4,G是对角线上一动点,于点 , 于点 , 连接 , 给出四种情况:
A、①②③ B、①②④ C、①③④ D、②③④8. 如图,正方形的边长为4,G是对角线上一动点,于点 , 于点 , 连接 , 给出四种情况:①若G为的中点,则四边形是正方形;②若G为上任意一点,则;③点G在运动过程中,的值为定值4;④点G在运动过程中,线段的最小值为 .
 A、①②③④ B、①②③ C、①②④ D、①③④9. 如图,在边长为a的正方形中,E是对角线上一点,且 , 点P是上一动点,则点P到边 , 的距离之和的值( )
A、①②③④ B、①②③ C、①②④ D、①③④9. 如图,在边长为a的正方形中,E是对角线上一点,且 , 点P是上一动点,则点P到边 , 的距离之和的值( ) A、有最大值a B、有最小值 C、是定值a D、是定值10. 已知无论 , 取什么值,多项式的值都等于定值12,则等于( ).A、8 B、 C、2 D、11. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )
A、有最大值a B、有最小值 C、是定值a D、是定值10. 已知无论 , 取什么值,多项式的值都等于定值12,则等于( ).A、8 B、 C、2 D、11. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )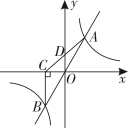 A、1个 B、2个 C、3个 D、4个12. 如图,在菱形中, , 点E,F分别是边上任意点(不与端点重合),且 , 连接相交于点G,连接与相交于点H,下列结论:①;②的大小为定值;③与一定不垂直;④若 , 则 , 其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个12. 如图,在菱形中, , 点E,F分别是边上任意点(不与端点重合),且 , 连接相交于点G,连接与相交于点H,下列结论:①;②的大小为定值;③与一定不垂直;④若 , 则 , 其中正确的结论有( ) A、①② B、①②④ C、③④ D、①③④
A、①② B、①②④ C、③④ D、①③④二、填空题
-
13. 在平面直角坐标系xOy中,P , Q是函数图象上异于A(1,1)的点,直线PQ与直线y=x垂直,分别交x轴,y轴于点M , N . 现给出以下结论:
①MP=NQ;
②∠PAQ可能是直角;
③MN2﹣PQ2为定值;
④△MON的面积可能为2.
其中正确的是 . (写出所有正确结论的序号)
14. 已知关于x,y的方程组 , 无论k取何值,的值都是一个定值,则这个定值为 .15. 若、为定值,关于的一次方程无论为何值时,它的解总是 , 则的值为 .16. 已知关于x,y的二元一次方程组有下列说法:①当x与y相等时,解得;②当x与y互为相反数时,解得;③若 , 则;④无论k为何值,x与y的值一定满足关系式 , 其中正确的序号是 .17. 如图,点为定角的平分线上的一个定点,且与互补,若在绕点旋转的过程中,其两边分别与、相交于、两点,则以下结论:①恒成立;②的值不变;③四边形的面积不变;④的长不变,其中正确的序号为 . 18. 如图,小明在计算机上用“几何画板”画了一个Rt△ABC,∠C=90°,并画出了两锐角的角平分线AD, BE及其交点F.小明发现,无论怎祥变动Rt△ABC的形状和大小,∠AFB的度数是定值.这个定值为 .
18. 如图,小明在计算机上用“几何画板”画了一个Rt△ABC,∠C=90°,并画出了两锐角的角平分线AD, BE及其交点F.小明发现,无论怎祥变动Rt△ABC的形状和大小,∠AFB的度数是定值.这个定值为 . 19. 如图,边长为1的正方形中,点E为边上动点(不与A、D重合),连接 , 将沿折叠得到 , 延长交于点F,连接 , 交于点N,连接 . 则下列结论:①;②的周长是定值2;③当点E是中点时,;④点D到距离的最大值为 , 其中正确的结论有(填写所有正确结论的序号).
19. 如图,边长为1的正方形中,点E为边上动点(不与A、D重合),连接 , 将沿折叠得到 , 延长交于点F,连接 , 交于点N,连接 . 则下列结论:①;②的周长是定值2;③当点E是中点时,;④点D到距离的最大值为 , 其中正确的结论有(填写所有正确结论的序号).
三、综合题
-
20. 项目化成果展示了一款简易电子秤:可变电阻上装有托盘(质量忽略不计),测得物品质量x(kg)与可变电阻y(Ω)的多组对应值,画出函数图象(如图1).图2是三种测量方案,电源电压恒为8V,定值电阻为30Ω,与可变电阻串联.

【链接】串联电路中,通过两个电阻的电流I相等,.可变电阻、定值电阻两端的电压之和为8V,则有.
(1)、求y关于x的函数表达式,并写出自变量x的取值范围.(2)、三个托盘放置不同物品后,电表A, , 的读数分别为0.1A,6V,4V.请从以下方案中选择一个,求出对应物品的质量是多少kg?(3)、小明家买了某散装大米65kg,为了检验商家是否存在缺斤少两的情况,请你将大米分批称重,用方案一、二、三来进行检验,设大米为 , 前两次称合适的千克数,第3次用含a的代数式表示,请填写下表.第1次(方案一)
第2次(方案二)
第3次(方案三)
大米(kg)
读数
I= A
= V
V
21. 在面积为定值的一组矩形中,当矩形的一条边长为7.5 cm时,它的邻边长为8 cm.(1)、设矩形相邻的两条边长分别为x cm,y cm,求y关于x的函数解析式.这个函数是反比例函数吗?(2)、若其中一个矩形的一条边长为5 cm,求这个矩形与之相邻的另一条边长.22. 已知代数式 , 先用配再求出当x取何值时,这个代数式的值最小,最小值是多少?方法说明,不论x取何值,这个代数式的值总是正数.23. 定义:若n为常数,当一个函数图象上存在横、纵坐标和为n的点,则称该点为这个函数图象关于n的“恒值点”,例如:点(1,2)是函数图象关于3的“恒值点”. (1)、判断点(1,3),(2,8),(3,7)是否为函数图象关于10的“恒值点”.(2)、如图1,抛物线与x轴交于A,B两点(A在B的左侧),现将抛物线在x轴下方的部分沿x轴翻折,抛物线的其余部分保持不变,所得的新图象如图2所示.
(1)、判断点(1,3),(2,8),(3,7)是否为函数图象关于10的“恒值点”.(2)、如图1,抛物线与x轴交于A,B两点(A在B的左侧),现将抛物线在x轴下方的部分沿x轴翻折,抛物线的其余部分保持不变,所得的新图象如图2所示.Ⅰ.求翻折后A,B之间的抛物线解析式.(不必写出x的取值范围)
Ⅱ.当新图象上恰好有3个关于c的“恒值点”时,请用含b的代数式表示c.
24. 对于某一函数给出如下定义:如果存在实数p , 当其自变量的值为p时,其函数值等于p , 则称p为这个函数的不动值,在函数存在不动值时,该函数的最大不动值与最小不动值之差q称为这个函数的不动长度,特别地,当函数只有一个不动值时,其不动长度q为0,例如,下图中的函数有0和1两个不动值,其不动长度q为1. (1)、下列函数①y=2x , ②y=x2+1,③y=x2﹣2x中存在不动值的是 (填序号)(2)、函数y=3x2+bx ,
(1)、下列函数①y=2x , ②y=x2+1,③y=x2﹣2x中存在不动值的是 (填序号)(2)、函数y=3x2+bx ,①若其不动长度为0,则b的值为 ;
②若﹣2≤b≤2,求其不动长度q的取值范围;
(3)、记函数y=x2﹣4x(x≥t)的图象为G1 , 将G1沿x=t翻折后得到的函数图象记为G2 , 函数G的图象由G1和G2两部分组成,若其不动长度q满足0≤q≤5,则t的取值范围为 .25. 在平面直角坐标系中,我们不妨把纵坐标的值与横坐标的值的平方相等的点称为“雅心点”,例如点( , 1),(0,0),( , 2),…都是“雅心点”,显然,这样的“雅心点”有无数个.(1)、求一次函数上的所有“雅心点”的坐标为;(2)、若过点(1,)的直线上恰好只有一个“雅心点”,请求出符合要求的直线解析式;(3)、若二次函数(a是常数,a>0)的图象上存在两个不同的“雅心点”,且“雅心点”的横坐标的值都不大于2,试求实数a的取值范围.26. 我们规定,对于已知线段AB,若存在动点C(点C不与点A,B重合)始终满足∠ACB的大小为定值,则称△ABC是“立信三角形”,其中AB的长称为它的“立信长”,∠ACB称为它的“立信角”. (1)、如图(1),已知立信△ABC中“立信长” , “立信角” , 请直接写出立信△ABC面积的最大值;(2)、如图(2),在△ABD中, , , C是立信△ABC所在平面上的一个动点,且立信角 , 求立信△ABC面积的最大值;(3)、如图(3),已知立信长(a是常数且),点C是平面内一动点且满足立信角 , 若∠ABC,∠BAC的平分线交于点D,问:点D的运动轨迹长度是否为定值?如果是,请求出它的轨迹长度;如果不是,请说明理由.27. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.
(1)、如图(1),已知立信△ABC中“立信长” , “立信角” , 请直接写出立信△ABC面积的最大值;(2)、如图(2),在△ABD中, , , C是立信△ABC所在平面上的一个动点,且立信角 , 求立信△ABC面积的最大值;(3)、如图(3),已知立信长(a是常数且),点C是平面内一动点且满足立信角 , 若∠ABC,∠BAC的平分线交于点D,问:点D的运动轨迹长度是否为定值?如果是,请求出它的轨迹长度;如果不是,请说明理由.27. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.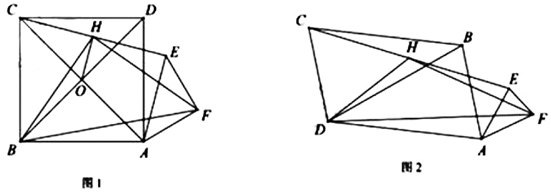 (1)、① ▲ ;
(1)、① ▲ ;② ▲ .
③小明为了证明①②,连接 交 于O , 连接 ,证明了 和 的关系,请你按他的思路证明①②.
(2)、小明又用三个相似三角形(两个大三角形全等)摆出如图2, , ( )求① (用k的代数式表示)
② (用k、 的代数式表示)
28. 探究活动一: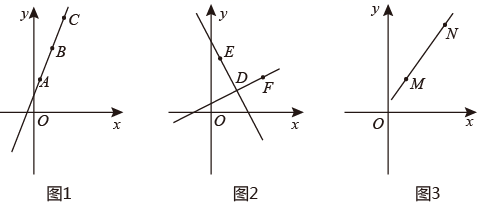
如图1,某数学兴趣小组在研究直线上点的坐标规律时,发现在直线 上的三点 , , ,有 , , ,兴趣小组提出猜想:若直线 上任意两点 , ,则 是定值.通过多次验证和查阅资料得知,猜想成立, 是定值,并且是直线 中的 ,叫做这条直线的斜率.
(1)、请你应用以上规律直接写出过 , 两点的直线 的斜率 .(2)、探究活动二: 数学兴趣小组继续深入研究直线的“斜率”问题,得到正确结论:当任意两条不和坐标轴平行的直线互相垂直时,这两条直线的斜率之积是定值.
如图2,直线 与直线 垂直于点 ,且 , , .请求出直线 与直线 的斜率之积.并写出你发现的结论.(3)、综合应用:
如图3, , ,请结合探究活动二的结论,求出过点 且与直线 垂直的直线的解析式.29. 跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K为飞行距离计分的参照点,落地点超过点K越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA为66m,基准点K到起跳台的水平距离为75m,高度为h(m)(为定值).设运动员从起跳点A起跳后的高度y(m)与水平距离之间的函数关系式为y=ax2+bx+c(a≠0).
(1)、的值为.(2)、若运动员落地点恰好到达点,且此时 , 求基准点的高度.(3)、若时,运动员落地点要超过点 , 则的取值范围是.(4)、若运动员飞行的水平距离为时,恰好达到最大高度 , 试判断他的落地点能否超过点 , 并说明理由.四、实践探究题
-
30. 【问题】探究一次函数y=kx+k+1(k≠0)图象特点.

【探究】可做如下尝试:
y=kx+k+1=k(x+1)+1,当x=﹣1时,可以消去k,求出y=1.
【发现】结合一次函数图象,发现无论k取何值,一次函数y=kx+k+1的图象一定经过一个固定的点,该点的坐标是 ▲ ;
【应用】一次函数y=(k+2)x+k的图象经过定点P.
①点P的坐标是 ▲ ;
②已知一次函数y=(k+2)x+k的图象与y轴相交于点A,若△OAP的面积为3,求k的值.
31. 阅读材料:对于两个正数a、b,则 (当且仅当a=b时取等号).
当 为定值时, 有最小值;当 为定值时, 有最大值.
例如:已知 ,若 ,求 的最小值.
解:由 ≥ ,得 ≥ ,当且仅当 即 时, 有最小值,最小值为 .
根据上面的阅读材料回答下列问题:
(1)、已知 ,若 ,则当 时, 有最小值,最小值为;(2)、已知 ,若 ,则 取何值时, 有最小值,最小值是多少?(3)、用长为 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?32. (发现问题)小明在学习过程中发现:周长为定值的矩形中面积最大的是正方形.那么,面积为定值的矩形中,其周长的取值范围如何呢?
(解决问题)
小明尝试从函数图象的角度进行探究:
(1)、建立函数模型设一矩形的面积为4,周长为m,相邻的两边长为x、y,则x y=4,2(x+y)=m,
即 , ,那么满足要求的(x,y)应该是函数 与 的图象在第象限内的公共点坐标.
(2)、画出函数图象①画函数 (x>0)的图象;
②在同一直角坐标系中直接画出 的图象,则 的图象可以看成是由 的图象向右平移 ▲ 个单位长度得到.
(3)、研究函数图象:平移直线 ,观察两函数的图象;①当直线平移到与函数 (x>0)的图象有唯一公共点的位置时,公共点的坐标为 ▲ ,周长m的值为 ▲ ;
②在直线平移的过程中,两函数图象公共点的个数还有什么情况?请直接写出公共点的个数及对应周长m的取值范围.
(4)、(结论运用)面积为10的矩形的周长m的取值范围为.33. 对于任意正实数, , , ,只有 时,等号成立.结论:在 (,均为正实数)中,若为定值,则 ,只有当 时,a+b有最小值 .根据上述内容,回答下列问题:(1)、初步探究:若 ,只有当 时,有 最小值;(2)、深入思考:下面一组图是由4个全等的矩形围成的大正方形,中空部分是小正方形,矩形的长和宽分别为,试利用大正方形与四个矩形的面积的大小关系,验证 ,并指出等号成立时的条件; (3)、拓展延伸:如图,已知 , ,点是第一象限内的一个动点,过点向坐标轴作垂线,分别交轴和轴于,两点,矩形的面积始终为48,求四边形面积的最小值以及此时点的坐标.
(3)、拓展延伸:如图,已知 , ,点是第一象限内的一个动点,过点向坐标轴作垂线,分别交轴和轴于,两点,矩形的面积始终为48,求四边形面积的最小值以及此时点的坐标.