备考2024年中考数学探究性训练专题28 图形与坐标的性质
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中箭头方向排列,如 , , , , , , , , 根据规律探索可得,第31个点的坐标为( )
 A、 B、 C、 D、2. 如下图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,O),(3,-l),…,根据技个规律探索可得,第100个点的坐标为( )
A、 B、 C、 D、2. 如下图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,O),(3,-l),…,根据技个规律探索可得,第100个点的坐标为( ) A、(14,0) B、(14,-1) C、(14,1) D、(14,2)3. 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 , , ,…得到斐波那契螺旋线,然后顺次连结P1P2 , P2P3 , P3P4 , …得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上的点P9的坐标为( )
A、(14,0) B、(14,-1) C、(14,1) D、(14,2)3. 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 , , ,…得到斐波那契螺旋线,然后顺次连结P1P2 , P2P3 , P3P4 , …得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上的点P9的坐标为( ) A、(﹣6,24) B、(﹣6,25) C、(﹣5,24) D、(﹣5,25)4. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),……,根据这个规律探索可得第2023个点的坐标是( )
A、(﹣6,24) B、(﹣6,25) C、(﹣5,24) D、(﹣5,25)4. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),……,根据这个规律探索可得第2023个点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
5. 教材在第七章复习题的“拓广探索”中,曾让同学们探索发现:在平面直角坐标系中,线段中点的横坐标(纵坐标)分别等于对应线段的两个端点的横坐标(纵坐标)和的一半,例如:点 , 点 , 则线段的中点的坐标为 , 请利用以上结论解决问题:在平面直角坐标系中,点 , 若线段的中点恰好在轴上,且到轴的距离是 , 则 .6. 如图,在平面直角坐标系中,点 , , , 根据这个规律,探究可得点的坐标是 .
 7. 教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,有两点、 , 所连线段的中点是M,则M的坐标为 , 如:点、点 , 则线段AB的中点M的坐标为 , 即.利用以上结论解决问题:平面直角坐标系中,若 , , 线段的中点G恰好位于y轴上,且到x轴的距离是1,则的值等于.8. 如图,线段AB两端点坐标分别为 ,线段CD两端点坐标分别为 、D 数学课外兴趣小组研究这两线段发现:其中一条线段绕着某点旋转一个角度可得到另一条线段,请写出旋转中心的坐标 .
7. 教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,有两点、 , 所连线段的中点是M,则M的坐标为 , 如:点、点 , 则线段AB的中点M的坐标为 , 即.利用以上结论解决问题:平面直角坐标系中,若 , , 线段的中点G恰好位于y轴上,且到x轴的距离是1,则的值等于.8. 如图,线段AB两端点坐标分别为 ,线段CD两端点坐标分别为 、D 数学课外兴趣小组研究这两线段发现:其中一条线段绕着某点旋转一个角度可得到另一条线段,请写出旋转中心的坐标 .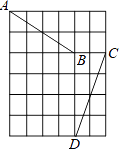 9. 在平面直角坐标系xOy中,已知直线l:y=x , 作A1(1,0)关于y=x的对称点B1 , 将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2 , 将点B2向右水平平移2个单位得到点A3;….请继续操作并探究:点A3的坐标是 , 点B2014的坐标是 .10. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37)….如果单独把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对:.
9. 在平面直角坐标系xOy中,已知直线l:y=x , 作A1(1,0)关于y=x的对称点B1 , 将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2 , 将点B2向右水平平移2个单位得到点A3;….请继续操作并探究:点A3的坐标是 , 点B2014的坐标是 .10. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37)….如果单独把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对:.
三、理论探究题
-
11. 定义:在平面直角坐标系中,对于任意两点 , , 若点满足 , , 那么称点是点和的衍生点.例如: , , 则点是点和的衍生点.已知点 , 点 , 点是点和的衍生点.(1)、若点 , 则点的坐标为(2)、请直接写出点的坐标(用表示);(3)、若直线交轴于点 , 当时,求点的坐标.12. 在平面直角坐标系中,对于点 , 若点的坐标为 , 其中 为常数,对称点是点的“级关联点”,例如:点的“2级关联点” , 即.(1)、已知点的:“3级关联点”为 , 求点的坐标;(2)、已知点关于“2级关联点”为 , 求的坐标;(3)、点关于-4级关联点在第三象限,求的范围。13. 如图,直线与轴分别交于 , , 点坐标为 , 点的坐标为 , , 是直线上的一个动点.
 (1)、求的值;(2)、当点在第二象限内运动过程中,试写出三角形的面积与的函数关系式,并写出自变量的取值范围;(3)、探究:当运动到什么位置时,三角形的面积为 , 并说明理由.14. 阅读:在平面直角坐标系中,已知两点的坐标,可构造直角三角形,运用勾股定理,求这两点间的距离;在平面直角坐标系中有两点 , , 求 , 两点间的距离过点作轴的垂线,过点作轴的垂线,相交于点 , 连接 , , 在中,由勾股定理得: , 若 , , 从而得到两点间的距离公式解决下列问题:
(1)、求的值;(2)、当点在第二象限内运动过程中,试写出三角形的面积与的函数关系式,并写出自变量的取值范围;(3)、探究:当运动到什么位置时,三角形的面积为 , 并说明理由.14. 阅读:在平面直角坐标系中,已知两点的坐标,可构造直角三角形,运用勾股定理,求这两点间的距离;在平面直角坐标系中有两点 , , 求 , 两点间的距离过点作轴的垂线,过点作轴的垂线,相交于点 , 连接 , , 在中,由勾股定理得: , 若 , , 从而得到两点间的距离公式解决下列问题: (1)、若 , , 则两点间的距离 ;(2)、如图:点 , 点 , 则 ,若 , 则 .15. 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
(1)、若 , , 则两点间的距离 ;(2)、如图:点 , 点 , 则 ,若 , 则 .15. 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形. (1)、点C的坐标是 , △ABC的面积是;(2)、将△ABC绕点C旋转180°得到△A1B1C1 , 连接AB1、BA1 , 画出四边形AB1A1B,并判断四边形AB1A1B是何种特殊四边形 ▲ ;(3)、请探究:在x轴上是否存在这样的点P,使四边形ABOP的面积等于△ABC面积的2倍?若存在,请直接写出点P的坐标(不必写出解答过程);若不存在,请说明理由.16. 在平面直角坐标系中,若点的坐标满足 , 则我们称点N为“健康点”;若点的坐标满足 , 则我们称Q为“快乐点”.
(1)、点C的坐标是 , △ABC的面积是;(2)、将△ABC绕点C旋转180°得到△A1B1C1 , 连接AB1、BA1 , 画出四边形AB1A1B,并判断四边形AB1A1B是何种特殊四边形 ▲ ;(3)、请探究:在x轴上是否存在这样的点P,使四边形ABOP的面积等于△ABC面积的2倍?若存在,请直接写出点P的坐标(不必写出解答过程);若不存在,请说明理由.16. 在平面直角坐标系中,若点的坐标满足 , 则我们称点N为“健康点”;若点的坐标满足 , 则我们称Q为“快乐点”. (1)、若点是“健康点”,则点A的坐标为 .(2)、在(1)的条件下,若点B是x轴上的“健康点”,点C是y轴上的“快乐点”,如果P为x轴上一点,且与面积相等,求点P的坐标.17. 如图,在平面直角坐标系中, , , 过点作直线轴,点是直线上的动点,以为边在右上侧作等腰直角 , 使 .
(1)、若点是“健康点”,则点A的坐标为 .(2)、在(1)的条件下,若点B是x轴上的“健康点”,点C是y轴上的“快乐点”,如果P为x轴上一点,且与面积相等,求点P的坐标.17. 如图,在平面直角坐标系中, , , 过点作直线轴,点是直线上的动点,以为边在右上侧作等腰直角 , 使 . (1)、如图1当点落在点时,则点的坐标是;(2)、学生甲认为点的坐标一定跟点有关,于是进行了如下探究:
(1)、如图1当点落在点时,则点的坐标是;(2)、学生甲认为点的坐标一定跟点有关,于是进行了如下探究:如图2,小聪同学画草图时,让点落在、、不同的特殊位置时(在轴上、与轴平行、当落在轴上时对应点),画出了几个点对应的、、三个不同的位置,发现、、在同一条直线上,请你根据学生甲的猜测及题目条件,求出点所在直线的解析式;
(3)、在(2)中,虽然求出了点所在直线的解析式,但是小明同学认为几个特殊点确定解析式是一种猜测,当点在上运动时,所有的点都在一条直线上吗?就解设了点的坐标为 , 希望用一般推理的方式求出和满足的关系式,请你帮助小明给出解答.18. 在平面直角坐标系中,对于 , 两点给出如下定义:若点的横纵坐标的绝对值之和等于点的横纵坐标的绝对值之和,则称 , 两点为“等和点”下图中的 , 两点即为“等和点”.
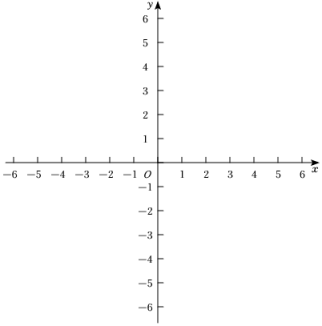 (1)、已知点的坐标为 ,
(1)、已知点的坐标为 ,在点 , , 中,与点为“等和点”的是只填字母;
若点在第一象限的角平分线上,且 , 两点为“等和点”,则点的坐标为 ;
(2)、已知点的坐标为 , 点的坐标为 , 连接 , 点为线段上一点,过点作轴的垂线 , 若垂线上存在点的“等和点”,求的取值范围.19. 我们约定,在平面直角坐标系中,对于不同的两点 , 如果满足 , 那么称两点互为“等差点”.(1)、请判断在点中,有哪些点与点互为“等差点”?(2)、已知点在直线上,点在双曲线(为常数,且)上,且两点互为“等差点”.请求出点的坐标(用含的代数式表示);(3)、已知抛物线(为常数且)的顶点为点,与轴交于两点,两点分别在抛物线和直线上,如果两点互为“等差点”,且两点的横坐标是一元二次方程的两根,求的值.20. 八年级一班数学兴趣小组在一次活动中进行了探究试验活动,他们将等腰Rt△ABC(∠BAC=90°,AB=AC)放在平面直角坐标系中进行探究,请你和他们一起活动吧。 (1)、如图1所示:若A(1,0),B(0,3),探究得到C点坐标是( , )(2)、如图2所示:若A(0,2),B(-3,0),探究C点坐标(3)、 如图3所示:若A(2,3),B(0,0),探究C点坐标21. 综合与实践.
(1)、如图1所示:若A(1,0),B(0,3),探究得到C点坐标是( , )(2)、如图2所示:若A(0,2),B(-3,0),探究C点坐标(3)、 如图3所示:若A(2,3),B(0,0),探究C点坐标21. 综合与实践. (1)、积累经验
(1)、积累经验我们在第十二章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图1,在△ABC中, , , 线段DE经过点C,且于点D , 于点E . 求证: , 只要证明 , 即可得到解决;
(2)、类比应用如图2,在平面直角坐标系中,中,∠ACB=90°, , 点A的坐标为点C的坐标为 , 求点B的坐标.
(3)、拓展提升如图3,在平面直角坐标系中, , AC=BC,点A的坐标为 , 点C的坐标为 , 则点B坐标为 .
22. 综合与实践:(1)、问题背景:已知 , , , . 在平面直角坐标系中描出这几个点,并分别找到线段和中点、 , 然后写出它们的坐标,则 ▲ , ▲ .
 (2)、探究发现:
(2)、探究发现:结合上述计算结果,你能发现若线段的两个端点的坐标分别为 , , 则线段的中点坐标为 .
(3)、拓展应用:利用上述规律解决下列问题:已知三点 , , , 第四个点与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.
23. 如图,在平面直角坐标系中, , , 且 .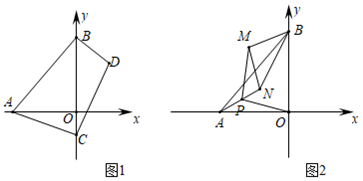 (1)、求 , 的值;(2)、如图 , 为轴负半轴上一点,连 , 过点作 , 使 , 连求证:;(3)、如图 , 若有一等腰 , , 连 , 取中点 , 连、试探究和的关系.24. 阅读材料回答问题
(1)、求 , 的值;(2)、如图 , 为轴负半轴上一点,连 , 过点作 , 使 , 连求证:;(3)、如图 , 若有一等腰 , , 连 , 取中点 , 连、试探究和的关系.24. 阅读材料回答问题在平面直角坐标系中,定义,点P沿着水平和竖直方向运动到达点Q的最短路径的长度为P , Q两点之间的“横纵距离”.如图所示,点A的坐标为 , 则A , O两点的“横纵距离”为5.
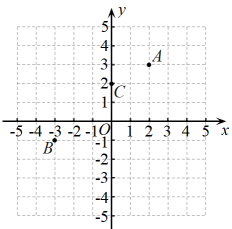
解决问题
(1)、已知点B的坐标为 , 则B , O两点的“横纵距离”为;A , B两点的“横纵距离”为;(2)、已知点C的坐标为 , 写出两个与点C的“横纵距离”为3的点的坐标.(3)、拓展延伸
已知D , O两点的“横纵距离”为5;D , C两点的“横纵距离”为3.请写出满足条件的点D的纵坐标的取值范围.25. 对于点和图形 , 若点关于图形上任意的一点的对称点为点 , 所有点组成的图形为 , 则称图形为点关于图形的“对称图形”在平面直角坐标系中,已知点 , , , .(1)、①在点 , , 中,是点关于线段的“对称图形”上的点有 ▲ .
②画出点关于四边形的“对称图形”;(2)、点是轴上的一动点.若点关于四边形的“对称图形”与关于四边形的“对称图形”有公共点,求的取值范围;
直线与轴交于点 , 与轴交于点 , 线段上存在点 , 使得点是点关于四边形的“对称图形”上的点,直接写出的取值范围.
 26. 在平面直角坐标系中,对于任意三点 , , 的“矩面积”给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积” . 、例如:三点的坐标分别为 , , , 则“水平底” , “铅垂高” , “矩面积” .
26. 在平面直角坐标系中,对于任意三点 , , 的“矩面积”给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积” . 、例如:三点的坐标分别为 , , , 则“水平底” , “铅垂高” , “矩面积” . (1)、若 , , , 则“水平底” ,“铅垂高” , “矩面积”;(2)、若 , , 的“矩面积”为 , 求点的坐标.27. 【阅读理解】
(1)、若 , , , 则“水平底” ,“铅垂高” , “矩面积”;(2)、若 , , 的“矩面积”为 , 求点的坐标.27. 【阅读理解】在平面直角坐标系中,已知点R,S为平面内不重合的两点.给出如下定义:将点R绕点S顺时针旋转90度得到点 , 点关于y轴的对称点为 , 则称点为点R关于点S的“旋对点”.
【迁移应用】
如图,在平面直角坐标系中,直线与x轴相交于点A,与y轴相交于点B.平面内有一点 .
 (1)、请在图中画出点M关于点O的“旋对点” , 并直接写出点M的坐标;(2)、点Q为直线上一动点.
(1)、请在图中画出点M关于点O的“旋对点” , 并直接写出点M的坐标;(2)、点Q为直线上一动点.①若点Q关于点M的“旋对点”为点 , 试探究直线经过某一定点,并求出该定点的坐标;
②在①的条件下,设直线所经过的定点为H,取的中点N,连接 , 求的最小值.
28. 定义:在平面直角坐标系中,已知点 , 且轴,轴,这三个点中任意两个点之间的距离的最小值称为点的“近距”.例如:点的“近距”是3.(1)、已知, .①若A,B,C的“近距”是4,则x的值为;
②点A,B,C的“近距”的最大值为;
(2)、已知点 , 点为线段DE上一动点.当 , , 的“近距”最大时,求此时点P的坐标.29. 阅读材料:在数轴上,点分别表示实数两点之间的距离表示为 , 则 . 若 , 则 , 若 , 则 .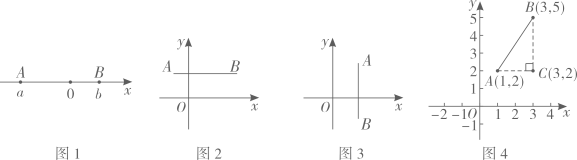
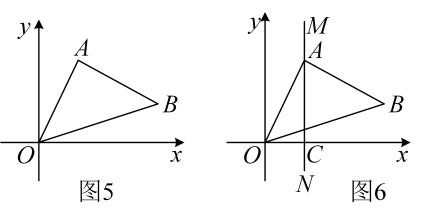
如图1,若点在点的右侧,则 , 类似的,在平面直角坐标系xOy中,点的坐标为 , 点的坐标为 ,
如图2,若轴,则 .
如图3,若轴,则 .
如图4,例如 , 则 .
请根据以上阅读材料,解决下面的问题:
(1)、在平面直角坐标系xOy中,若点A的坐标为(2,4),点B的坐标为(6,4),连接AB,请直接写出线段AB的长度及直线AB与x轴的位置关系;(2)、如图5,△AOB中,若A,B两点的坐标分别为(2,4),(6,2),求△AOB的面积;(3)、如图6,在(2)的条件下,若直线MN经过点C(2,0)且垂直x轴,那么在直线MN上是否存在点P(除A点外),使得△OBP的面积等于△AOB的面积,若存在,请求出P点坐标、若不存在,请说明理由。四、实践探究题
-
30. 五子棋的比赛规则是:只要同色5子连成一条直线为胜利.如图是两人玩的一盘棋,若白棋①的位置是(1,﹣5),黑棋②的位置是(2,﹣4).解答下列问题:
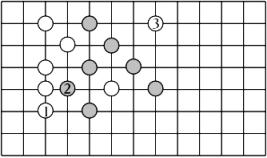 (1)、白棋③的位置是 ;(2)、如果现在轮到黑棋走,黑棋放在 位置就获得胜利了;(3)、如果现在轮到白棋走,白棋放在 位置就获得胜利了.(4)、在(2)的条件下,黑棋获胜了.
(1)、白棋③的位置是 ;(2)、如果现在轮到黑棋走,黑棋放在 位置就获得胜利了;(3)、如果现在轮到白棋走,白棋放在 位置就获得胜利了.(4)、在(2)的条件下,黑棋获胜了.①设此时黑色5子连成直线的表达式是y=ax+b,则方程ax+b=0的解是 .
②若黑色5子连成直线的表达式中y<0,则x的取值范围是 .
31. 将一些相同规格的长方形纸按图①所示方法粘合起来,粘合部分的宽相等.某学校数学综合与实践小组从函数角度进行了如下探究: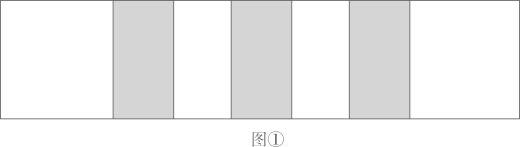
[观察测量]数学综合与实践小组通过观察测量,得到如表:
长方形纸x(张)
1
2
3
4
5
总长度y(厘米)
15
25
35
45
55
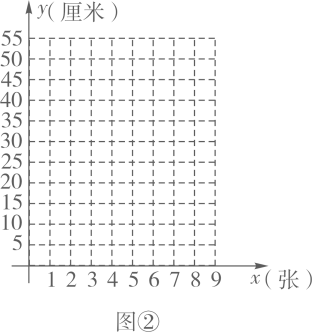 (1)、[探究发现]①建立平面直角坐标系,如图②,横轴表示长方形纸张数石纵轴表示粘合后的总长度y,描出以表格中数据为坐标的各点
(1)、[探究发现]①建立平面直角坐标系,如图②,横轴表示长方形纸张数石纵轴表示粘合后的总长度y,描出以表格中数据为坐标的各点②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如过不在同一条直线上,说明理由.
(2)、[结论应用]应用上述发现的规律让算①当x=20时,粘合后的纸条总长度y为厘米.
②粘合后内纸条总长度y为505厘米时,需使用长方形纸张.
32. 阅读理解半角模型:半角模型是指有公共顶点,锐角等于较大角的一半,且组成这个较大角两边相等,通过翻折或旋转,将角的倍分关系转化为角的相等关系,并进一步构造全等三角形,使条件弱化,这样可把握问题的本质.

 (1)、【问题背景】
(1)、【问题背景】如图1,在四边形中,分别是上的点, , 试探究图1中线段之间的数量关系.
(2)、【初步探索】小亮同学认为解决此问题可以用如下方法:延长到点 , 使 , 连接 , 先证明 , 再证明 , 则可得到线段之间的数量关系是 .
(3)、【探索延伸】如图2,在四边形中, , 分别是上的点, , 上述结论是否仍然成立,并说明理由.
(4)、【结论运用】如图3,在某次军事演习中,舰艇甲在指挥中心(处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以海里/小时的速度前进,舰艇乙沿北偏东的方向以海里/小时的速度前进,小时后,指挥中心观测到甲、乙两舰艇分别到达处,且两舰艇之间的夹角为 , 则此时两舰艇之间的距离为海里.