备考2024年中考数学探究性训练专题27 锐角三角形
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 以下是某数学兴趣小组开展的课外探究活动,探究目的:测量小河两岸的距离,探究过程:在河两岸选取相对的两点P、A,在小河边取的垂线上的一点C,测得米, , 则小河宽等于( )
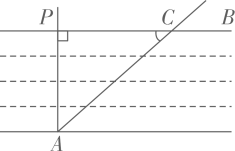 A、米 B、米 C、米 D、米2. 探究;我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.例如在△ABC中,∠A=30°,AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中一个△ABC是直角三角形,如图),则满足已知条件的三角形的第三边AB的长为( )
A、米 B、米 C、米 D、米2. 探究;我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.例如在△ABC中,∠A=30°,AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中一个△ABC是直角三角形,如图),则满足已知条件的三角形的第三边AB的长为( ) A、 B、 C、 或 D、 或3. 东莞市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,操控者和教学楼BC的距离为60米,则教学楼BC的高度是( )米.
A、 B、 C、 或 D、 或3. 东莞市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,操控者和教学楼BC的距离为60米,则教学楼BC的高度是( )米. A、 B、 C、 D、4. 在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )
A、 B、 C、 D、4. 在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )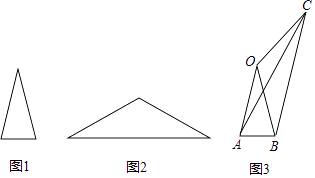 A、∠OCB=2∠ACB B、∠OAB+∠OAC=90° C、AC=2 D、BC=45. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
A、∠OCB=2∠ACB B、∠OAB+∠OAC=90° C、AC=2 D、BC=45. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )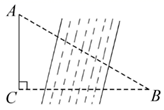 A、 B、 C、 D、6. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正 边形,使用刘徽割圆术,得到π的近似值为( )
A、 B、 C、 D、6. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正 边形,使用刘徽割圆术,得到π的近似值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠,分别在BC、AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG= ,A′G=6,C′G=1,则矩形纸片ABCD的周长为 .
 8. 如图,在 中, , , ,点D是边 上的动点,过点D作 于E点.请探究下列问题:
8. 如图,在 中, , , ,点D是边 上的动点,过点D作 于E点.请探究下列问题: (1)、若 ,则 ;(2)、若 ,设点F是边 上的动点,连接 、 ,以 、 为邻边作平行四边形 ,且使得顶点G恰好落在 边上,则 .9. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.
(1)、若 ,则 ;(2)、若 ,设点F是边 上的动点,连接 、 ,以 、 为邻边作平行四边形 ,且使得顶点G恰好落在 边上,则 .9. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.小组成员查阅相关资料,得到如下信息:
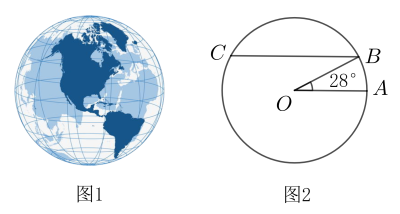
信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图2,赤道半径约为6400千米,弦 , 以为直径的圆的周长就是北纬28°纬线的长度;(参考数据: , , , )
根据以上信息,北纬28°纬线的长度约为千米.
 10. 数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是.
10. 数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是.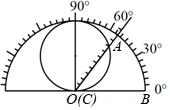
三、理论探究题
-
11. 阅读下列材料,并完成相应的任务.
我们所学的锐角三角函数反映了直角三角形中的边角关系:
如图(1)所示.sin α= , cos α= ,
tan α=.
一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得
sin(α+β)=sin αcos β+cos αsin β;sin(α-β)=sin α
cos β-cos αsin β.

例如:sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°
sin 30°=.
任务:
(1)、计算:sin 75°=;(2)、如图(2)所示,在△ABC中,∠B=15°,∠C=45°,AC=2-2,求AB和BC的长.12. 构建几何图形解决代数问题是“数形结合”思想的体现,在计算时,如图1,在中, , 延长使 , 连接 , 得 , 所以 . 类比这种方法, (1)、类比这种方法,求得;(2)、如图2,锐角 , 已知 , 求证: .13. 阅读下列材料:
(1)、类比这种方法,求得;(2)、如图2,锐角 , 已知 , 求证: .13. 阅读下列材料:在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,求证:
证明:如图1,过点C作CD⊥AB于点D,则:
在Rt△BCD中,CD=asinB,
在Rt△ACD中,CD=bsinA,
∴asinB=bsinA,
根据上面的材料解决下列问题:
(1)、如图2,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,求证:(2)、如图3,现有一片三角形区域需美化,已知∠A=67°,∠B=53°,AC=80m,求这片区域的面积(结果保留根号,参考数据:sin53°≈0.8,sin67°≈0.9).14. 如图1,为等边三角形,其边长为3.点 , 分别在边 , 上,且 , 连接 , 显然有. (1)、问题发现
(1)、问题发现如图2,若将绕点A逆时针旋转一个角度 , 结论“”仍成立吗?请作出判断,并证明你的结论;
(2)、问题解决如图3,在(1)的情形下,当点B , D , E三点正好在一条直线上时,求的长.
15. 综合与实践 (1)、【问题情境】在数学活动课上,同学们以“折叠矩形”为主题开展数学活动.已知,在矩形中, , 点是边上一点,将沿直线折叠,点的对应点为点 .
(1)、【问题情境】在数学活动课上,同学们以“折叠矩形”为主题开展数学活动.已知,在矩形中, , 点是边上一点,将沿直线折叠,点的对应点为点 .
【操作发现】操作一:如图①,当点与点重合时,过点作 , 交于点 , 连结 , 试判定四边形的形状,并说明理由;
操作二:如图②,当点落在边上时,;
(2)、操作三:如图③,当点为中点时,延长交于点 , 连结 , 则 .16. 在中, , , 是边上一点,将沿折叠得到 , 连接 .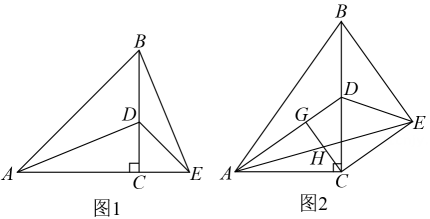 (1)、特例发现
(1)、特例发现
如图 , 当 , 落在直线上时.
求证:;
填空:的值为 ;(2)、类比探究
如图 , 当 , 与边相交时,在上取一点 , 使 , 交于点探究的值用含的式子表示 , 并写出探究过程;(3)、拓展运用
在的条件下,当 , 是的中点时,若 , 求的长.17. 综合与实践:在学习《解直角三角形》一章时,小邕同学对一个角的倍角的三角函数值与这个角的三角函数值是否有关系产生了浓厚的兴趣,并进行研究.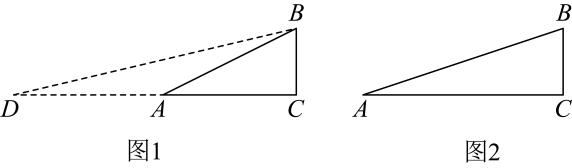 (1)、【初步尝试】我们知道: , .
(1)、【初步尝试】我们知道: , .发现:(填“”或“”).
(2)、【实践探究】在解决“如图1,在中, , , , 求的值”这一问题时,小邕想构造包含的直角三角形,延长到点D,使 , 连接BD,所以可得 , 问题即转化为求的正切值,请按小邕的思路求的值.(3)、【拓展延伸】如图2,在中, , , .请模仿小邕的思路或者用你的新思路,试着求一求的值.18.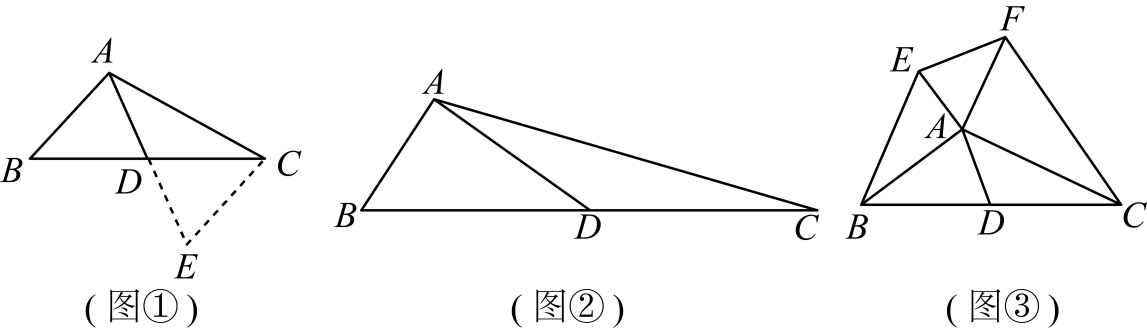 (1)、【问题探究】在学习三角形中线时,我们遇到过这样的问题:如图 , 在中,点为边上的中点, , , 求线段长的取值范围.我们采用的方法是延长线段到点 , 使得 , 连结 , 可证≌ , 可得 , 根据三角形三边关系可求的范围,我们将这样的方法称为“三角形倍长中线”则的范围是: .
(1)、【问题探究】在学习三角形中线时,我们遇到过这样的问题:如图 , 在中,点为边上的中点, , , 求线段长的取值范围.我们采用的方法是延长线段到点 , 使得 , 连结 , 可证≌ , 可得 , 根据三角形三边关系可求的范围,我们将这样的方法称为“三角形倍长中线”则的范围是: .
(2)、【拓展应用】
①如图 , 在中, , , , , 求的长.
②如图 , 在中,为边的中点,分别以、为直角边向外作直角三角形,且满足 , 连结 , 若 , 则 直接写出19.
 (1)、【操作】如图,在矩形纸片中,点 , 点分别是边 , 边上的动点,连结 , 将矩形纸片分别沿直线 , 折叠,点的对应点为点 , 点的对应点为点若点与点重合,与交于点 , 如图 , 求证: .
(1)、【操作】如图,在矩形纸片中,点 , 点分别是边 , 边上的动点,连结 , 将矩形纸片分别沿直线 , 折叠,点的对应点为点 , 点的对应点为点若点与点重合,与交于点 , 如图 , 求证: .
(2)、【探究】a.如图 , 当点 , 落在对角线上时, , , 则 .
b.如图 , 当点 , 落在对角线上时,与交于点 , 与交于点 , 连结 , 若 , , .20. 和均为等边三角形,分别为和的中点,连接 , , .
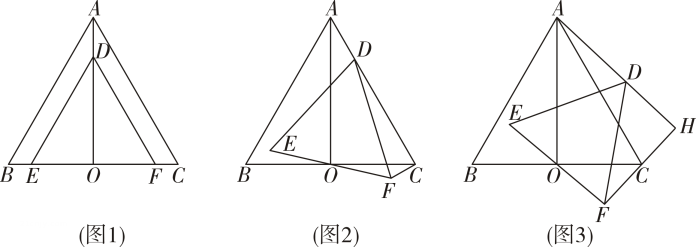 (1)、【特例发现】如图 , 当点 , 点与点分别在 , 上时,可以得出结论: ;直线与直线的位置关系是 .
(1)、【特例发现】如图 , 当点 , 点与点分别在 , 上时,可以得出结论: ;直线与直线的位置关系是 .
(2)、【探究证明】如图 , 将图中的绕点顺时针旋转,使点恰好落在线段上,连接中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)、【拓展运用】如图 , 将图中的绕点顺时针旋转 , 连接 , , 它们的延长线交于点 , 当时:
连接 , 判断四边形的形状,并给予证明;
直接写出的值.21.(1)、【问题呈现】如图1,和都是等边三角形,连接 . 求证: .
 (2)、【类比探究】
(2)、【类比探究】如图2,和都是等腰直角三角形, . 连接 . 请直接写出的值.
(3)、【拓展提升】如图3,和都是直角三角形, , 且 . 连接 . 延长交于点F,交于点G.求的值.
22. 如图

【方法尝试】如图1,矩形是矩形以点A为旋转中心,按逆时针方向旋转所得的图形,分别是它们的对角线.求证:.
【类比迁移】如图2,在和中, , , , , .将绕点在平面内逆时针旋转,设旋转角为 , 连接 , .
①请判断线段和的数量关系和位置关系,并说明理由;
②当点B,D,E在同一直线上时,求线段的长.
【拓展延伸】如图3,在中, , , 过点作 , 在射线上取一点 , 连接 , 使得 , 请直接写出线段的最值.
23.(1)、【探究发现】如图,在正方形中,E为边上一点,将沿BE翻折得到 , 延长交边于点G.求证:; (2)、【类比迁移】如图,在矩形中,E为边上一点,且 , 将沿翻折得到 , 延长交边于点G,延长交边于点H,且 , 求的长;
(2)、【类比迁移】如图,在矩形中,E为边上一点,且 , 将沿翻折得到 , 延长交边于点G,延长交边于点H,且 , 求的长; (3)、【实践创新】如图,为等腰三角形, , O为斜边的中点, M,N为线段上的动点,且满足 , 设 , , , 证明:.
(3)、【实践创新】如图,为等腰三角形, , O为斜边的中点, M,N为线段上的动点,且满足 , 设 , , , 证明:.
四、实践探究题
-
24. 仁皇阁是一个著名景点,某校九年级研学期间参观了仁皇阁,数学兴趣小组对仁皇阁高度产生了浓厚的兴趣,他们想运用所学知识估算出仁皇阁的高度。
课题 估算仁皇阁高度 
测量工具 测量角度的仪器,皮尺,刻度尺等 组别 测量方案示意图 测量方案说明 组1 
如图1 , 先在仁皇阁底部广场的C处用仪器测得阁楼顶端A的仰角为27° , 然后从C处向阁楼底部前进10m到达D处,此时在D处测得阁楼顶端A的仰角为30° . 组2 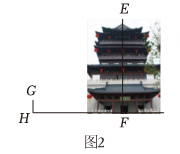
如图2 , 身高1.5m的组员站在仁皇阁正门边上合影.打印出照片后量得此组员图上高度GH为0.5cm,量得仁皇阁图上高度EF为12.9cm. (1)、任务一 请分别计算两组中测量得到的阁楼高度;(结果保留小数点后一位.参考数据)(2)、任务二 后续经过查证后发现小组2数据更为精确,请你帮小组1分析可能产生误差的原因.(写出一条即可)25. 如图1,某人的一器官后面A处长了一个新生物,现需检测其到皮肤的距离.为避免伤害器官,可利用一种新型检测技术,检测射线可避开器官从侧面测量.某医疗小组制定方案,通过医疗仪器的测量获得相关数据,并利用数据计算出新生物到皮肤的距离方案如下:课题 检查新生物到皮肤的距离 工具 医疗仪器等 示意图 
说明 如图2,新生物在A处,先在皮肤上选择最大限度地避开器官的B处照射新生物,检测射线与皮肤MN的夹角为∠DBN;再在皮肤上选择距离B处9 cm的C处照射新生物,检测射线与皮肤MN的夹角为∠ECN.
测量数据 ∠DBN=35°,∠ECN=22°,BC=9cm. 请你根据上表中的测量数据,计算新生物A处到皮肤的距离(结果精确到0.1cm,参考数据:sin35°≈0.57,cos35°≈0.82,tan35≈0.70,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40).
26. 【问题背景】
在一次数学实践活动中,张老师将班级学生分成“扶摇”、“惊鸿”、“骐骥”三个小组,运用直角三角尺测量三个不同直尺的宽度直尺的每两个长刻度之间的长度是
【实践探究】
(1)、扶摇组同学用含的三角尺,提出按照图的方案,直尺与直角三角尺的边重合,另一边分别交 , 于点 , 点 , , , 的读数分别为 , , , , 则该直尺的宽度的长为 ;
(2)、惊鸿组同学用含的三角尺,提出按照图的方案,直尺与直角三角尺的斜边重合,另一边分别交 , 于点 , 点 , , , 的读数分别为 , , , , 求该直尺的宽度;
(3)、骐骥组同学用含的三角尺,提出按照图的方案,直尺与直角三角尺斜平行,直分别交 , 于点 , , , 点 , , , 的读数分别为 , , , , , 直接写出该直尺的宽度结果精确到参考数据:27. 综合与实践:【问题情境】:通过查看出厂包装袋上的数据,数学活动小组的同学发现纸的长与宽分别为和 , 其比值为 , 而 , 他们上网查阅资料也发现纸的长与宽的比是一个特殊值“”不妨定义长与宽的比为的矩形为“标准矩形”【操作实践】:如图 , 数学活动小组的同学在几何画板软件上画了一个正方形 , 连接对角线 , 在射线上截取了 , 过点作交的延长线于点 , 令 .
【问题探究】:
(1)、求证:四边形为“标准矩形”;(2)、如图 , 数学活动小组的同学在图的基础上隐藏了线段 , 在线段上取一点 , 连接 , .当平分时,求的长;
当的周长最小时,求的正切值.
28. 某“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测最仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整).课题
测量旗杆的高度

成员
组长××× 组员:×××,×××,×××
测量工具
测量角度的仪器、皮尺等
测量示意图

说明:线段表示学校旗杆,测量角度的仪器的高度 , 测点A,B与H在同一条水平直线上,A,B之间的距离可以直接测得,且点G,H,A,B,C,D都在同一竖直平面内.点C,D,E在同一条直线上,点E在上.
测量项目
第一次
第二次
平均值
测量数据
的度数
的度数
A,B之间的距离
任务一:两次测量,A,B之间的距离的平均值是 ▲ m.
任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆的高度.
(参考数据: , , , , , )
任务三:该“综合与实践”小组在制订方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳,你认为其原因可能是什么?
29. 问题:如何设计“倍力桥”的结构?图1是搭成的“倍力桥”,纵梁a,c夹住横梁 , 使得横梁不能移动,结构稳固.图2是长为 , 宽为3cm的横梁侧面示意图,三个凹槽都是半径为1cm的半圆,圆心分别为 , 纵梁是底面半径为1cm的圆柱体,用相同规格的横梁、纵梁搭“桥”,间隙忽略不计.
探究1:

(1)、图3是“桥”侧面示意图,A,B为横梁与地面的交点,C,E为圆心,是横梁侧面两边的交点,测得 , 点到AB的距离为12cm,试判断四边形的形状,并求的值.(2)、若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.①若有12根横梁绕成环,图4是其侧面示意图,内部形成十二边形 , 求的值;
②若有根横梁绕成的环(为偶数,且 , 试用关于的代数式表示内部形成的多边形的周长.
30. 我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”,数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透在我校的数学选修课上,同学们针对四边形面积求解的问题进行了探究: (1)、【问题提出】
(1)、【问题提出】如图 , 在▱中, , , , 是的中点,点在上,且 , 求四边形的面积;结果保留根号
(2)、【问题解决】如图所示,现规划在一处滩地上规划一个五边形河畔公园 , 按设计要求,要在五边形河畔公园内挖一个四边形人工湖 , 使点、、、分别在边、、、上,且满足 , 已知五边形中, , , , , , 为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小请问,是否存在符合设计要求的面积最小的四边形人工湖?若存在,求四边形面积的最小值及这时点到点的距离;若不存在,请说明理由.