备考2024年中考数学探究性训练专题25 图形的相似
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为 , 当测试距离为时,最大的“”字高度为( )
 A、 B、 C、 D、2. 如图,正方形边长为4,点E在边上运动,在的左侧作等腰直角三角形 , , 连接.喜欢探究的小亮通过独立思考,得到以下两个结论:①当点E与点D重合时,;②当线段最短时,.下列判断正确的是( )
A、 B、 C、 D、2. 如图,正方形边长为4,点E在边上运动,在的左侧作等腰直角三角形 , , 连接.喜欢探究的小亮通过独立思考,得到以下两个结论:①当点E与点D重合时,;②当线段最短时,.下列判断正确的是( ) A、①,②都正确 B、①,②都错误 C、①正确,②错误 D、①错误,②正确3. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段MN分为两线段MG、GN,使得其中较长的一段MG是全长MN与较短的一段GN的比例中项,即满足 ,后人把 这个数称为“黄金分割数”,把点G称为线段MN的“黄金分割点”.如图,在△ABC中,已知AB=AC=3,BC=4,若点D是边BC边上的一个“黄金分割点”,则△ADC的面积为( )
A、①,②都正确 B、①,②都错误 C、①正确,②错误 D、①错误,②正确3. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段MN分为两线段MG、GN,使得其中较长的一段MG是全长MN与较短的一段GN的比例中项,即满足 ,后人把 这个数称为“黄金分割数”,把点G称为线段MN的“黄金分割点”.如图,在△ABC中,已知AB=AC=3,BC=4,若点D是边BC边上的一个“黄金分割点”,则△ADC的面积为( )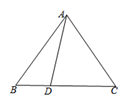 A、 B、 C、 D、4. 在研究相似问题时,甲、乙同学的观点如下:
A、 B、 C、 D、4. 在研究相似问题时,甲、乙同学的观点如下: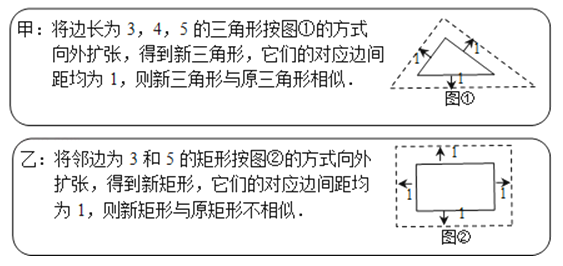
对于两人的观点,下列说法正确的是( )
A、两人都对 B、两人都不对 C、甲对,乙不对 D、甲不对,乙对5. 如图,将的圆周分成五等分(分点为A、B、C、D、E),依次隔一个分点相连,即成一个正五角星形.小张在制图过程中,惊讶于图形的奇妙,于是对图形展开了研究,得到:点M是线段AD、BE的黄金分割点,也是线段NE、AH的黄金分割点.在以下结论中,不正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 四边形ABCD是一张矩形纸片,点E在AD上,将△ABE沿BE折叠,使点A落在矩形的对角线BD上,连接CF,若DE=1,请探究下列问题:
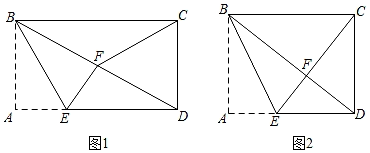 (1)、如图1,当F恰好为BD的中点时,AE=;(2)、如图2,当点C、E、F在同一条直线上时,AE= .7. 为了测量校园水平地面上一棵不可攀爬的树的高度,小明利用物理学中“光的反射定律”做了如下的探索:如图,找一面很小的镜子放在合适的位置(点E处),小明站在点D处刚好能在镜子里看到树梢顶点,此时小明看镜子的视线与地面的夹角为(即),镜子到大树的水平距离为30米,则树的高度为米(注:反射角等于入射角,结果若有根号则保留根号).
(1)、如图1,当F恰好为BD的中点时,AE=;(2)、如图2,当点C、E、F在同一条直线上时,AE= .7. 为了测量校园水平地面上一棵不可攀爬的树的高度,小明利用物理学中“光的反射定律”做了如下的探索:如图,找一面很小的镜子放在合适的位置(点E处),小明站在点D处刚好能在镜子里看到树梢顶点,此时小明看镜子的视线与地面的夹角为(即),镜子到大树的水平距离为30米,则树的高度为米(注:反射角等于入射角,结果若有根号则保留根号). 8. 如图1,在Rt△ABC中,∠C=90°,AC=3,BC=4,求作菱形DEFG,使点D在边AC上,点E、F在边AB上,点G在边BC上.小明发现所作的四边形DEFG是菱形,于是小明进一步探索,发现可作出的菱形的个数随着点D的位置变化而变化,当菱形的个数只有1个时CD的长的取值范围为.
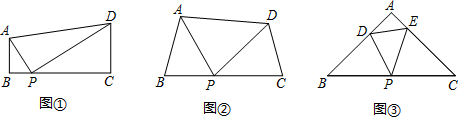
8. 如图1,在Rt△ABC中,∠C=90°,AC=3,BC=4,求作菱形DEFG,使点D在边AC上,点E、F在边AB上,点G在边BC上.小明发现所作的四边形DEFG是菱形,于是小明进一步探索,发现可作出的菱形的个数随着点D的位置变化而变化,当菱形的个数只有1个时CD的长的取值范围为. 9. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
9. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,则DE的长为.
 10. 如图1是2002年发行的中国纪念邮票,其图案是三国时期吴国数学家赵爽在注释《周髀算经》中所给勾股定理的证明.同学们在探索勾股定理时还出现了许多利用正方形证明勾股定理的方法.如图2,正方形ABCD是由四个全等的直角三角形和一个正方形EFGH拼成;正方形EFGH是由与上述四个直角三角形全等的三角形和正方形IJKL拼成;正方形ABCD,EFGH,IJKL的面积分别为S1 , S1 , S3分别连结AK,BL,CI,DJ并延长构成四边形MNOP,它的面积为m.①请用等式表示S1 , S1 , S3之间的数量关系为:;②m=(用含S1 , S3的代数式表示m)
10. 如图1是2002年发行的中国纪念邮票,其图案是三国时期吴国数学家赵爽在注释《周髀算经》中所给勾股定理的证明.同学们在探索勾股定理时还出现了许多利用正方形证明勾股定理的方法.如图2,正方形ABCD是由四个全等的直角三角形和一个正方形EFGH拼成;正方形EFGH是由与上述四个直角三角形全等的三角形和正方形IJKL拼成;正方形ABCD,EFGH,IJKL的面积分别为S1 , S1 , S3分别连结AK,BL,CI,DJ并延长构成四边形MNOP,它的面积为m.①请用等式表示S1 , S1 , S3之间的数量关系为:;②m=(用含S1 , S3的代数式表示m)
三、理论探究题
-
11. 阅读下面材料:小腾遇到这样一个问题:如图 , 在中,点在线段上, , , , , 求的长.

小腾发现,过点作 , 交的延长线于点 , 通过构造 , 经过推理和计算能够使问题得到解决如图 .
请回答:(1)、的度数为 , 的长为 .
(2)、参考小腾思考问题的方法,解决问题:
如图 , 在四边形中, , , , 与交于点 , , , 求的长.12. 【教材呈现】华师版九年级上册63页例1.
如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5,求BC的长.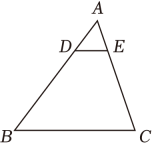
【应用拓展】
(1)、如图①,在△ABC中,点D是边AB的中点,点F为BC延长线上一点,连接DF交AC于点E,若DE:EF=3:1,DG∥AC,EC=2,则AC的长为 . (2)、如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连接DE交AC于点F,若点A为DB的中点,CE:EB=1:2,△DBE的面积为4,则△CFE(阴影部分)面积为 .
(2)、如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连接DE交AC于点F,若点A为DB的中点,CE:EB=1:2,△DBE的面积为4,则△CFE(阴影部分)面积为 . 13. 两千多年前,古希腊数学家欧多克索斯发现:将一条线段AB分割成长、短两条线段AP、PB,若 , 则把这种分割叫做黄金分割,点P叫做线段AB的黄金分割点,这个比值叫做黄金比.
13. 两千多年前,古希腊数学家欧多克索斯发现:将一条线段AB分割成长、短两条线段AP、PB,若 , 则把这种分割叫做黄金分割,点P叫做线段AB的黄金分割点,这个比值叫做黄金比.图①
 图②
图②  图③
图③ (1)、如图①,点P是线段AB的黄金分割点,设 , , 求黄金比x的值.
(1)、如图①,点P是线段AB的黄金分割点,设 , , 求黄金比x的值.(精确到0.001,参考数据: , , , )
(2)、如图②,在△ABC中, , , BD是△ABC的角平分线.求证:点D是线段AC的黄金分割点.
(3)、如图③,点E是正方形ABCD的BC边的中点,以点E为圆心以ED长为半径画弧,交射线BC于点F,过点F作交射线AD于点G.若 , 请直接写出AB的长.14. 定义:如果两条线段将一个三角形分成3个等腰三角形,那么我们把这两条线段叫做这个三角形的三分线.(1)、请你在图1中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种).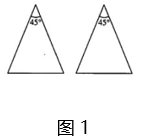 (2)、在△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.(3)、如图2,在△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长.
(2)、在△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.(3)、如图2,在△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长.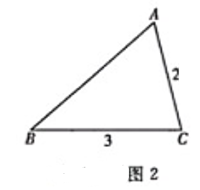 15.(1)、数学活动课上,老师出示了一个问题;如图1,在矩形ABCD中,E是边AB上一点,DF⊥CE于点F,GD⊥DF,AG⊥DG,AG=CF,试猜想四边形ABCD的形状,并说明理由.
15.(1)、数学活动课上,老师出示了一个问题;如图1,在矩形ABCD中,E是边AB上一点,DF⊥CE于点F,GD⊥DF,AG⊥DG,AG=CF,试猜想四边形ABCD的形状,并说明理由. (2)、【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形ABCD中,E是边AB上一点,DF⊥CE于点F,AH⊥CE于点H,GD⊥DF交HA的延长线于点G,可以用等式表示线段FH,AH,CF的数量关系,请你思考并解答这个问题:
(2)、【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形ABCD中,E是边AB上一点,DF⊥CE于点F,AH⊥CE于点H,GD⊥DF交HA的延长线于点G,可以用等式表示线段FH,AH,CF的数量关系,请你思考并解答这个问题: (3)、【拓展迁移】小博深入研究小睿提出的这个问.题,发现并提出了新的探究点:如图3,在正方形ABCD中,E是边AB上一点,AH⊥CE交CE的延长线于点H,点M在CH上,且AH=HM,连结AM,BH,可以用等式表示线段CM,BH的数量关系,请你思考并解答这个问题.
(3)、【拓展迁移】小博深入研究小睿提出的这个问.题,发现并提出了新的探究点:如图3,在正方形ABCD中,E是边AB上一点,AH⊥CE交CE的延长线于点H,点M在CH上,且AH=HM,连结AM,BH,可以用等式表示线段CM,BH的数量关系,请你思考并解答这个问题. 16. 【教材呈现】下面是华师版教材九年级上册52页的部分内容:
16. 【教材呈现】下面是华师版教材九年级上册52页的部分内容:我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系: . 这就是如下的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.(简称“平行线分线段成比例”)

 (1)、【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过E作EF∥AD交边DC于点F,点P、Q分别在矩形的边AD、BC上,连结PQ交EF于点M.求证:PM=QM.(2)、【结论应用】如图②,在【问题原型】的基础上,点R在边BC上(不与点Q重合),连结PR交EF于点N.
(1)、【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过E作EF∥AD交边DC于点F,点P、Q分别在矩形的边AD、BC上,连结PQ交EF于点M.求证:PM=QM.(2)、【结论应用】如图②,在【问题原型】的基础上,点R在边BC上(不与点Q重合),连结PR交EF于点N.
若MN=4,则线段QR的长为 ;(3)、当点Q与点B重合,点R与点C重合时,如图③,若BC=10,且△PMN周长的最小值为12,则边AB的长为 .17. 如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE . (1)、探索发现:
(1)、探索发现:图1中,的值为 , 的值为 .
(2)、拓展探究若将△CDE绕点C旋转,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.
(3)、问题解决当△CDE旋转至A , D , C三点共线时,直接写出线段BE的长.
18. (1)、问题发现
(1)、问题发现如图1,在中, , D是线段上一动点,以为一条边在A的左侧作 , 使 , 连接 . 则与的数量关系为 .
(2)、类比探究如图2,在中,D是线段上一动点,以为一条边在的左侧作 , 使且 , 连接 . 则(1)中与的数量关系仍然成立吗?请说明理由.
(3)、拓展应用如图3,在(2)的条件下,若 , , 当取最小值时,的面积为 .
19. 定义:长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.操作1:将正方形沿过点的直线折叠,使折叠后的点落在对角线上的点处,折痕为 .
操作2:将沿过点的直线折叠,使点 , 点分别落在边 , 上,折痕为 .
则四边形为矩形.
证明:设正方形的边长为1,则 .
由折叠性质可知 , , 则四边形为矩形,
∴ , ∴ .
∴ , 即 , ∴ , ∴ ,
∴四边形为矩形.

阅读以上内容,回答下列问题:
(1)、在图①中,所有与相等的线段是、 , 的值是;(2)、已知四边形为矩形,模仿上述操作,得到四边形 , 如图②,求证:四边形为矩形;(3)、将图②中的矩形沿用(2)中的方式操作3次后,得到一个“矩形”,则的值是 .20. 已知四边形ABCD中,E , F分别是AB , AD边上的点,DE与CF交于点G , 令=k .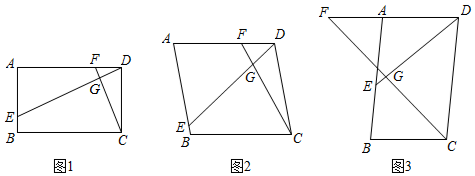 (1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.21. 如图
(1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.21. 如图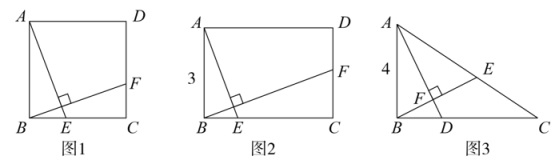 (1)、综合与探究,如图1,在正方形中,点E , F分别在边上,且 , 则线段与的之间的数量关系为;(2)、【类比探究】如图2,在矩形中, , , 点E , F分别在边上,且 , 请写出线段与的数量关系,并证明你的结论.(3)、【拓展延伸】如图3,在中, , , , D为上一点,且 , 连接 , 过点B作于点F , 交于点E , 求的长.22. 如图
(1)、综合与探究,如图1,在正方形中,点E , F分别在边上,且 , 则线段与的之间的数量关系为;(2)、【类比探究】如图2,在矩形中, , , 点E , F分别在边上,且 , 请写出线段与的数量关系,并证明你的结论.(3)、【拓展延伸】如图3,在中, , , , D为上一点,且 , 连接 , 过点B作于点F , 交于点E , 求的长.22. 如图
【问题原型】华师版教材八年级下册第121页有这样一道题:
如图1,在正方形ABCD中,CE⊥DF.求证:CE=DF.
请你完成这一问题的证明过程.
【问题应用】如图,在正方形ABCD中,AB=4,E、F分别是边AB、BC上的点,且AE=BF.
(1)、如图2,连接CE、DF交于点G,H为GE的中点,连接DH,FH.当E为AB的中点时,四边形CDHF的面积为 ;(2)、如图3,连接DE、DF,当点E在边AB上运动时,DE+DF的最小值为 .23. 综合与实践如图,在中, , 点P以每秒2个单位长度的速度从点A出发,沿方向向终点B匀速运动,同时点Q以每秒1个单位长度的速度从点C出发,沿方向向终点A匀速运动,连接 . 设运动的时间为t秒.
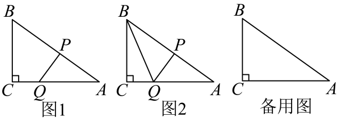 (1)、求的长(用含t的代数式表示).(2)、当秒时,求的面积.(3)、如图2,连接 , 当为直角三角形时,求所有满足条件t的值.24. 阅读下列材料,解决问题:
(1)、求的长(用含t的代数式表示).(2)、当秒时,求的面积.(3)、如图2,连接 , 当为直角三角形时,求所有满足条件t的值.24. 阅读下列材料,解决问题:配方法是数学中一种很重要的恒等变形方法,我们已经学习了用配方法解一元二次方程,并在此基础上得出了一元二次方程的求根公式.其实配方法还有很多重要的应用.例如我们可以用配方法求代数式的最值及取得最值的条件,如下面的例子:
例:求多项式的最小值
解:
,
多项式的最小值为−7,此时, .
仿照上面的方法,解决下面的问题:
(1)、当时,多项式有最值是;(2)、若代数式 , 试比较与的大小关系;(3)、如图,在中, , 高 , 矩形的四个顶点分别在三角形的三边上,设 , 矩形的面积为 . 用含有的代数式表示 , 并求出当的值为多少时,的值最大?并判断此时与面积的关系. 25.
25. (1)、【观察与猜想】
(1)、【观察与猜想】如图1,点是矩形内一点,过点的直线 , 分别交矩形的边为点 . 若 , 则;
(2)、【类比探究】如图2,在平行四边形中,点分别在边上,连接与交于点 . 求证:;
(3)、【拓展延伸】如图3,在四边形中, , 在边上,连接与交于点 , 当时,求的值.
26. 如图①,在正方形ABCD中,点E , F分别在边AB、BC上,DF⊥CE于点O , 点G , H分别在边AD、BC上,GH⊥CE . (1)、问题解决:①写出DF与CE的数量关系:;
(1)、问题解决:①写出DF与CE的数量关系:;②的值为 ;
(2)、类比探究,如图②,在矩形ABCD中,(k为常数),将矩形ABCD沿GH折叠,使点C落在AB边上的点E处,得到四边形EFGH交AD于点P , 连接CE交GH于点O . 试探究GH与CE之间的数量关系,并说明理由;(3)、拓展应用,如图③,四边形ABCD中,∠BAD=90°,AB=BC=6,AD=CD=4,BF⊥CE , 点E、F分别在边AB、AD上,求的值.四、实践探究题
-
27. 【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2.小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F , 落在墙上的点E处,点E到地面的高度 , 点F到地面的高度 , 灯泡到木板的水平距离 , 木板到墙的水平距离为.图中点A , B , C , D在同一条直线上.

图1 图2
(1)、求BC的长;(2)、求灯泡到地面的高度AG.28. 根据以下素材,探索解决问题.测量旗杆的高度

素材1 可以利用影子测量旗杆的高度.如图1,光线 , DN,BM分别是旗杆和小陈同学在同一时刻的影子.
素材2 可以利用镜子测量旗杆的高度.如图2,小陈同学从镜子E中刚好可以看见旗杆的顶端C,测得.
素材3 可以利用标杆测量旗杆的高度.如图3,点G,P,C在同一直线上,标杆 , 测得 , . (说明:小陈同学、旗杆CD与标杆PQ均垂直于地面,小陈同学的眼睛G离地面的距离)
(1)、任务1 利用素材1证明△ABM△CDN;(2)、任务2 在素材2中,小陈同学还要测量图中哪条线段的长度(旗杆无法直接测量),才能求出旗杆的高度?若把该线段的长度记为a,请你用含a的式子表示出旗杆的高度;(3)、任务3 利用素材3求出旗杆的高度.29. 在学习了光的反射定律后,数学综合实践小组想利用光的反射定律(反射角等于入射角)测量池塘对岸一棵树的高度AB , 测量步骤如下:
①如图,在地面上的点E处放置一块平面镜(镜子大小忽略不计),小阳站在BE的延长线上,当小阳从平面镜中刚好看到树的顶点A时,测得小阳到平面镜的距离DE=2m , 小阳的眼睛点C到地面的距离CD=1.6m;
②将平面镜从点E沿BE的延长线移动6m放置到点H处,小阳从点D处移动到点G , 此时小阳的眼睛点F又刚好在平面镜中看到树的顶点A , 这时测得小阳到平面镜的距离GH=3.2m . 请根据以上测量过程及数据求出树的高度AB .
30. 通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影. (1)、【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
(1)、【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
(2)、【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为____ ;
A、
B、
B、
C、
C、
D、
D、
(3)、【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.31. 某校项目式学习小组开展项目活动,过程如下:
(3)、【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.31. 某校项目式学习小组开展项目活动,过程如下:项目主题:测量旗杆高度

问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如自制的直角三角形硬纸板,标杆,镜子,甚至还可以利用无人机…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
方案一
方案二
…
测量工具
标杆,皮尺
自制直角三角板硬纸板,皮尺
…
测量示意图

说明:线段AB表示学校旗杆,小明的眼睛到地面的距离CD=1.7m,测点F与B,D在同一水平直线上,D,F,B之间的距离都可以直接测得,且A,B,C,D,E,F都在同一竖直平面内,点A,C,E三点在同一直线上.

说明:线段AB表示旗杆,小明的身高CD=1.7m,测点D与B在同一水平直线上,D,B之间的距离可以直接测得,且A,B,C,D,E,F,G都在同一竖直平面内,点A,C,E三点在同一直线上,点C,F,G三点在同一直线上.
测量数据
B,D之间的距离
16.8m
B,D之间的距离
16.8m
…
D,F之间的距离
1.35m
EF的长度
0.50m
…
EF的长度
2.60m
CE的长度
0.75m
…
…
…
根据上述方案及数据,请你选择一个方案,求出学校旗杆AB的高度.(结果精确到0.1m);
32. (1)、问题提出 如图①,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE,若AD=9,∠DCE=15°,求△BCE外接圆的半径长.(2)、问题解决 某社区准备设计一个矩形花园,如图②是花园的示意图,图中EF,EG,FG,FC是花园内四条小路,这四条小路将花园分成五个三角形区域,分别用来种植不同种类的花.根据设计要求,∠EGF=∠BCF,∠EFC=90°,DF:DC=1:2,AE=8米.该矩形花园面积是否存在最大值?若存在,请求出其最大面积;若不存在,请说明理由.33.
(1)、问题提出 如图①,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE,若AD=9,∠DCE=15°,求△BCE外接圆的半径长.(2)、问题解决 某社区准备设计一个矩形花园,如图②是花园的示意图,图中EF,EG,FG,FC是花园内四条小路,这四条小路将花园分成五个三角形区域,分别用来种植不同种类的花.根据设计要求,∠EGF=∠BCF,∠EFC=90°,DF:DC=1:2,AE=8米.该矩形花园面积是否存在最大值?若存在,请求出其最大面积;若不存在,请说明理由.33. (1)、【问题背景】
(1)、【问题背景】由光的反射定律知:反射角等于入射角(如图1,即).小军测量某建筑物高度的方法如下:在地面点E处平放一面镜子,经调整自己位置后,在点D处恰好通过镜子看到建筑物AB的顶端A . 经测得,小军的眼睛离地面的距离 , , , 求建筑物AB的高度.
(2)、【活动探究】观察小军的操作后,小明提出了一个测量广告牌高度的做法(如图2):他让小军站在点D处不动,将镜子移动至处,小军恰好通过镜子看到广告牌顶端G , 测出;再将镜子移动至处,恰好通过镜子看到广告牌的底端A , 测出 . 经测得,小军的眼睛离地面距离 , , 求这个广告牌AG的高度.
(3)、【应用拓展】小军和小明讨论后,发现用此方法也可测量出斜坡上信号塔AB的高度,他们给出了如下测量步骤(如图3):①让小军站在斜坡的底端D处不动(小军眼睛离地面距离),小明通过移动镜子(镜子平放在坡面上)位置至E处,让小军恰好能看到塔顶B;②测出;③测出坡长;④测出坡比为(即).通过他们给出的方案,请你算出信号塔AB的高度(结果保留整数).