备考2024年中考数学探究性训练专题22 图形的轴对称
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 雪花、风车….展示着中心对称的美,利用中心对称,可以探索并证明图形的性质,请思考在下列图形中,是中心对称图形但不一定是轴对称图形的为( )A、扇形 B、平行四边形 C、等边三角形 D、矩形2. 如图,在学习了轴对称后,小华在课外研究三角板时发现“两块完全相同的含有30°的三角板可以拼成一个等边三角形”,请你帮他解决以下问题:在直角△ABC中,∠ACB=90°,∠A=30°,AC=6,BC= ,点E,P分别在斜边AB和直角边AC上,则EP+BP的最小值是( )
 A、 B、4 C、6 D、3. 在探究“过直线外一点P作已知直线a的平行线”的活动中,王玲同学通过如下的折纸方式找到了符合要求的直线,在这个过程中她可能用到的推理依据组合是( )
A、 B、4 C、6 D、3. 在探究“过直线外一点P作已知直线a的平行线”的活动中,王玲同学通过如下的折纸方式找到了符合要求的直线,在这个过程中她可能用到的推理依据组合是( )
①平角的定义;②邻补角的定义;③角平分线的定义;④同旁内角互补,两直线平行;⑤两直线平行,内错角相等.
A、②④ B、③⑤ C、①②⑤ D、①③④二、填空题
-
4. “希望小组”的同学们利用课余时间对“纸片中的折叠问题”进行了探究.如图,在中, , , 点D是边上不与端点B,C重合的一个动点,第一步,将沿折叠,点B的对应点为;第二步,将沿折叠,点D的对应点为 , 当直线过的一个顶点时,线段的长度为.
 5. 小南利用几何画板画图,探索结论,他先画∠MAN=90°,在射线AM上取一点B,在射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD、BD,得到如图所示图形,移动点C,小南发现:当AD=BC时,∠ABD=90°;请你继续探索;当2AD=BC时,∠ABD的度数是.
5. 小南利用几何画板画图,探索结论,他先画∠MAN=90°,在射线AM上取一点B,在射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD、BD,得到如图所示图形,移动点C,小南发现:当AD=BC时,∠ABD=90°;请你继续探索;当2AD=BC时,∠ABD的度数是.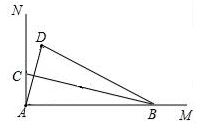
6. 利用图形分.和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是长方形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=6,b=3,则长方形ABCD的面积是 . 7. 如图,某数学兴趣小组在学完矩形的知识后一起探讨了一个纸片折叠问题:如何将一张平行四边形纸片 的四个角向内折起,拼成一个无缝隙、无重叠的矩形 .图中 , , , 表示折痕,折后 的对应点分别是 .若 , , ,则纸片折叠时 的长应取 .
7. 如图,某数学兴趣小组在学完矩形的知识后一起探讨了一个纸片折叠问题:如何将一张平行四边形纸片 的四个角向内折起,拼成一个无缝隙、无重叠的矩形 .图中 , , , 表示折痕,折后 的对应点分别是 .若 , , ,则纸片折叠时 的长应取 . 8. 数学兴趣小组的同学拿出如图所示的矩形纸片 , 其中 , 他们将纸片对折使、重合,展开后得折痕 , 又沿折叠使点C落在处,展开后又得到折痕 , 再沿折叠使点A落在上的处,大家发现了很多有趣的结论.就这个图形,请你探究的值为 .
8. 数学兴趣小组的同学拿出如图所示的矩形纸片 , 其中 , 他们将纸片对折使、重合,展开后得折痕 , 又沿折叠使点C落在处,展开后又得到折痕 , 再沿折叠使点A落在上的处,大家发现了很多有趣的结论.就这个图形,请你探究的值为 . 9. 数学兴趣小组开展以下折纸活动:先对折矩形 (已知 , ),使 和 重合,得到折痕 ,把纸片展平;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 ,延长 交 于点 .同学们通过观察、探究、计算得到下列结论:① ,② 是等边三角形,③ ,④ .其中正确的结论的序号是.
9. 数学兴趣小组开展以下折纸活动:先对折矩形 (已知 , ),使 和 重合,得到折痕 ,把纸片展平;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 ,延长 交 于点 .同学们通过观察、探究、计算得到下列结论:① ,② 是等边三角形,③ ,④ .其中正确的结论的序号是.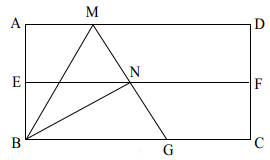 10. 龙岗区八年级某班级在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.
10. 龙岗区八年级某班级在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.

请利用上述模型解决下列问题:
(1)、格点应用:如图2,边长为1的正方形网格内有两点A、B,直线l与A、B的位置如图所示,点P是直线l上一动点,则PA+PB的最小值为;(2)、几何应用:如图3,△ABC中,∠C=90°,AC=4,BC=6,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为;(3)、代数应用:代数式(0≤x≤6)的最小值为;三、实践探究题
-
11. 综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
 (1)、操作判断
(1)、操作判断操作一:对折矩形纸片ABCD , 使AD与BC重合,得到折痕EF , 把纸片展平;
操作二:在AD上选一点P , 连接BP , 沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM , BM .
如图1,当点M在EF上时,根据以上操作,写出一个度数为30°的角为;
(2)、迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q , 连接BQ .
①如图2,当点M在EF上时,则∠MBQ= ▲ ;
②改变点P在AD上的位置(点P不与点A , D重合)如图3,判断∠MBQ 与∠CBQ 的数量关系,并说明理由;
(3)、拓展应用在(2)的探究中,已知正方形纸片ABCD的边长为8cm , 当FQ=1cm 时,请直接写出AP的长.
12. 综合与实践课上,老师让同学们以“正方形的折叠”为主题开展数学活动. (1)、操作判断
(1)、操作判断操作:如图1,点E是边长为12的正方形纸片ABCD的边AD上一动点,将正方形沿着CE折叠,点D落在点F处,把纸片展平,射线DF交射线AB于点P .
判断:根据以上操作,图1中AP与EF的数量关系:;
(2)、迁移探究在(1)条件下,若点E是AD的中点,如图2,延长CF交AB于点Q , 点Q的位置是否确定?如果确定,求出线段BQ的长度;如果不确定,说明理由;
(3)、拓展应用在(1)条件下,如图3,CE , DF交于点G , 取CG的中点H , 连接BH , 则BH的最小值是 .
13. 折叠问题是我们常见的数学问题,它是利用图形变化的轴对称性质解决的相关问题.数学活动课上,同学们以“矩形的折叠”为主题开展了数学活动.【操作】如图1,在矩形中,点M在边上,将矩形纸片沿所在的直线折叠,使点D落在点处,与交于点N.
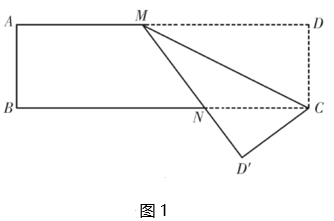
【猜想】
(1)、【验证】请将下列证明过程补充完整:∵矩形纸片沿所在的直线折叠
∴ ▲
∵四边形是矩形
∴(矩形的对边平行)
∴ ▲ ( )
∴ ▲ ▲ (等量代换)
∴( )
(2)、【应用】如图2,继续将矩形纸片折叠,使恰好落在直线上,点A落在点处,点B落在点处,折痕为.

①猜想与的数量关系,并说明理由;
②若 , , 求的长.
14. 综合与实践【问题情境】
在数学活动课上,同学们以“折叠矩形”为主题开展数学活动.已知,在矩形中, , , 点P是边上一点,将沿直线折叠,点A的对应点为点 .

【操作发现】
(1)、操作一:如图①,当点P与点B重合时,过点作 , 交于点 , 连接 , 试判定四边形的形状,并说明理由;(2)、操作二:如图②,当点落在边上时, ▲ ;(3)、操作三:如图③,当点为中点时,延长交于点 , 连接 , 则 ▲ .15. 课本呈现:直觉的误差
有一张的正方形纸片,面积是把这张纸片按图所示剪开成四小块,其中两块是三角形,另外两块是四边形,把剪出的个小块按图所示重新拼合,这样就得到了一个的长方形,面积是 , 面积多了 , 这是为什么?
小明给出如下证明:如图 , 可知, , ,
,
.
,
,
.
因此、、三点不共线同理、、三点不共线,所以拼合的长方形内部有空隙,故面积多了 .
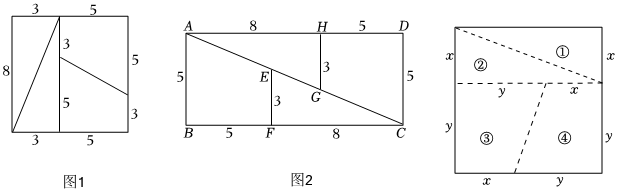
问题探究:(1)、小红给出的证明思路为:以为原点,所在的直线为轴,建立平面直角坐标系,证明三点不共线请你帮小红完成证明;(2)、如图,将正方形沿图中虚线剪成四块图形其中 , 用这四块图形恰能拼成一个矩形非正方形 , 求的值.四、理论探究题
-
16. 问题提出:
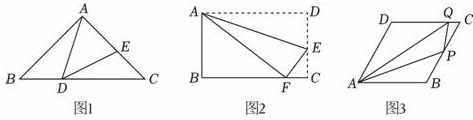 (1)、如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC , 点D、E分别在边BC、AC上,连接AD、DE , 有∠ADE=45°.求证:△BDA∽△CED;(2)、问题探究
(1)、如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC , 点D、E分别在边BC、AC上,连接AD、DE , 有∠ADE=45°.求证:△BDA∽△CED;(2)、问题探究如图2,将矩形ABCD沿AE折叠,使点D落在BC边的点F处,若AB=3,AD=5,求DE的长;
(3)、问题解决如图3,菱形ABCD是一座避暑山庄的平面示意图,其中∠BAD=60°,AB=120米,现计划在山庄内修建一个三角形花园AP , 点P、Q分别在线段BC、CD上,根据设计要求要使∠APQ=120°,且AP=3PQ , 问能否建造出符合要求的三角形花园APQ , 若能,请找出点P、Q的位置(即求出DQ与BP的长),若不能,请说明理由.
17. 问题背景: 一次数学综合实践活动课上, 小致发现并证明了关于三角形角平分线的一个结论. 如图①, 已知 A D 是 的角平分线, 可证 . 小致的证明思路是:如图②, 过点 作 , 交 A D 的延长线于点 , 构造相似三角形来证明. (1)、尝试证明: 请参照小致的思路, 利用图②证明 .(2)、基础训练:如图③,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将
(1)、尝试证明: 请参照小致的思路, 利用图②证明 .(2)、基础训练:如图③,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的E点处.若AC=1,AB=2,则DE的长为
(3)、拓展升华:如图④,△ABC中,AB=6,AC=4,AD平分∠BAC,AD的中垂线EF交BC延长线于点F,当BD=3时,AF= .18. 阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,那么我们就把点E叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,那么我们就把点E叫四边形ABCD的边AB上的“强相似点”.
解决问题:
(1)、如图1,∠A=∠B=∠DEC=50°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由.(2)、如图2,在矩形ABCD中,A,B,C,D四点均在正方形网格(网格中每个小正方形的边长均为1)的格点(即每个小正方形的顶点)上,试在图中画出矩形ABCD的边AB上的强相似点.(3)、如图3,将矩形ABCD沿着CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.19. 某“数学学习兴趣小组”成员在复习《图形的变化》时,对下面的图形背景产生了浓厚的兴趣,并尝试运用由“特殊到一般”的思想进行了探究:
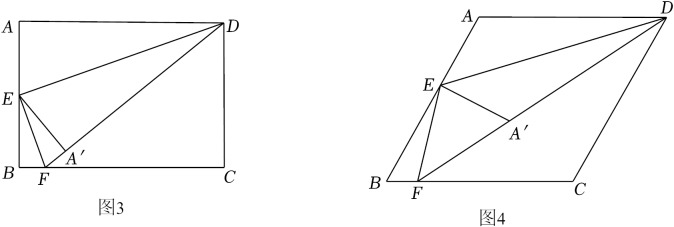 (1)、【问题背景】如图1,正方形ABCD中,点E为AB边上一点,连接DE , 过点E作EF⊥DE交BC边于点F , 将△ADE沿直线DE折叠后,点A落在点A'处,当∠BEF=25°,则∠FEA'=°.(2)、【特例探究】如图2,连接DF , 当点A'恰好落在DF上时,求证:AE=2A'F .(3)、【深入探究】如图3,若把正方形ABCD改成矩形ABCD , 且AD=mAB , 其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.(4)、【拓展探究】如图4,若把正方形ABCD改成菱形ABCD , 且∠B=60°,∠DEF=120°,其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.20. 定义:长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.
(1)、【问题背景】如图1,正方形ABCD中,点E为AB边上一点,连接DE , 过点E作EF⊥DE交BC边于点F , 将△ADE沿直线DE折叠后,点A落在点A'处,当∠BEF=25°,则∠FEA'=°.(2)、【特例探究】如图2,连接DF , 当点A'恰好落在DF上时,求证:AE=2A'F .(3)、【深入探究】如图3,若把正方形ABCD改成矩形ABCD , 且AD=mAB , 其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.(4)、【拓展探究】如图4,若把正方形ABCD改成菱形ABCD , 且∠B=60°,∠DEF=120°,其他条件不变,他们发现AE与A′F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.20. 定义:长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.操作1:将正方形沿过点的直线折叠,使折叠后的点落在对角线上的点处,折痕为 .
操作2:将沿过点的直线折叠,使点 , 点分别落在边 , 上,折痕为 .
则四边形为矩形.
证明:设正方形的边长为1,则 .
由折叠性质可知 , , 则四边形为矩形,
∴ , ∴ .
∴ , 即 , ∴ , ∴ ,
∴四边形为矩形.

阅读以上内容,回答下列问题:
(1)、在图①中,所有与相等的线段是、 , 的值是;(2)、已知四边形为矩形,模仿上述操作,得到四边形 , 如图②,求证:四边形为矩形;(3)、将图②中的矩形沿用(2)中的方式操作3次后,得到一个“矩形”,则的值是 .21. 【提出问题】如图 , 在等腰中, , 分别以 , 为边作等边和等边 , 与相交于点 , 连接 .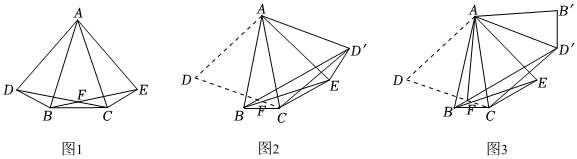 (1)、【初步探究】如图 , 连接 , 求证:≌ .(2)、【深入探究】如图 , 将沿翻折得到 , 连接 , , 类比的探究方法发现:
(1)、【初步探究】如图 , 连接 , 求证:≌ .(2)、【深入探究】如图 , 将沿翻折得到 , 连接 , , 类比的探究方法发现:
结论:_▲_≌;
结论: .
请证明结论 .(3)、如图、在的情况下将线段沿翻折得到线段 , 连接 , , 试判断线段与的位置关系.22. 综合与实践在一次综合实践活动课上,王老师给每位同学各发了一张正方形纸片,请同学们思考如何仅通过折纸的方法来确定正方形一边上的一个三等分点.


【操作探究】
“乘风”小组的同学经过一番思考和讨论交流后,进行了如下操作:
第1步:如图1所示,先将正方形纸片ABCD对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:将BC边沿CE翻折到GC的位置;
第3步:延长EG交AD于点H,则点H为AD边的三等分点.
证明过程如下:连接CH,
∵正方形ABCD沿CE折叠,
∴∠D=∠B=∠CGH=90°, ① ,
又∵CH=CH
∴△CGH≌△CDH,
∴GH=DH.
由题意可知E是AB的中点,设AB=6(个单位),DH=x,则AE=BE=EG=3,
在Rt△AEH中,可列方程: ② , (方程不要求化简)解得:DH= ③ , 即H是AD边的三等分点.
“破浪”小组是这样操作的:
第1步:如图2所示,先将正方形纸片对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:再将正方形纸片对折,使点B与点D重合,再展开铺平,折痕为AC,沿DE翻折得折痕DE交AC于点G;
第3步:过点G折叠正方形纸片ABCD,使折痕MNIIAD.
【过程思考】
(1)、“乘风”小组的证明过程中,三个空的所填的内容分别是: ① , ②: , ③: ;(2)、结合“破浪”小组操作过程,判断点M是否为AB边的三等分点,并证明你的结论;(3)、【拓展提升】如图3,在菱形ABCD中,AB=5,BD=6,E是BD上的一个三等分点,记点D关于AE的对称点为D',射线ED'与菱形ABCD 的边交于点F,请直接写出D'F的长.23.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证: (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中, , 为边上的三等分点,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中, , 为边上的三等分点,将沿翻折得到 , 直线交于点求的长. 24. 综合与实践
24. 综合与实践 (1)、【操作发现】如图1,诸葛小组将正方形纸片ABCD沿过点A的直线折叠,使点B落在正方形内部的点M处,折痕为AE , 再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF , 求∠EAF的正切值;(2)、【拓展探究】如图2,孔明小组继续将正方形纸片沿EF继续折叠,点C的对应点恰好落在折痕AE上的点N处,连接NF交AM于点P , 若 , 求线段PM的长;(3)、【迁移应用】如图3,在矩形ABCD中,点E , F分别在边BC , CD上,将矩形ABCD沿AE , AF折叠,点B落在点M处,点D落在点G处,点A , M , G恰好在同一直线上,若点F为CD的三等分点,AB=3,AD=5,请求出线段BE的长.25. 如图
(1)、【操作发现】如图1,诸葛小组将正方形纸片ABCD沿过点A的直线折叠,使点B落在正方形内部的点M处,折痕为AE , 再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF , 求∠EAF的正切值;(2)、【拓展探究】如图2,孔明小组继续将正方形纸片沿EF继续折叠,点C的对应点恰好落在折痕AE上的点N处,连接NF交AM于点P , 若 , 求线段PM的长;(3)、【迁移应用】如图3,在矩形ABCD中,点E , F分别在边BC , CD上,将矩形ABCD沿AE , AF折叠,点B落在点M处,点D落在点G处,点A , M , G恰好在同一直线上,若点F为CD的三等分点,AB=3,AD=5,请求出线段BE的长.25. 如图
[问题背景]
如图1.数学实践课上,学习小组进行探究活动,老师要求大家对矩形ABCD进行如下操作;①分别以点B. C 为圆心,以大于BC的长度为半径作弧,两弧相交于点E、F,作真线EF交BC于点O.连接AO;②将△ABO沿AO翻折,点B的对应点落在点P处,作射线AP交CD于点Q.
[问题提出]
在矩形ABCD中,AD=5,AB=3,求线段CQ的长:
[问题解决]
经过小组合作、探究、展示,其中的两个方案如下:
方案一:连按OQ,如图2.经过推理、计算可求出线段CQ的长:
方案二:将△ABO绕点O旋转180°至△RCO处,如图3.经过推理、计算可求出线段CQ的长.
请你任选其中一种方案求线段CQ的长.
26. (1)、【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:
(1)、【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:如图①,在矩形中, , 分别交于点E、F,分别交于点G、H,求证:;
(2)、【结论应用】如图②,将矩形沿折叠,使得点B和点D重合,若 , 求折痕的长;(3)、【拓展运用】如图③,将矩形沿折叠.使得点D落在边上的点G处,点C落在点P处,得到四边形 , 若 , 求的长.27. 综合与实践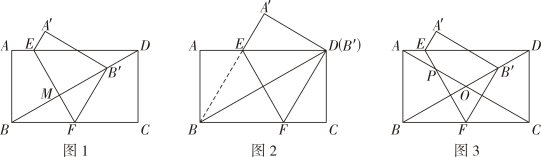
[问题情境]
如图1,小华将矩形纸片ABCD先沿对角线BD折叠,展开后再折叠,使点B落在对角线BD上,点B的对应点记为B',折痕与边AD,BC分别交于点E,F.
(1)、 [活动猜想]如图2,当点B'与点D重合时,四边形BEDF是哪种特殊的四边形?并给予证明.(2)、 [问题解决]如图1,当AB=4, AD=8,BF=3时,连结B'C,则B'C的长为(3)、 [深入探究]如图3,请直接写出AB与BC满足什么关系时,始终有A'B'与对角线AC平行?28. 问题背景:一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图①,已知AD是△ABC的角平分线,可证 . 小慧的证明思路是:如图②,过点C作CE∥AB,交AD的延长线于点E,构造相似三角形来证明.
 (1)、尝试证明:请参照小慧的思路,利用图②证明(2)、基础训练:如图③,在Rt△ABC中,∠BAC=90°,D足边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB.上的E点处,若AC=1,AB=2,则DE的长为(3)、拓展升华:如图④,△ABC中,AB=6,AC=4, AD平分∠BAC,AD的中垂线EF交BC延长线于点F,当BD= 时,AF=29.
(1)、尝试证明:请参照小慧的思路,利用图②证明(2)、基础训练:如图③,在Rt△ABC中,∠BAC=90°,D足边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB.上的E点处,若AC=1,AB=2,则DE的长为(3)、拓展升华:如图④,△ABC中,AB=6,AC=4, AD平分∠BAC,AD的中垂线EF交BC延长线于点F,当BD= 时,AF=29. (1)、【探究问题】阅读并补全解题过程
(1)、【探究问题】阅读并补全解题过程
如图 , 在四边形中, , 点是边的中点, , 求证:平分 .
张某某同学受到老师说过的“有中点,延长加倍构造全等”的启发,延长交射线于点 , 请你依据该同
学的做法补全证明过程.
证明:延长交射线于点 .(2)、【应用】如图 , 在长方形中,将沿直线折叠,若点恰好落在边的中点处,直接写出的度数;
(3)、【拓展】如图 , 在正方形中,为边的中点,将沿直线折叠,点落在正方形内部的点处,延长交于点 , 延长交于点 , 若正方形的边长为 , 直接写出的值.