备考2024年中考数学探究性训练专题20 四边形
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 我们在探究“任意一个四边形内角和是多少度?”时,采用的方法是连接四边形的一条对角线,把四边形分割成两个三角形,从而探究出任意四边形的内角和等于360°,这一过程体现的数学思想是( )A、转化思想 B、方程思想 C、函数思想 D、数形结合思想2. 对于一元二次方程,我国古代数学家还研究过其几何解法.以方程为例加以说明.数学家赵爽在其所著的《勾股圆方注》中记载的方法是:如图,将四个长为 , 宽为的长方形纸片拼成一个大正方形,则大正方形的边长是 , 面积是四个矩形的面积与中间小正方形的面积之和,即 , 据此易得 . 小明用此方法解关于的方程 , 其中构造出同样的图形,已知小正方形的面积为4,则的值为( )
 A、2 B、4 C、6 D、83. 在《类比探究菱形的有关问题》这节网课中,老师给出了如下画菱形的步骤,请问这么画的依据是( )
A、2 B、4 C、6 D、83. 在《类比探究菱形的有关问题》这节网课中,老师给出了如下画菱形的步骤,请问这么画的依据是( )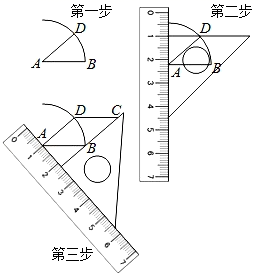 A、四条边都相等的四边形是菱形 B、两组对边分别相等的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 C、两组对边分别平行的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 D、两组对边分别平行的四边形是平行四边形,两条对角线互相垂直的平行四边形是菱形4. 数学家莫伦在年发现了世界上第一个完美长方形(如图),即它恰好能被分割成个大小不同的正方形,从这以后人们开始热衷图形完美分割的研究,平行四边形被分割成个小正三角形(如图2),已知中间最小的两个正三角形和边长均为 , 平行四边形的周长为( )
A、四条边都相等的四边形是菱形 B、两组对边分别相等的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 C、两组对边分别平行的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 D、两组对边分别平行的四边形是平行四边形,两条对角线互相垂直的平行四边形是菱形4. 数学家莫伦在年发现了世界上第一个完美长方形(如图),即它恰好能被分割成个大小不同的正方形,从这以后人们开始热衷图形完美分割的研究,平行四边形被分割成个小正三角形(如图2),已知中间最小的两个正三角形和边长均为 , 平行四边形的周长为( )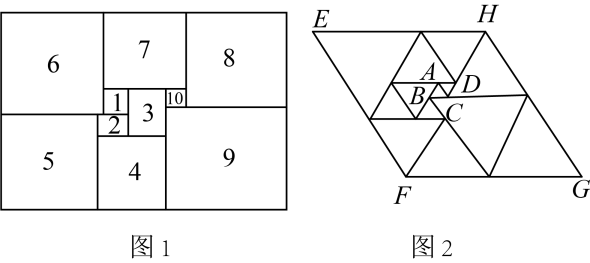 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
5. 如图是跷跷板的示意图,立柱 与地面垂直,以 为横板 的中点, 绕点 上下转动,横板 的 端最大高度 是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设 , ,通过计算得到此时的 ,再将横板 换成横板 , 为横板 的中点,且 ,此时 点的最大高度为 ,由此得到 与 的大小关系是: (填“ 、“ ”或“ ”)可进一步得出, 随横板的长度的变化而(填“不变”或“改变”).
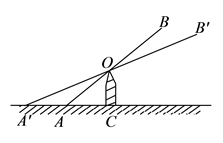 6. 在图1所示的 的网格内有一个八边形,其中每个小方格的边长均为1.经探究发现,此八边形可按图2的方式分割成四个全等的五边形和一个小正方形①.现将分割后的四个五边形重新拼接(即图2中的阴影部分),得到一个大正方形 ,发现该正方形中间的空白部分②也是一个正方形,且正方形②的面积恰好是正方形①的面积的2倍,则 的长为.
6. 在图1所示的 的网格内有一个八边形,其中每个小方格的边长均为1.经探究发现,此八边形可按图2的方式分割成四个全等的五边形和一个小正方形①.现将分割后的四个五边形重新拼接(即图2中的阴影部分),得到一个大正方形 ,发现该正方形中间的空白部分②也是一个正方形,且正方形②的面积恰好是正方形①的面积的2倍,则 的长为. 7. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,是矩形的对角线,将分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若 , 则矩形的面积是 .
7. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,是矩形的对角线,将分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若 , 则矩形的面积是 . 8. 何老师在一次“探析矩形折叠问题”的公开课上,与同学们一起对折纸进行了如下探究:已知正方形边长为1,G是边的中点,E是射线上的一个动点.
8. 何老师在一次“探析矩形折叠问题”的公开课上,与同学们一起对折纸进行了如下探究:已知正方形边长为1,G是边的中点,E是射线上的一个动点. (1)、如图① ,若点E在线段上且点E与点C不重合,连结 , 将沿着翻折,使点C落在上的点M处,连结延长交边于点F且 , 则的值为(2)、若点E与点C不重合,以点C为圆心,线段的长为半径作 , 当与线段只有一个公共点时,的取值范围是.9. 综合实践课上,小聪用一张长方形纸ABCD对不同折法下的折痕进行了探究,已知AB=12,∠CAB=30°,点E,F分别在AB,CD上,且AE=5,
(1)、如图① ,若点E在线段上且点E与点C不重合,连结 , 将沿着翻折,使点C落在上的点M处,连结延长交边于点F且 , 则的值为(2)、若点E与点C不重合,以点C为圆心,线段的长为半径作 , 当与线段只有一个公共点时,的取值范围是.9. 综合实践课上,小聪用一张长方形纸ABCD对不同折法下的折痕进行了探究,已知AB=12,∠CAB=30°,点E,F分别在AB,CD上,且AE=5, (1)、把长方形纸片沿着直线EF翻折,使点A的对应点A′恰好落在对角线AC上,点D的对应点为D′,如图①,则折痕EF长为 ;(2)、在EF,A′D′上取点G,H,沿着直线GH继续翻折,使点E与点F重合,如图②,则折痕GH长为 .10. 如图,某数学兴趣小组在学完矩形的知识后一起探讨了一个纸片折叠问题:如何将一张平行四边形纸片 的四个角向内折起,拼成一个无缝隙、无重叠的矩形 .图中 , , , 表示折痕,折后 的对应点分别是 .若 , , ,则纸片折叠时 的长应取 .
(1)、把长方形纸片沿着直线EF翻折,使点A的对应点A′恰好落在对角线AC上,点D的对应点为D′,如图①,则折痕EF长为 ;(2)、在EF,A′D′上取点G,H,沿着直线GH继续翻折,使点E与点F重合,如图②,则折痕GH长为 .10. 如图,某数学兴趣小组在学完矩形的知识后一起探讨了一个纸片折叠问题:如何将一张平行四边形纸片 的四个角向内折起,拼成一个无缝隙、无重叠的矩形 .图中 , , , 表示折痕,折后 的对应点分别是 .若 , , ,则纸片折叠时 的长应取 .
三、实践探究题
-
11. 综合与探究
如图,经过 , 两点的抛物线与轴的另一个交点为 .
 (1)、求抛物线的解析式;(2)、点在抛物线的对称轴上,当的周长最小时,求的坐标;(3)、已知点在抛物线上,求时的点坐标;(4)、已知 , 请直接写出能以点 , , , 为顶点的四边形是平行四边形的点坐标.12.
(1)、求抛物线的解析式;(2)、点在抛物线的对称轴上,当的周长最小时,求的坐标;(3)、已知点在抛物线上,求时的点坐标;(4)、已知 , 请直接写出能以点 , , , 为顶点的四边形是平行四边形的点坐标.12.

【问题】北师大版数学八年级下册P32第2题:
已知:如图1,的外角和的平分线相交于点F.
求证:点F在的平分线上.
某数学兴趣小姐的小明同学提出了如下的解题方法:
如图2,过点F作于点G,作于点H,作于点M,由角平分线的性质定理可得: , .
∴ .
∵ , ,
∴F在的平分结上.


【探究】
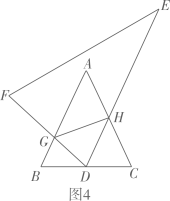
(1)、小方在研究小明的解题过程时,还发现图2中和三条线段存在一定的数量关系,请你直接写出它们的数量关系:;(2)、小明也发现和之间存在一定的数量关系.请你直接写出它们的数量关系:;(3)、如图3,边长为3的正方形中,点E,F分别是边上的点,且 . 连接 , 若 , 求的长;(4)、如图4,中, , . 中, . 将的顶点D放在边的中点处,边交线段于点G,边交线段于点H,连接 . 现将绕着点D旋转,在旋转过程中,的周长是否发生变化?若不变,求出的周长,若改变,请说明理由.13. 小星和小红在学习了正方形的相关知识后,对正方形内一些特殊线段的关系进行探究.

 (1)、问题解决
(1)、问题解决如图(1)所示,在正方形ABCD中,E,F分别是BC,CD边上的点,连接AE,BF,且AE⊥BF,求证:△ABE≌△BCF;
(2)、类比探究如图(2)所示,在正方形ABCD中,E,F,G,H分别是BC,AD,AB,CD边上的点,连接EF,GH,且EF⊥GH,求证:EF=GH;
(3)、迁移应用如图(3)所示,在Rt△ABC中,∠ABC=90°,AB=BC,D是BC的中点,E是AC边上的点,连接AD,BE,且BE⊥AD,求AE∶CE的值.
14. 某校数学活动小组探究了如下数学问题:
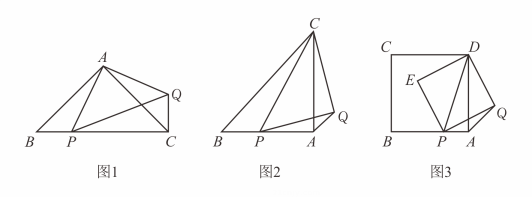 (1)、问题发现:如图 , 中, , 点是底边上一点,连接 , 以为腰作等腰 , 且 , 连接、则和的数量关系是 ;(2)、变式探究:如图 , 中, , 点是腰上一点,连接 , 以为底边作等腰 , 连接 , 判断和的数量关系,并说明理由;(3)、问题解决;如图 , 正方形的边长为 , 点是边上一点,以为对角线作正方形 , 连接若设正方形的面积为 , 求与的函数关系式.15. [探究与证明]折纸,操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘.
(1)、问题发现:如图 , 中, , 点是底边上一点,连接 , 以为腰作等腰 , 且 , 连接、则和的数量关系是 ;(2)、变式探究:如图 , 中, , 点是腰上一点,连接 , 以为底边作等腰 , 连接 , 判断和的数量关系,并说明理由;(3)、问题解决;如图 , 正方形的边长为 , 点是边上一点,以为对角线作正方形 , 连接若设正方形的面积为 , 求与的函数关系式.15. [探究与证明]折纸,操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘.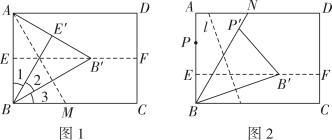
[动手操作]如图1,将矩形纸片ABCD对折,使AD与BC重合,展平纸片,得到折痕EF;折叠纸片,使点B落在EF.上,并使折痕经过点A,得到折痕AM.点B,E的对应点分别为B',E',展平纸片,连结AB',BB',BE'.请完成:
(1)、观察图1中∠1,∠2和∠3,试猜想这三个角的大小关系.(2)、证明(1)中的猜想.(3)、[类比操作]如图2,N为矩形纸片ABCD的边AD上的一点,连结BN,在AB上取一点P,折叠纸片,使B,P两点重合,展平纸片,得到折痕EF;折叠纸片,使点B,P分别落在EF,BN上,得到折痕l,点B,P的对应点分别为B',P',展平纸片,连结BB',P'B'.请完成:证明BB'是∠NBC的一条三等分线.
16. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<a≤90°)得到矩形AB'C'D',连结BD.. (1)、【探究1】如图1,当α=90°时,点C'恰好在DB的延长线上.若AB=1,求BC的长.(2)、【探究2】如图2,连结AC,过点D'作D'M //AC'交BD于点M.线段D'M 与 DM 相等吗?请说明理由.(3)、【探究3】在探究2的条件下,射线DB分别交AD',AC'于点P,N(如图3),发现线段DN,MN,PN之间存在一定的数量关系,请写出这个关系式,并加以证明.17. 【探究与证明】
(1)、【探究1】如图1,当α=90°时,点C'恰好在DB的延长线上.若AB=1,求BC的长.(2)、【探究2】如图2,连结AC,过点D'作D'M //AC'交BD于点M.线段D'M 与 DM 相等吗?请说明理由.(3)、【探究3】在探究2的条件下,射线DB分别交AD',AC'于点P,N(如图3),发现线段DN,MN,PN之间存在一定的数量关系,请写出这个关系式,并加以证明.17. 【探究与证明】折纸,操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘.
【动手操作】如图1,将矩形纸片对折,使与重合,展平纸片,得到折痕;折叠纸片,使点B落在上,并使折痕经过点A,得到折痕 , 点B,E的对应点分别为 , , 展平纸片,连接 , , .

请完成:
(1)、观察图1中 , 和 , 试猜想这三个角的大小关系;(2)、证明(1)中的猜想;【类比操作】如图2,N为矩形纸片的边上的一点,连接 , 在上取一点P,折叠纸片,使B,P两点重合,展平纸片,得到折痕;折叠纸片,使点B,P分别落在 , 上,得到折痕l,点B,P的对应点分别为 , , 展平纸片,连接, .
 (3)、证明是的一条三等分线.18. 【问题情境】:
(3)、证明是的一条三等分线.18. 【问题情境】:数学活动课上,同学们开展了以折叠为主题的探究活动,如图1,已知矩形纸片 , 其中宽 .
 (1)、【动手实践】:
(1)、【动手实践】:如图1,威威同学将矩形纸片折叠,点落在边上的点处,折痕为 , 连接 , 然后将纸片展平,得到四边形 , 则折痕的长度为 .
(2)、【探究发现】:如图2,胜胜同学将图1中的四边形剪下,取边中点 , 将沿折叠得到 , 延长交于点 . 点为边的中点,点是边上一动点,将沿折叠,当点的对应点落在线段上时,求此时的值;
(3)、【反思提升】:明明同学改变图2中点的位置,即点为边上一动点,点仍是边上一动点,按照(2)中方式折叠 , 使点落在线段上,明明同学不断改变点的位置,发现在某一位置与(2)中的相等,请直接写出此时的长度.
19. 某数学兴趣小组在数学课外活动中,对矩形内两条互相垂直的线段做了如下探究: (1)、 [观察与猜想]
(1)、 [观察与猜想]如图①,在正方形中,点E、F分别是、上的两点,连接、 , , 则的值为=;
(2)、如图②,在矩形中, , , 点E是上的一点,连接 , , 且 , 则的值为 .(3)、 [性质探究]如图③,在四边形中, . 点E为上一点,连接 , 过点C作的垂线交的延长线于点G,交的延长线于点F.求证:;
(4)、[拓展延伸]已知四边形是矩形, ,如图④,点P是上的点,过点P作 , 垂足为O,点O恰好落在对角线上.求的值;
(5)、如图⑤,点P是上的一点,过点P作 , 垂足为O,点O恰好落在对角线上,延长、交于点G.当时, .20. 问题提出
如图(1),E是菱形ABCD边BC上一点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°),AF交CD于点G,探究∠GCF与α的数量关系. (1)、问题探究
(1)、问题探究先将问题特殊化,如图(2),当α=90°,直接写出∠GCF的大小;
(2)、再探究一般情形,如图(1),求∠GCF与α的数量关系.问题拓展
将图(1)特殊化,如图(3),当α=120°,若 , 求的值.21. 综合与探究问题情境:数学课上,老师引导同学们以“正方形中线段的旋转”为主题开展数学活动.已知正方形ABCD中, , 点E是射线CD上一点(不与点C重合),连接BE , 将BE绕点E顺时针旋转得到FE , 连接DF.
 (1)、特例分析:如图1,当点E与点D重合时,求的度数;(2)、深入谈及:当点E不与点D重合时,(1)中的结论是否仍然成立?若成立,请在图2与图3中选择一种情况进行证明;若不成立,请说明理由;(3)、问题解决:如图4,当点E在线段CD上,且时,请直接写出线段BF的长.22. 小明学习了平行四边形这一章后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
(1)、特例分析:如图1,当点E与点D重合时,求的度数;(2)、深入谈及:当点E不与点D重合时,(1)中的结论是否仍然成立?若成立,请在图2与图3中选择一种情况进行证明;若不成立,请说明理由;(3)、问题解决:如图4,当点E在线段CD上,且时,请直接写出线段BF的长.22. 小明学习了平行四边形这一章后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形. (1)、概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是(2)、性质探究:通过探究,直接写出垂直四边形ABCD的面积S与两对角线AC,BD之间的数量关系: .(3)、问题解决:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CG,BE,GE,已知AC=4,AB=5.
(1)、概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是(2)、性质探究:通过探究,直接写出垂直四边形ABCD的面积S与两对角线AC,BD之间的数量关系: .(3)、问题解决:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CG,BE,GE,已知AC=4,AB=5.①求证:四边形BCGE为垂美四边形;
②求出四边形BCGE的面积.
23. 综合与实践问题情境:数学课上,同学们以特殊四边形为基本图形,添加一些几何元素后探究图形中存在的结论.已知在□ABCD中,AB<BC,∠ABC的平分线交AD边于点E,交CD边的延长线于点F,以DE,DF为邻边作□DEGF.
 (1)、 特例探究:如图1,“创思”小组的同学研究了四边形ABCD为矩形时的情形,发现四边形DEGF是正方形,请你证明这一结论;(2)、“敏学”小组的同学在图1基础上连接BG,AC,得到图2,发现图2中线段BG与AC之间存在特定的数量关系,请你帮他们写出结论并说明理由;(3)、 拓展延伸:“善问"小组的同学计划对□ABCD展开类似研究.如图3,在□ABCD中,∠ABC=60.
(1)、 特例探究:如图1,“创思”小组的同学研究了四边形ABCD为矩形时的情形,发现四边形DEGF是正方形,请你证明这一结论;(2)、“敏学”小组的同学在图1基础上连接BG,AC,得到图2,发现图2中线段BG与AC之间存在特定的数量关系,请你帮他们写出结论并说明理由;(3)、 拓展延伸:“善问"小组的同学计划对□ABCD展开类似研究.如图3,在□ABCD中,∠ABC=60.请从下面 , 两题中任选一题作答.我选择 ▲ 题.
:当AB=4,BC=6时,请补全图形,并直接写出A,G两点之间的距离.
:当BC=6时,请补全图形,并直接写出以A,C,G为顶点的三角形面积的最小值.
24. 通过以前的学习,我们知道:“如图1,在正方形中, , 则”. 某数学兴趣小组在完成了以上学习后,决定对该问题进一步探究: (1)、【问题探究】如图2,在正方形中,点 , , , 分别在线段 , , , 上,且 , 试猜想;(2)、【知识迁移】如图3,在矩形中, , , 点 , , , 分别在线段 , , , 上,且 , 试猜想的值,并证明你的猜想;(3)、【拓展应用】如图4,在四边形中, , , , 点 , 分别在线段 , 上,且 , 求的值.25. 在数学活动课上,老师让同学们以“三角形纸片的折叠、旋转”为主题开展数学活动,探究与角的度数、线段长度有关的问题.对直角三角形纸片进行如下操作:
(1)、【问题探究】如图2,在正方形中,点 , , , 分别在线段 , , , 上,且 , 试猜想;(2)、【知识迁移】如图3,在矩形中, , , 点 , , , 分别在线段 , , , 上,且 , 试猜想的值,并证明你的猜想;(3)、【拓展应用】如图4,在四边形中, , , , 点 , 分别在线段 , 上,且 , 求的值.25. 在数学活动课上,老师让同学们以“三角形纸片的折叠、旋转”为主题开展数学活动,探究与角的度数、线段长度有关的问题.对直角三角形纸片进行如下操作: (1)、【初步探究】
(1)、【初步探究】如图1,折叠三角形纸片 , 使点C与点A重合,得到折痕 , 然后展开铺平,则与位置关系为 , 与的数量关系为;
(2)、【再次探究】如图2,将绕点C顺时针旋转得到 , 连接 , 若 , 求的值;
(3)、【拓展提升】在(2)的条件下,在顺时针旋转一周的过程中,当时,求的长.
26. 综合与探究:如图,直线:与直线:交于点 , 直线与轴交于点 , 点从点出发沿向终点运动,速度为每秒个单位,同时点从点出发以同样的速度沿向终点运动,作轴,交折线于点 , 作轴,交折线于点 , 设运动时间为 .
 (1)、求 , 点的坐标;(2)、在点 , 点运动过程中,
(1)、求 , 点的坐标;(2)、在点 , 点运动过程中,当点 , 分别在 , 上时,求证四边形是矩形;
在点 , 点的整个运动过程中,当四边形是正方形时,请你直接写出的值;
(3)、点是平面内一点,在点的运动过程中,问是否存在以点 , , , 为顶点的四边形是菱形,若存在,请直接写出点的坐标,若不存在,请说明理由.27. 一张矩形纸片ABCD(如图1),AB=6,AD=3.点E是BC边上的一个动点,将△ABE沿直线AE折叠得到△AEF,延长AE交直线CD于点G,直线AF与直线CD交于点Q.
【初步探究】
(1)、求证:△AQG是等腰三角形;(2)、记FQ=m,当BE=2CE时,计算m的值;(3)、【深入探究】
将矩形纸片放入平面直角坐标系中(如图2所示),点B与点O重合,边OC、OA分别与x轴、y轴正半轴重合.点H在OC边上,将△AOH沿直线AH折叠得到△APH.①当AP经过CD的中点N时,求点P的坐标;
②在①的条件下,已知二次函数y=-x2+bx+c的图象经过A、D两点.若将直线AH右侧的抛物线沿AH对折,交y轴于点M,请求出AM的长度.28. 【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
 (1)、判断△AFG的形状并说明理由.(2)、求证:BF=2OG.(3)、【迁移应用】
(1)、判断△AFG的形状并说明理由.(2)、求证:BF=2OG.(3)、【迁移应用】
记△DGO的面积为S1 , △DBF的面积为S2 , 当时,求的值.(4)、【拓展延伸】
若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.29. 某“数学学习兴趣小组”成员在复习《图形的变化》时,对下面的图形背景产生了浓厚的兴趣,并尝试运用由“特殊到一般”的思想进行了探究:(1)、【问题背景】如图1,正方形ABCD中,点E为AB边上一点,连接DE,过点E作EF⊥DE交BC边于点F,将△ADE沿直线DE折叠后,点A落在点 处,当∠BEF=25°,则∠FE =°. (2)、【特例探究】如图2,连接DF,当点 恰好落在DF上时,求证:AE=2 F.
(2)、【特例探究】如图2,连接DF,当点 恰好落在DF上时,求证:AE=2 F. (3)、【深入探究】若把正方形ABCD改成矩形ABCD,且AD=mAB,其他条件不变,他们发现AE与 F之间也存在着一定的数量关系,请直接写出AE与 F之间的数量关系式.
(3)、【深入探究】若把正方形ABCD改成矩形ABCD,且AD=mAB,其他条件不变,他们发现AE与 F之间也存在着一定的数量关系,请直接写出AE与 F之间的数量关系式. (4)、【拓展探究】若把正方形ABCD改成菱形ABCD,且∠B=60°,∠DEF=120°,其他条件不变,他们发现AE与 F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.30. 如图1,小丽借助几何软件进行数学探究:第一步,画出矩形和矩形 , 点、在边上(),且点、、、在直线的同侧;第二步,设置 , 矩形能在边上左右滑动;第三步,画出边的中点 , 射线与射线相交于点(点、不重合),射线与射线相交于点(点、不重合),观测、的长度.
(4)、【拓展探究】若把正方形ABCD改成菱形ABCD,且∠B=60°,∠DEF=120°,其他条件不变,他们发现AE与 F之间也存在着一定的数量关系,请直接写出AE与A′F之间的数量关系式.30. 如图1,小丽借助几何软件进行数学探究:第一步,画出矩形和矩形 , 点、在边上(),且点、、、在直线的同侧;第二步,设置 , 矩形能在边上左右滑动;第三步,画出边的中点 , 射线与射线相交于点(点、不重合),射线与射线相交于点(点、不重合),观测、的长度.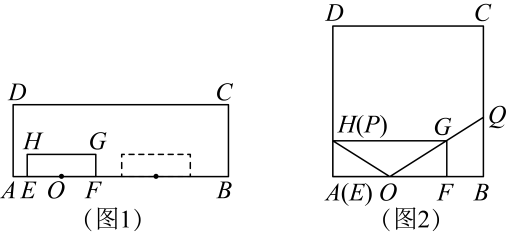 (1)、如图 , 小丽取 , 滑动矩形 , 当点、重合时,;(2)、小丽滑动矩形 , 使得恰为边的中点.她发现对于任意的总成立.请说明理由;(3)、经过数次操作,小丽猜想,设定、的某种数量关系后,滑动矩形 , 总成立.小丽的猜想是否正确?请说明理由.
(1)、如图 , 小丽取 , 滑动矩形 , 当点、重合时,;(2)、小丽滑动矩形 , 使得恰为边的中点.她发现对于任意的总成立.请说明理由;(3)、经过数次操作,小丽猜想,设定、的某种数量关系后,滑动矩形 , 总成立.小丽的猜想是否正确?请说明理由.