备考2024年中考数学探究性训练专题19 三角形
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如已知△ABC中,∠A=30°, AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( )
 A、 B、 C、或 D、或2. 数学课上老师布置了“测量锥形瓶内部底面的内径”的探究任务,善思小组想到了以下方案:如图,用螺丝钉将两根小棒 , 的中点O固定,只要测得C,D之间的距离,就可知道内径 的长度.此方案依据的数学定理或基本事实是( )
A、 B、 C、或 D、或2. 数学课上老师布置了“测量锥形瓶内部底面的内径”的探究任务,善思小组想到了以下方案:如图,用螺丝钉将两根小棒 , 的中点O固定,只要测得C,D之间的距离,就可知道内径 的长度.此方案依据的数学定理或基本事实是( ) A、边角边 B、三角形中位线定理 C、边边边 D、全等三角形的对应角相等3. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘B处离桌面的高度为 , 此时底部边缘A处与C处间的距离为 , 小组成员调整张角的大小继续探究,最后发现当张角为时(D是B的对应点),顶部边缘D处到桌面的距离为 , 则底部边缘A处与E之间的距离为( )
A、边角边 B、三角形中位线定理 C、边边边 D、全等三角形的对应角相等3. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘B处离桌面的高度为 , 此时底部边缘A处与C处间的距离为 , 小组成员调整张角的大小继续探究,最后发现当张角为时(D是B的对应点),顶部边缘D处到桌面的距离为 , 则底部边缘A处与E之间的距离为( )
 A、 B、 C、 D、4. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中 , , 在探究筝形的性质时,得到如下结论:
A、 B、 C、 D、4. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中 , , 在探究筝形的性质时,得到如下结论:
;;≌ ,
其中正确的结论有( )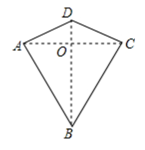 A、个 B、个 C、个 D、个5. 某兴趣小组开展综合实践活动:在中, , 为上一点,动点以每秒1个单位的速度从点出发,在三角形边上沿匀速运动,到达点时停止,以为边作正方形 , 设点的运动时间为 , 正方形的面积为 , 当点由点运动到点时,经探究发现是关于的二次函数,并绘制成如图2所示的图象,若存在3个时刻对应的正方形DPEF的面积均相等,当时,则正方形的面积为( )
A、个 B、个 C、个 D、个5. 某兴趣小组开展综合实践活动:在中, , 为上一点,动点以每秒1个单位的速度从点出发,在三角形边上沿匀速运动,到达点时停止,以为边作正方形 , 设点的运动时间为 , 正方形的面积为 , 当点由点运动到点时,经探究发现是关于的二次函数,并绘制成如图2所示的图象,若存在3个时刻对应的正方形DPEF的面积均相等,当时,则正方形的面积为( )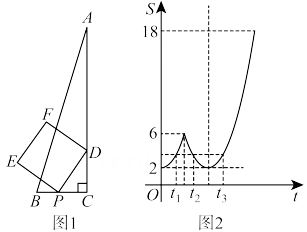 A、3 B、 C、4 D、5
A、3 B、 C、4 D、5二、填空题
-
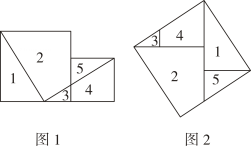
6. 【动手实践】小明学习了课本“实验与探究”后做了如下探索:他按图1方法把边长为5厘米和3厘米的两个正方形切割成5块,按图2方式拼成的一个大正方形,则大正方形的边长是厘米.
 7. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知中, , , 所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的是一个直角三角形),则满足已知条件的三角形的第三边长为
7. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知中, , , 所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的是一个直角三角形),则满足已知条件的三角形的第三边长为 8. 在某次数学探究活动中,小明将一张斜边为4的等腰直角三角形硬纸片剪切成如图所示的四块(其中D,E,F分别为 , , 的中点,G,H分别为 , 的中点),小明将这四块纸片重新组合拼成四边形(相互不重叠,不留空隙),则所能拼成的四边形中周长的最小值为 , 最大值为 .
8. 在某次数学探究活动中,小明将一张斜边为4的等腰直角三角形硬纸片剪切成如图所示的四块(其中D,E,F分别为 , , 的中点,G,H分别为 , 的中点),小明将这四块纸片重新组合拼成四边形(相互不重叠,不留空隙),则所能拼成的四边形中周长的最小值为 , 最大值为 .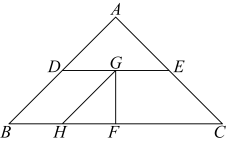 9. 如图, , 矩形的顶点B,C分别是两边上的动点,已知 , , 请完成下列探究:
9. 如图, , 矩形的顶点B,C分别是两边上的动点,已知 , , 请完成下列探究: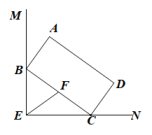 (1)、若点F是的中点,那么;(2)、点D,点E两点之间距离的最大值是 .10. 某班级在探究“将军饮马问题”时抽象出数学模型:
(1)、若点F是的中点,那么;(2)、点D,点E两点之间距离的最大值是 .10. 某班级在探究“将军饮马问题”时抽象出数学模型:直线同旁有两个定点A、B,在直线上存在点 , 使得的值最小.解法:如图1,作点关于直线的对称点 , 连接 , 则与直线的交点即为 , 且的最小值为.请利用上述模型解决下列问题:
 (1)、几何应用:如图2,中,是AB的中点,是BC边上的一动点,则的最小值为;(2)、几何拓展:如图3,中, , 若在AB上取一点 , 则的值最小值是.
(1)、几何应用:如图2,中,是AB的中点,是BC边上的一动点,则的最小值为;(2)、几何拓展:如图3,中, , 若在AB上取一点 , 则的值最小值是.三、实践探究题
-
11. 问题情境:在数学探究活动中,老师给出了如图的图形及下面三个等式:①AB=AC;②DB=DC;③∠BAD=∠CAD.若以其中两个等式作为已知条件,能否得到余下一个等式成立?解决方案:探究△ABD与△ACD全等.

问题解决:
(1)、当选择①②作为已知条件时,△ABD与△ACD全等吗?(填“全等”或“不全等”),理由是(2)、当任意选择两个等式作为已知条件时,请用列表或画树状图的方法求△ABD≌△ACD的概率.12.【问题呈现】
已知,和都是直角三角形, , 连接 , , 探究 , 的位置关系.
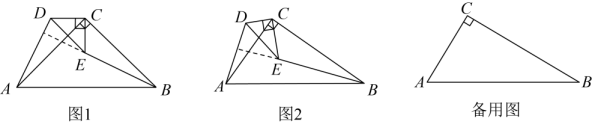 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
13. [知识链接],“化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.在探究平行四边形的性质时,学习小组利用这种思想方法,发现并证明了如下有趣结论,平行四边形两条对角线的平方和等于四边的平方和.请你根据学习小组的思路,完成下列问题: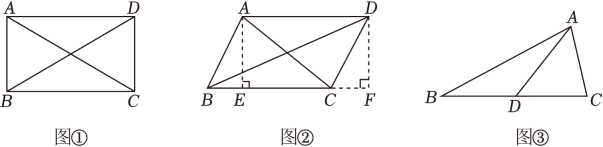 (1)、[问题发现]:如图1,学习小组首先通过对特殊平行四边形——矩形(长方形)的研究发现在矩形ABCD中令AB=a , BC=b , 则可求得AC2+BD2=;(用a、b的式子表示)(2)、[问题探究]:如图2,学习小组通过添加辅助线,尝试将平行四边形转化为矩形,继续对一般平行四边形ABCD进行研究,如图:分别过点A、D作BC边的垂线,请你按照这种思路证明AC2+BD2=2(AB2+BC2);(3)、[问题拓展]:如图3,在△ABC中,AD是BC边上的中线,已知:AD=3,BC=8,(AB-AC)2=10,请你添加合适的辅助线,构造平行四边形进行转化,求AB•AC的值.14. 某数学课外活动小组在学习了勾股定理之后,针对图①中所示的“由直角三角形三边向外侧作多边形,它们的面积S1 , S2 , S3之间的关系问题”进行了以下探究:
(1)、[问题发现]:如图1,学习小组首先通过对特殊平行四边形——矩形(长方形)的研究发现在矩形ABCD中令AB=a , BC=b , 则可求得AC2+BD2=;(用a、b的式子表示)(2)、[问题探究]:如图2,学习小组通过添加辅助线,尝试将平行四边形转化为矩形,继续对一般平行四边形ABCD进行研究,如图:分别过点A、D作BC边的垂线,请你按照这种思路证明AC2+BD2=2(AB2+BC2);(3)、[问题拓展]:如图3,在△ABC中,AD是BC边上的中线,已知:AD=3,BC=8,(AB-AC)2=10,请你添加合适的辅助线,构造平行四边形进行转化,求AB•AC的值.14. 某数学课外活动小组在学习了勾股定理之后,针对图①中所示的“由直角三角形三边向外侧作多边形,它们的面积S1 , S2 , S3之间的关系问题”进行了以下探究: (1)、如图②,在Rt△ABC中,BC为斜边,分别以AB,AC,BC为斜边向外侧作Rt△ABD,Rt△ACE,Rt△BCF,若∠1=∠2=∠3,则面积S1 , S2 , S3之间的关系式为(2)、如图③,在Rt△ABC中,BC为斜边,分别以AB,AC,BC为边向外侧作任意△ABD,△ACE,△BCF,满足∠1=∠2=∠3,∠D=∠E=∠F,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由.15. 阅读材料:若 , 求m、n的值.
(1)、如图②,在Rt△ABC中,BC为斜边,分别以AB,AC,BC为斜边向外侧作Rt△ABD,Rt△ACE,Rt△BCF,若∠1=∠2=∠3,则面积S1 , S2 , S3之间的关系式为(2)、如图③,在Rt△ABC中,BC为斜边,分别以AB,AC,BC为边向外侧作任意△ABD,△ACE,△BCF,满足∠1=∠2=∠3,∠D=∠E=∠F,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由.15. 阅读材料:若 , 求m、n的值.解:∵ , ∴.
∴ , ∴ , , ∴ , .
根据你的观察,探究下面的问题:
(1)、已知 , 求的值.(2)、已知的三边长a、b、c都是正整数,且满足 , 求边c的值.16. [实践与探究]将△ABC(AB>AC)沿AD折叠,使点C刚好落在AB边上的点E处,展开如图,
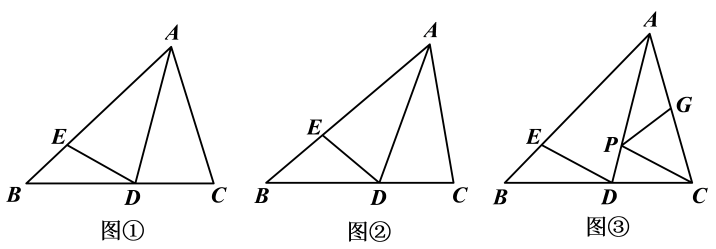 (1)、[操作观察]图①中,AB=8,AC=6.
(1)、[操作观察]图①中,AB=8,AC=6.①BE= .
②若△ACD的面积是9,则△ABD的面积是 .
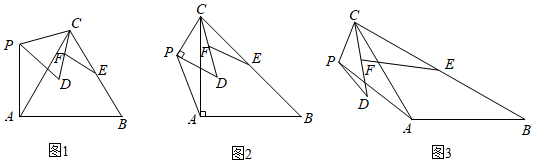
(2)、[理解应用]如图②,若∠C=2∠B,试说明:AB=AC+CD.(3)、[拓展延伸]如图③,若∠BAC=60°,点G为AC的中点,且AG=5.点P是AD上的一个动点,连结PG、PC,直接写出(PG+PC)2的最小值.17. 数学课上,有这样一道探究题.如图,已知中,AB=AC=m,BC=n, , 点P为平面内不与点A、C重合的任意一点,将线段CP绕点P顺时针旋转a,得线段PD,E、F分别是CB、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究的值和的度数与m、n、α的关系,请你参与学习小组的探究过程,并完成以下任务:
 (1)、填空:
(1)、填空:【问题发现】
小明研究了时,如图1,求出了 ▲ , ▲ ;
小红研究了时,如图2,求出了 ▲ , ▲ ;
【类比探究】
他们又共同研究了α=120°时,如图3,也求出了;
【归纳总结】
最后他们终于共同探究得出规律: ▲ (用含m、n的式子表示); ▲ (用含α的式子表示).
(2)、求出时的值和的度数.18. 如图
问题探究:
(1)、如图①,已知线段AB=2,在AB的两侧分别作等边△ABC和Rt△ABD,且∠ADB=90°,CM、DM分别为两个三角形的中线,连接CD,则CD的最大值为;(2)、
如图②,已知△ABC,分别以AB为直角边在△ABC外侧作Rt△ABP,以AC为斜边在△ABC外侧作Rt△ACQ,且∠ABP=∠AQC=90°,∠PAB=∠CAQ=30°,连接PC、BQ,请求出的值;
(3)、如图③,已知边长为a的正方形ABCD,点E是边CB延长线上一动点,连接AE、ED,请问是否存在的最小值?如果存在,求出;如果不存在,请说明理由.19. 问题探究
 (1)、【操作发现】
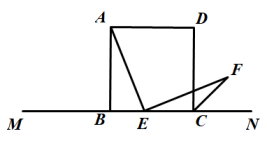
(1)、【操作发现】如图①,在等边△ABC中,点B,C在直线MN上,E为BC边上的一点,连接AE,并把线段AE绕点E顺时针旋转60°得到线段 EF,连接CF,则线段 CF与BE的数量关系是 , 线段CF与直线MN所夹锐角的度数是.
(2)、【类比探究】如图②,在正方形ABCD中,点B,C在直线MN上,E为直线MN上的任意一点,连接AE,并把线段AE绕点E顺时针旋转90°得到线段EF,连接CF,试探究线段BE与CF的数量关系及线段CF与直线MN所夹锐角的度数,并说明理由.
20. 探究问题: (1)、方法感悟:
(1)、方法感悟:如图①,在正方形ABCD中,点E , F分别为DC , BC边上的点,且满足 , 连接EF , 求证 .
感悟解题方法,并完成下列填空:
将绕点A顺时针旋转得到 , 此时AB与AD重合,由旋转可得:
,
,
因此,点G , B , F在同一条直线上.
.
,
.
即 ▲ .
又
▲ .
▲ , 故 .
(2)、方法迁移如图②,将沿斜边翻折得到 , 点E , F分别为DC , BC边上的点,且 . 试猜想DE , BF , EF之间有何数量关系,并证明你的猜想.
(3)、问题拓展:如图③,在四边形ABCD中, , E , F分别为DC , BC上的点,满足 , 试猜想当与满足什么关系时,可使得 , 请直接写出你的猜想(不必说明理由).
21. 【问题情境】在综合实践活动课上,李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动,两块三角板分别记作和 , 设 .
【操作探究】
如图1,先将和的边、重合,再将绕着点A按顺时针方向旋转,旋转角为 , 旋转过程中保持不动,连接 .
 (1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .22. 【问题提出】如图 , 在中, , 点 , 分别为边 , 的中点,将绕点顺时针旋转 , 连接 , , 试探究 , 之间存在怎样的数量关系和位置关系?
(1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .22. 【问题提出】如图 , 在中, , 点 , 分别为边 , 的中点,将绕点顺时针旋转 , 连接 , , 试探究 , 之间存在怎样的数量关系和位置关系? (1)、【特例探究】若 , 将绕点顺时针旋转至图的位置,直线与 , 分别交于点 , 按以下思路完成填空第一个空填推理依据,第二个空填数量关系,第三个空填位置关系:
(1)、【特例探究】若 , 将绕点顺时针旋转至图的位置,直线与 , 分别交于点 , 按以下思路完成填空第一个空填推理依据,第二个空填数量关系,第三个空填位置关系:
, 点 , 分别为边 , 的中点,
.
,
.
≌
▲ , .
又 ,
.
▲ .(2)、【猜想证明】若 , 绕点顺时针旋转至图的位置,直线与 , 分别交于点 , , 猜想与之间的数量关系与位置关系,并就图所示的情况加以证明;
(3)、【拓展运用】若 , , 将绕点顺时针旋转 , 直线与相交于点 , 当以点 , , , 为顶点的四边形是矩形时,请直接写出的长.23. 综合与实践【问题情境】数学活动课上,老师给出了这样一个问题:
如图1,在中, , 射线AD平分 , 将射线AD绕点逆时针旋转 , 得到射线 , 在射线上取点 , 使得 , 连接BE分别交AD,AC于点M,N,连接CE.问:之间的数量关系是什么?线段DM,CN之间的数量关系是什么?

【特例探究】“勤奋”小组的同学们先将问题特殊化,探究过程如下:
甲同学:当时,如图2,通过探究可以发现,都是等腰三角形;
乙同学:可以证明 , 得到;
丙同学:过点做 , 垂足为 , 如图3,则;
丁同学:可以证明 , 则 , …
(1)、根据以上探究过程,得出结论:①之间的数量关系是;
②线段DM,CN之间的数量关系是.
(2)、【类比探究】“智慧”小组的同学们在“勤奋”小组的基础上,进一步探究一般情形,当时,如图1,⑴中的两个结论是否仍然成立?如果成立,请仅就图1的情形进行证明;如果不成立,请说明理由。
(3)、【迁移应用】“创新”小组的同学们改变了条件,当时,如图4,若射线AD是的三等分角线, , 其他条件不变,请直接写出MN的长.
 24. 【探究与证明】成语“以不变应万变”中蕴含着某种数学原理.
24. 【探究与证明】成语“以不变应万变”中蕴含着某种数学原理.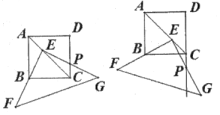
图1 图2
【动手操作】如图1,是正方形的对角线,点E是上的一个动点,过点E和B作等腰直角 , 其中 , , 与射线交于点P.
请完成:
(1)、试判断图1中的和的数量关系;(2)、当点P在线段上时,求证:.(3)、【类比操作】如图2,当点P在线段的延长线上时.是否还成立?请判断并证明你的结论.25. 动手操作:某数学课外活动小组利用图形的旋转探究图形变换中蕴含的数学奥秘.
如图1,△ACB是等腰直角三角形,AC=BC=4,∠ACB=90°,将边AB绕点B顺时针旋转90°得到线段A′B , 连接A′C , 过点A′作A′D⊥CB交CB延长线于点D .
(1)、在图1中:△A′BC的面积为;(2)、如图2,若△ACB为任意直角三角形,∠ACB=90°.将边AB绕点B顺时针旋转90°得到线段A′B , 连接A′C , 过点A′作A′D⊥CB交CB延长线于点D . 猜想三条线段AC、CD、A′D的数量关系,并证明.(3)、如图3,在△ACB中,AB=AC=5,BC=6,将边AB绕点B顺时针旋转90°得到线段A′B , 连接A′C .若点D是△ACB的边BC的高线上的一动点,连接A′D、DB , 则A′D+DB的最小值是 .
26. 综合与探究【问题情境】
数学活动课上,老师带领同学们一起探索旋转的奥秘.老师出示了一个问题:如图1,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上一点 , 连接AD,将△ABD绕着点A按逆时针方向旋转,使AB与AC重合,得到△ACE.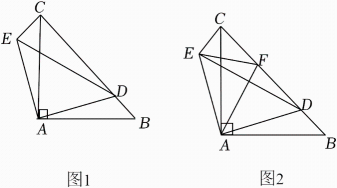 (1)、【操作探究】试判断△ADE的形状,并说明理由;(2)、【深入探究】希望小组受此启发,如图2,在线段CD上取一点F,使得∠DAF=45°,连接EF,发现EF和DF有一定的关系,猜想两者的数量关系,并说明理由;(3)、智慧小组在图2的基础上继续探究,发现CF,FD,DB三条线段也有一定的数量关系,请你直接写出当CF=3,BD=2时DF的长.27. 如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形中, , 过点作射线 , 垂足为 , 点在上.
(1)、【操作探究】试判断△ADE的形状,并说明理由;(2)、【深入探究】希望小组受此启发,如图2,在线段CD上取一点F,使得∠DAF=45°,连接EF,发现EF和DF有一定的关系,猜想两者的数量关系,并说明理由;(3)、智慧小组在图2的基础上继续探究,发现CF,FD,DB三条线段也有一定的数量关系,请你直接写出当CF=3,BD=2时DF的长.27. 如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形中, , 过点作射线 , 垂足为 , 点在上. (1)、【动手操作】
(1)、【动手操作】如图②,若点在线段上,画出射线 , 并将射线绕点逆时针旋转与交于点 , 根据题意在图中画出图形 , 图中的度数为度;
(2)、【问题探究】根据(1)所画图形,探究线段与的数量关系,并说明理由;
(3)、【拓展延伸】如图③,若点在射线上移动,将射线绕点逆时针旋转与交于点 , 探究线段之间的数量关系,并说明理由.
28. 【问题提出】如图1,在中, , 点E,F分别为边AC,BC的中点,将绕点C顺时针旋转 , 连接AE,BF,试探究AE,BF之间存在怎样的数量关系和位置关系?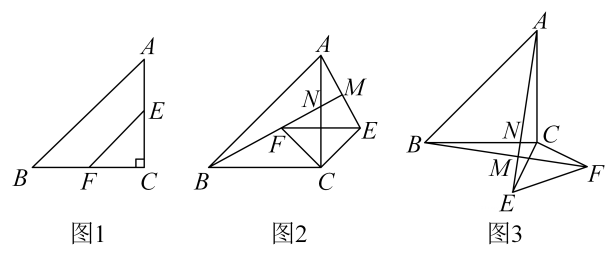 (1)、【特例探究】若 , 将绕点C顺时针旋转至图2的位置,直线BF与AE,AC分别交于点M,N.按以下思路完成填空(第一个空填推理依据,第二个空填数量关系,第三个空填位置关系):
(1)、【特例探究】若 , 将绕点C顺时针旋转至图2的位置,直线BF与AE,AC分别交于点M,N.按以下思路完成填空(第一个空填推理依据,第二个空填数量关系,第三个空填位置关系):∵ , E,F分别为AC,BC的中点,
∴ ,
∵ ,
∴ ,
∴()
∴AEBF, , 又∵ ,
∴ ,
∴AEBM.
(2)、【猜想证明】若 , 绕点C顺时针旋转至图3的位置,直线AE与BF,BC分别交于点M,N,猜想AE与BF之间的数量关系与位置关系,并就图3所示的情况加以证明;(3)、【拓展运用】若 , , 将绕点C顺时针旋转 , 直线AE,BF相交于点M,当以点C,E,M,F为顶点的四边形是矩形时,请直接写出BM的长.29. 胡老师的数学课上,有这样一道探究题.如图,已知 中, ,点P为平面内不与点A、C重合的任意一点,连接 ,将线段 绕点P顺时针旋转 ,得线段 ,连接 点E、F分别为 的中点,设直线 与直线 相交所成的较小角为 ,探究 的值和 的度数与x、y、 的关系.

请您参与学习小组的探究过程,并完成以下任务:
(1)、填空:【问题发现】
小明研究了 时,如图1,求出了 的值和 的度数分别为 , ;
小红研究了 时,如图2,求出了 的值和 的度数分别为 , ;
【类比探究】
他们又共同研究了 时,如图3,也求出了 的值和 的度数;
【归纳总结】
最后他们终于共同探究得出规律: (用含x、y的式子表示); (用含 的式子表示)
(2)、求出 时 的值和 的度数(注:要求写出具体解题过程,否则得零分).30. 数学兴趣小组探究了以下几何图形.如图①,把一个含有角的三角尺放在正方形中,使角的顶点始终与正方形的顶点重合,绕点旋转三角尺时,角的两边 , 始终与正方形的边 , 所在直线分别相交于点 , , 连接 , 可得 .
 (1)、【探究一】
(1)、【探究一】如图②,把绕点C逆时针旋转得到 , 同时得到点在直线上.求证:;
(2)、【探究二】在图②中,连接 , 分别交 , 于点 , . 求证:;
(3)、【探究三】把三角尺旋转到如图③所示位置,直线与三角尺角两边 , 分别交于点 , . 连接交于点 , 求的值.