备考2024年中考数学探究性训练专题18 相交线与平行线
试卷更新日期:2024-03-31 类型:二轮复习
一、选择题
-
1. 小红在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线ln(n=1,2,3,4,5,6,7),其中l1、l2互相平行,l3、l4、I5三条直线交于一点,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个2. 在探究“过直线外一点P作已知直线a的平行线”的活动中,王玲同学通过如下的折纸方式找到了符合要求的直线,在这个过程中她可能用到的推理依据组合是( )

①平角的定义;②邻补角的定义;③角平分线的定义;④同旁内角互补,两直线平行;⑤两直线平行,内错角相等.
A、②④ B、③⑤ C、①②⑤ D、①③④3. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB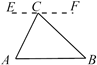 B、过AB上一点D作DE BC,DF AC
B、过AB上一点D作DE BC,DF AC 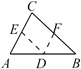 C、延长AC到F,过C作CE AB
C、延长AC到F,过C作CE AB  D、作CD⊥AB于点D
D、作CD⊥AB于点D 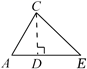 4. 加强对课本习题的探究,对解题有很好的指导作用.如课本第82页有这样一题,如图,AD//BC,BD平分∠ABC,求证:AB=AD.
4. 加强对课本习题的探究,对解题有很好的指导作用.如课本第82页有这样一题,如图,AD//BC,BD平分∠ABC,求证:AB=AD.可将这个题目归纳为:平行加角平分线,得到等腰三角形.请利用这个结论解题:如图,已知△ABC中,I是∠A,∠B,∠C的平分线的交点,AB=6,BC=5,AC=4.平移∠A,使点A与点I重合,两边分别交BC于D,E两点,则△IDE的周长为( )

 A、4 B、5 C、6 D、9
A、4 B、5 C、6 D、9二、填空题
-
5. 在数学活动课上,老师让同学们以“两块直角三角板(一块含角,一块含角)的摆放”为背景开展数学探究活动.某同学将两块三角板按如图所示放置,则下列结论正确的有(直接写序号即可).
①;②若 , 则;③若 , 则;④若 , 则 .
 6. 探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线 ,两点 、 在 上, 于 , 于 ,则 .
6. 探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线 ,两点 、 在 上, 于 , 于 ,则 .如图2,已知直线 , 、 为直线 上的两点, 、 为直线 上的两点.
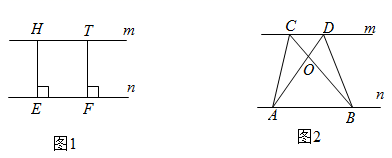 (1)、请写出图中面积相等的各对三角形: .(2)、如果 、 、 为三个定点,点 在 上移动,那么无论 点移动到任何位置总有:与 的面积相等;理由是: .7. 观察下面图形,按要求找角(不含平角),如图①,两条直线交于同一点O,共有对对顶角;如图②,三条直线交于同一点O,共有对对顶角;探究:若有 条直线相交于同一点,则可形成对对顶角.
(1)、请写出图中面积相等的各对三角形: .(2)、如果 、 、 为三个定点,点 在 上移动,那么无论 点移动到任何位置总有:与 的面积相等;理由是: .7. 观察下面图形,按要求找角(不含平角),如图①,两条直线交于同一点O,共有对对顶角;如图②,三条直线交于同一点O,共有对对顶角;探究:若有 条直线相交于同一点,则可形成对对顶角. 8. 在数学探究活动中,“创新”小组进行了如下操作:如图,将矩形纸片ABCD的一角沿过点C的直线折叠,使得点B落在边AD的点H处,再将另一角沿过点C的直线折叠,使得点D落在CH的点Q处,两次折叠的折痕分别为CE、CF。请完成以下探究:
8. 在数学探究活动中,“创新”小组进行了如下操作:如图,将矩形纸片ABCD的一角沿过点C的直线折叠,使得点B落在边AD的点H处,再将另一角沿过点C的直线折叠,使得点D落在CH的点Q处,两次折叠的折痕分别为CE、CF。请完成以下探究: (1)、∠BEC+∠DFC的大小为;(2)、若AB=3,BC=5时, 的值为。9. (问题探究)如图1, ,直线 ,垂足为 ,交 于点 ,点 到直线 的距离为2,点 到 的距离为1, , ,则 的最小值是;(提示:将线段 沿 方向平移1个单位长度即可解决,如图2所示.)
(1)、∠BEC+∠DFC的大小为;(2)、若AB=3,BC=5时, 的值为。9. (问题探究)如图1, ,直线 ,垂足为 ,交 于点 ,点 到直线 的距离为2,点 到 的距离为1, , ,则 的最小值是;(提示:将线段 沿 方向平移1个单位长度即可解决,如图2所示.)(关联运用)如图3,在等腰 和等腰 中, , 在直线 上, ,连接 、 ,则 的最小值是.

三、作图题
-
10. 小冬阅读了教材中“借助三角尺画角”的探究活动(如图1、图2的实物图所示),他在老师指导下画出了图1所对应的几何图形,并标注了所使用三角尺的相应角度(如图3),他发现用一副三角尺还能画出其他特殊角.

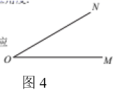
请你借助三角尺完成以下画图,并标注所使用三角尺的相应角度.
(1)、画出图2对应的几何图形;(2)、设计用一副三角尺画出角的画图方案,并画出相应的几何图形;(3)、如图4,已知 , 画∠MON的角平分线OP.四、实践探究题
-
11. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,求DE的长
 12. 小明在一组平行线中作角,探究两边与平行线形成的锐角的数量关系.
12. 小明在一组平行线中作角,探究两边与平行线形成的锐角的数量关系. (1)、如图1,他先作出 , 且点在一条直线上,当时, . 点在两条平行线之间,如图2,请用等式表示与的数量关系并证明.(2)、在图3中, , 点在两条平行线之间,记与图中一条直线形成的锐角为 , 若小明作射线 , 使得 , 记与图中另一条直线形成的锐角为 , 请用等式表示与之间的数量关系.13. 综合与探究
(1)、如图1,他先作出 , 且点在一条直线上,当时, . 点在两条平行线之间,如图2,请用等式表示与的数量关系并证明.(2)、在图3中, , 点在两条平行线之间,记与图中一条直线形成的锐角为 , 若小明作射线 , 使得 , 记与图中另一条直线形成的锐角为 , 请用等式表示与之间的数量关系.13. 综合与探究
【问题】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB,∠EDF=90,点D在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系。
【探究发现】
(1)、如图2,某数学学习小组运用“从特殊到一般”的数学思想,发现当点D移动到使点P与点C重合时,很容易就可以得到DP=DB,请写出证明过程;(2)、如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,另一个学习小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程。(3)、若点P是CA延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立。14. 如图,已知格线相互平行,小明在格线中作∠AOB、∠CPD、∠EOF,探究角的两边与格线形成的锐角所满足的数量关系. (1)、如图1,∠AOB=60°,点O在一条格线上,当∠1=20°时,求∠2的度数;(2)、如图2,∠CPD=60°,点Р在两条格线之间,用等式表示∠3与∠4的数量关系,并证明;(3)、如图3,∠EOF=60°,小明在图3中作射线QG,使得∠GOF=45°.记QG与图中一条格线形成的锐角为α,QE与图中另一条格线形成的锐角为β,探究α与β的数量关系,并用等式表示α与β的数量关系.15. 综合与探究
(1)、如图1,∠AOB=60°,点O在一条格线上,当∠1=20°时,求∠2的度数;(2)、如图2,∠CPD=60°,点Р在两条格线之间,用等式表示∠3与∠4的数量关系,并证明;(3)、如图3,∠EOF=60°,小明在图3中作射线QG,使得∠GOF=45°.记QG与图中一条格线形成的锐角为α,QE与图中另一条格线形成的锐角为β,探究α与β的数量关系,并用等式表示α与β的数量关系.15. 综合与探究 (1)、如图1, , , 则与之间的数量关系为;如图2, , , 则与之间的数量关系为 .(2)、在图3中, , , , , 求的度数.(3)、在图4中, , , , 平分 , 试探究、与之间的数量关系.16. 直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
(1)、如图1, , , 则与之间的数量关系为;如图2, , , 则与之间的数量关系为 .(2)、在图3中, , , , , 求的度数.(3)、在图4中, , , , 平分 , 试探究、与之间的数量关系.16. 直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!【问题探究】

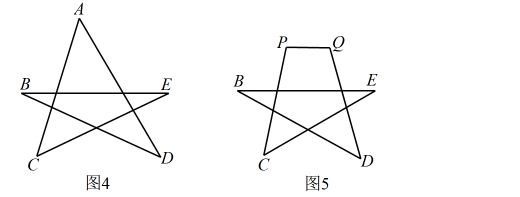 (1)、①如图1,若 , 点P在内部, , 则;
(1)、①如图1,若 , 点P在内部, , 则;②如图2,若 , 将点P在外部,求之间数量关系(不需证明);
③如图3,写出之间的数量关系:(不需证明).
(2)、如图4,五角星 , 请直接写出 .(3)、如图5,将五角星去掉一个角后,是多少?请证明你的结论.17. 在学习了图形的旋转知识后,某数学兴趣小组对教材中有关图形旋转的问题进行了进一步探究. (1)、问题梳理:
(1)、问题梳理:问题呈现:如图1,点D在等边三角形ABC的边BC上,过点C作AB的平行线l,在l上取CE=BD,连结AE,则在图1中会产生一对旋转图形.请结合问题中的条件,证明:△ABD≌△ACE.
(2)、初步尝试:如图2,在△ABC中,AB=AC,点D在边BC上,且BD<DC,将△ABD沿某条直线翻折,使得AB与AC重合,点D与BC边上的点F重合,再将△ACF沿AC所在直线翻折,得到△ACE,则在图2中会产生一对旋转图形.若∠BAC=30°,AD=6,连结DE,求△ADE的面积.
(3)、深入探究:如图3,在△ABC中,AC=6,D是边BC上的任意一点,连结AD,将线段AD绕点A按逆时针方向旋转75°,得到线段AE,连结CE,求线段CE长度的最小值.
18.
【问题提出】小颖同学在学习中自主探究以下问题,请你解答她提出的问题:
(1)、如图所示,已知 , 点为 , 之间一点,连接 , , 得到请猜想与、之间的数量关系,并证明;猜想: ▲ ;
证明:
(2)、如图所示,已知 , 点为 , 之间一点,和的平分线相交于点 , 若 , 求的度数;(3)、【类比迁移】小颖结合角平分线的知识将问题进行深入探究,如图所示,已知: , 点的位置移到上方,点在延长线上,且平分与的平分线相交于点 , 请直接写出与之间的数量关系;(4)、【变式挑战】小颖在本次探究的最后将条件去掉,提出了以下问题:已知与不平行,如图 , 点在上,点在上,连接 , 且同时平分和 , 请直接写出 , , 之间的数量关系 .
19. 小明完成作业后在家复习,他看到七下课本第12页例4,感到这个结论十分有趣,便尝试探究起来. (1)、【基础巩固】
(1)、【基础巩固】与例4条件和结论互换,改成了:“如图1,AP 平分∠BAC,CP平分∠ACD,AB∥CD,则∠1+∠2=90°,”小明认为这个结论正确,你赞同他的想法吗? 请说明理由.
(2)、【尝试探究】小明发现:若将其中一条角平分线改成AC的垂线,则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究:
如图2,AB∥CD,AP平分∠BAC,CP⊥AC,∠1是AP与AB的夹角,∠2 是CP与CD的夹角.
①若∠2=22°,求∠1的度数.
②试说明:2∠1-∠2=90°.
(3)、【拓展提高】如图3,若AB∥CD,AP⊥AC,CP平分∠ACD,请直接写出∠1与∠2的数量关系.
20. 综合与探究数学活动课上,老师以“一个含的直角三角板和两条平行线”为背景展开探究活动,

如图1,已知直线 , 直角三角板中, , .
(1)、如图1,若 , 则;(直接写出答案)(2)、“启航”小组在图1的基础上继续展开探究:如图 , 调整三角板的位置,当三角板的直角顶点在直线上,直线与 , 相交时,他们得出的结论是: , 你认为启航小组的结论是否正确,请说明理由;(3)、如图 , 受到“启航”小组的启发,“睿智”小组提出的问题是:在图的基础上,继续调整三角板的位置,当点不在直线上,直线与 , 相交时,与有怎样的数量关系?请你用平行线的知识说明理由.21. 某数学学习小组学习完四边形后进行了如下探究,已知四边形为矩形,请你帮助他们解决下列问题: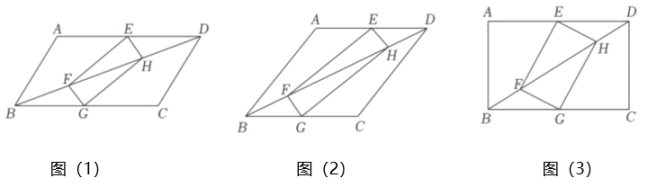 (1)、【初步尝试】:他们将矩形的顶点E、G分别在如图(1)所示的的边、上,顶点F、H恰好落在的对角线上,求证::(2)、【深入探究】:如图2,若为菱形, , 若 , 求的值;(3)、【拓展延伸】:如图(3),若为矩形,;且 , 请直接写出此时的值是(用含有m , n的代数式表示).22. 数学兴趣小组围绕“三角形的内角和是”,进行了一系列探究,过程如下:
(1)、【初步尝试】:他们将矩形的顶点E、G分别在如图(1)所示的的边、上,顶点F、H恰好落在的对角线上,求证::(2)、【深入探究】:如图2,若为菱形, , 若 , 求的值;(3)、【拓展延伸】:如图(3),若为矩形,;且 , 请直接写出此时的值是(用含有m , n的代数式表示).22. 数学兴趣小组围绕“三角形的内角和是”,进行了一系列探究,过程如下: (1)、【论证】如图 , 延长至点 , 过点作 , 就可以说明成立,即:三角形的内角和为请完成上述说理过程.(2)、【应用】如图 , 在中,的平分线与的角平分线交于点 , 过点作 , 在射线上,且 , 的延长线与的延长线交于点 .
(1)、【论证】如图 , 延长至点 , 过点作 , 就可以说明成立,即:三角形的内角和为请完成上述说理过程.(2)、【应用】如图 , 在中,的平分线与的角平分线交于点 , 过点作 , 在射线上,且 , 的延长线与的延长线交于点 .求的度数;
设 , 请用的代数式表示 .
(3)、【拓展】如图 , 在中, , , 过点作 , 直线与相交于点右侧的点 , 绕点以每秒的速度顺时针方向旋转,同时绕点以每秒的速度顺时针方向旋转,与重合时再绕着点以原速度逆时针方向旋转,当旋转一周时,运动全部停止设运动时间为秒,在旋转过程中,是否某一时刻,使得与的一边平行?若存在,求的值;若不存在,请说明理由.23. 综合探究如图,在中, , 是的平分线,是边上的高,垂足为 , 设 .
 (1)、探究与发现
(1)、探究与发现① 如图1,若 , 则的度数为 ▲ , 的度数为 ▲ ;
② 如图2,若 , 则的度数为 ▲ ;
③ 试探究与的数量关系,并说明理由.
(2)、 拓展与思考如图3,的平分线交于点 . 当时,求的度数.
24. 某托管服务数学兴趣小组针对如下问题进行探究,在等边中, , 点在射线上运动,连接 , 以为一边在右侧作等边 . (1)、【问题发现】如图 , 当点在线段上运动时不与点重合 , 连接则线段与的数量关系是 ;直线与的位置关系是 ;(2)、【拓展延伸】如图 , 当点在线段的延长线上运动时,直线 , 相交于点 , 请探究的面积与的面积之间的数量关系;(3)、【问题解决】当点在射线上运动时点不与点 , 重合 , 直线 , 相交于点 , 若的面积是 , 请求出线段的长.25. 【问题背景】
(1)、【问题发现】如图 , 当点在线段上运动时不与点重合 , 连接则线段与的数量关系是 ;直线与的位置关系是 ;(2)、【拓展延伸】如图 , 当点在线段的延长线上运动时,直线 , 相交于点 , 请探究的面积与的面积之间的数量关系;(3)、【问题解决】当点在射线上运动时点不与点 , 重合 , 直线 , 相交于点 , 若的面积是 , 请求出线段的长.25. 【问题背景】如图, . 连接 , 点E,F在上,且 , 连接 , 且 .
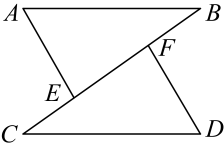
【问题探究】
(1)、试说明::(2)、若 ,①试判断的形状,并说明理由:
②若 , 求的度数.
26. 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形和等腰直角三角形 , 按如图1的方式摆放, . 该数学兴趣小组进行如下探究,请你帮忙解答:(1)、【初步探究】如图1,试探究与的位置关系,并说明理由; (2)、【深入探究】如图2,当、、三点共线时,请探究此位置时线段、、之间的数量关系,并说明理由;
(2)、【深入探究】如图2,当、、三点共线时,请探究此位置时线段、、之间的数量关系,并说明理由; (3)、【拓展延伸】如图3,当、、三点不共线时,连接 , 延长交于点 , 连接 , 请猜想此位置时线段、、之间的数量关系: .
(3)、【拓展延伸】如图3,当、、三点不共线时,连接 , 延长交于点 , 连接 , 请猜想此位置时线段、、之间的数量关系: .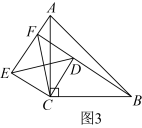 27. 学习完平行线的知识后,甲,乙,丙三位同学利用两个三角形进行探究活动,分别得到以下图形.已知中, . 请根据他们的叙述条件完成题目.
27. 学习完平行线的知识后,甲,乙,丙三位同学利用两个三角形进行探究活动,分别得到以下图形.已知中, . 请根据他们的叙述条件完成题目. (1)、若为等腰直角三角形,且;
(1)、若为等腰直角三角形,且;①甲同学:如图1,和的直角边在同一直线上,点E和点C互相重合,斜边与相交于点P,那么∠APF= ▲ 度;
②乙同学:如图2,和直角顶点C,D互相重合于点P,斜边与斜边互相平行,求的度数,并写出解答过程;
(2)、若为等腰三角形,已知 .丙同学:如图3,若直角顶点D恰好与底边的中点重合,的斜边经过的顶点C,若 , 设 , 请用含x的式子表示的度数,并写出解答过程.
28. 问题情境:在数学探究活动课上,老师让同学们以“两条平行线 , 和一块含30°角的直角三角板”为主题开展数学探究活动. (1)、探究发现:如图-1,小明把三角板的60°角的顶点放在上,若 , 则°;(2)、如图-2,小亮把三角板的两个锐角的顶点 , 分别放在和上,请你探索并说明与之间的数量关系;(3)、如图-3,小颖把三角板的直角顶点放在上,30°角的顶点放在上.若 , 直接写出的度数(用含的代数式表示);(4)、拓展延伸:若将如图-3所示的三角形绕直角顶点顺时针旋转一周,每秒转动10°,直接写出当时,三角形旋转所用的时间(用含的代数式表示).29. 数学探究活动中,阿青同学为了验证:长条纸片上下边沿与是否平行,把纸片沿着折叠(如图1),并用量角器测出的度数;
(1)、探究发现:如图-1,小明把三角板的60°角的顶点放在上,若 , 则°;(2)、如图-2,小亮把三角板的两个锐角的顶点 , 分别放在和上,请你探索并说明与之间的数量关系;(3)、如图-3,小颖把三角板的直角顶点放在上,30°角的顶点放在上.若 , 直接写出的度数(用含的代数式表示);(4)、拓展延伸:若将如图-3所示的三角形绕直角顶点顺时针旋转一周,每秒转动10°,直接写出当时,三角形旋转所用的时间(用含的代数式表示).29. 数学探究活动中,阿青同学为了验证:长条纸片上下边沿与是否平行,把纸片沿着折叠(如图1),并用量角器测出的度数;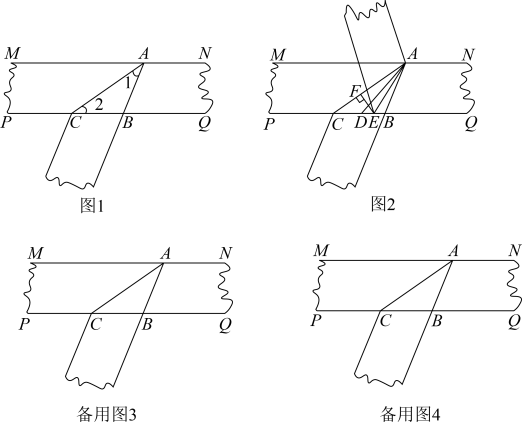 (1)、若 , 则.你认为阿青同学的做法正确吗?㳻说明理由;(2)、在(1)的条件下,阿青同学在纸条下上取点(如图2),连结并沿着折叠纸片使得与重合,过作于点 , 设 , .
(1)、若 , 则.你认为阿青同学的做法正确吗?㳻说明理由;(2)、在(1)的条件下,阿青同学在纸条下上取点(如图2),连结并沿着折叠纸片使得与重合,过作于点 , 设 , .①当点在点之间时,若 , 求的度数;
②当点在上的运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明.(选其中一种情况证明)
-