辽宁省沈阳市2023-2024学年九年数下学期开学数学初限时作业训练

试卷更新日期：2024-03-30 类型：开学考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 下面计算正确的是（）

A、a²•a³＝a⁶ B、（-2a²）³＝-8a⁶ C、a⁹÷a³＝a³ D、2a²+a²＝3a⁴

查看试题解析
2. 下列变形正确的是（）

A、如果x＝y，那么x+5＝y-5 B、如果x＝y，那么-2x＝-2y C、如果x＝y，那么 $\frac{x}{c} = \frac{y}{c}$ D、如果 $\frac{1}{2} x = 6$ ，那么x＝3

查看试题解析
3. 在平面直角坐标系中，点（0，-3）在（）

A、x轴的正半轴 B、y轴的负半轴 C、x轴的负半轴 D、y轴的正半轴

查看试题解析
4. 抛物线y＝x²-4x+9的顶点坐标是（）

A、（-2，5） B、（2，5） C、（2，-5） D、（-2，-5）

查看试题解析
5. 在反比例函数 $y = \frac{k^{2} + 1}{x}$ （ $k$ 为常数）上有三点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ ，若 $x_{1} < 0 < x_{2} < x_{3}$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
6. 正八边形中，每个内角与每个外角的度数之比为（）

A、1：3 B、1：2 C、2：1 D、3：1

查看试题解析
7. 下列表格是某公司员工情况表，你在了解这家公司的员工的平均工资时，你最应该关注的数据是（）
职位
普工
文员
经理
董事长
人数
3
10
2
1
工资（元）
1200
1500
1600
8000

A、平均数 B、众数与中位数 C、方差 D、最小数

查看试题解析
8. 古希腊数学家埃拉托色尼是第一个测算地球周长的人，他在当时的城市塞恩（图中的点A）竖立的杆子在某个时刻没有影子，而此时在500英里以外的亚历山大（图中的点B）竖立杆子的影子却偏离垂直方向约 $7 ° (∠ α \approx 7 °)$ ，由此他得出 $∠ α = ∠ β$ ，那么 $∠ β$ 的度数也就是 $360 °$ 的 $\frac{1}{50}$ ，所以从亚历山大到塞恩的距离也就等于地球周长的 $\frac{1}{50}$ ．其中“ $∠ α = ∠ β$ ”所依据的数学定理是（）

A、两直线平行，内错角相等 B、两直线平行，同位角相等 C、两直线平行，同旁内角互补 D、内错角相等，两直线平行

查看试题解析
9. 如图， $△ A B C$ 外接圆的圆心坐标是（）

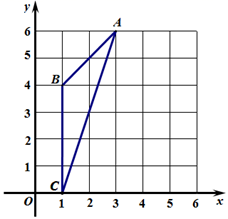A、(5，2) B、(2，3) C、(1，4） D、(0，0)

查看试题解析
10. 如图，矩形ABCD中，AB＝6，BC＝8．将矩形ABCD绕点A逆时针旋转90°到矩形AGFE的位置，H是对角线AF的中点，则线段DH的长为（）

A、 $\sqrt{41}$ B、 $2 \sqrt{10}$ C、 $\sqrt{21}$ D、 $2 \sqrt{5}$

查看试题解析

二、填空题（共5小题，每小题3分，共15分）

11. 面对新冠肺炎疫情对经济运行的冲击，中国人民银行营业管理部（中国人民银行总行在京派驻机构）与相关部门多方动员，截至2020年4月2日，已发放优惠利率贷款573笔，金额280亿元．将280亿元用科学记数法表示应为元．

查看试题解析
12. |-2021|＝．

查看试题解析
13. 掷一枚质地均匀的硬币，前 $8$ 次都是正面朝上，则掷第 $9$ 次正面朝上的概率是．

查看试题解析
14. 如图，在平面直角坐标系中，直线 $y = \frac{\sqrt{3}}{3} x + 2$ 与x轴交于点A，与y轴交于点B，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线 $y = \frac{k}{x} (k \neq 0)$ 上，则k的值为．

查看试题解析
15. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $A B = 16$ ，点 $P$ 是 $A C$ 边上的一个动点，将线段 $B P$ 绕点 $B$ 顺时针旋转60°得到线段 $B Q$ ，连接 $C Q$ ，则在点 $P$ 运动过程中，线段 $C Q$ 的最小值为.

查看试题解析

三、解答题（共8小题，共75分）

16.

(1)、解不等式4（x-1）+3≤2x+5，并把它的解集在数轴上表示出来．

(2)、计算： ${(\frac{1}{2})}^{- 2} - {(π - 2020)}^{0} - | \sqrt{12} - 3 | + 2 c o s 30 °$ ．

查看试题解析
17. 某校为了解学生对偶像崇拜的情况，从本校学生中随机抽取60名学生，进行问卷调查，并将调查结果收集整理如下：
调查问卷
2023年6月
你崇拜的偶像是（）（单选）
A．娱乐明星 B．英雄人物
C．科学家 D．其他
收集数据：
A、D、C、C、A、D、B、B、A、C、D、B、D、A、C、A、C、C、C、C、D、C、A、D、B、B、C、A、A、C、B、B、C、A、C、B、C、C、B、C、A、C、C、A、C、A、C、A、A、C、A、C、C、C、B、B、D、B、D、D．
整理数据：
崇拜偶像人数统计表
偶像类型
划记
人数
百分比
A．娱乐明星
正正正
15
25%
B．英雄人物
正正下

C．科学家
正正正正正
24
40%
D．其他

9
15%
描述数据：
请根据所统计信息，解答下列问题：

(1)、请补全统计表和条形统计图并填空n＝；

(2)、若该校共有1600名学生，其中崇拜英雄人物和科学家的共约多少人？

(3)、请你针对中学生崇拜偶像问题．提出积极的合理化的建议．

查看试题解析
18. 欧城物业为美化小区，要对面积为9600平方米的区域进行绿化，计划安排甲、乙两个园林队完成，已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍，并且甲、乙两园林队独立完成面积为800平方米区域的绿化时，甲园林队比乙园林队少用2天．求甲、乙两园林队每天能完成绿化的面积分别是多少平方米．

查看试题解析
19. 如图，一条公路的两侧互相平行，某课外兴趣小组在公路一侧AE的点A处测得公路对面的点C与AE的夹角∠CAE=30°，沿着AE方向前进15米到点B处测得∠CBE=45°，求公路的宽度.（结果精确到0.1米，参考数据： $\sqrt{3}$ ≈1.73）

查看试题解析
20. 某电脑销售公司在5月份售出甲、乙、丙三种型号的电脑若干台，每种型号的电脑不少于10台．这个月的支出包括以下三项：这批产品的进货总成本850000元，人员工资和其他支出．这三种电脑的进价和售价如表所示，人员工资y₁（元）与总销售量x（台）的关系式为y₁＝400x+12000，其他支出y₂（元）与总销售量x（台）的函数图象如图所示．
型号
甲
乙
丙
进价（元/台）
4500
6000
5500
售价（元/台）
6000
8000
6500

(1)、求其他支出y₂（元）与总销售量x（台）的函数关系式；

(2)、如果该公司5月份的人员工资和其他支出共90000元，求该公司5月份共售出甲、乙、丙三种型号的电脑多少台？

(3)、在（2）的条件下，求该公司5月份销售甲、乙、丙三种产品总利润W的最大值，并求出此时三种电脑各销售了多少台？（利润＝售价-进价-人员工资-其他支出）

查看试题解析
21. 如图，△ABC内接于⊙O，⊙O的直径AD与弦BC相交于点E，BE＝EC，过点D的切线交AC的延长线于点F．

(1)、求证：BC∥DF；

(2)、若sin∠BAD= $\frac{\sqrt{5}}{5}$ ， AB＝ $4 \sqrt{5}$ ，求AF的长．

查看试题解析
22. 如图，抛物线y＝ax²+bx+c过点A（-1，0），B（3，0），C（0，3）．

(1)、求抛物线的解析式；

(2)、设点P是直线BC上方抛物线上一点，求出△PBC的最大面积及此时点P的坐标；

(3)、若点M是抛物线对称轴上一动点，点N为坐标平面内一点，是否存在以BC为边，点B、C、M、N为顶点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析
23. 小明在学习过程中，对教材的一个习题做如下探究：

(1)、【习题回顾】：如图，在等边三角形ABC的AC、BC边上各取一点P，Q使AP＝CQ，AQ，BP相交于点O，求∠BOQ的度数．请你解答该习题．

(2)、【拓展延伸】：如图1，在等腰Rt△ABC的AC，BC边上各取一点P，Q，使AP＝CQ，BP平分∠ABC， AQ= $\sqrt{2}$ ， ∠BAC＝90°，求BP的长．小明的思路：过点A作AG∥BC交BP延长线于点G，证明△AQC≌△GPA，

(3)、如图2，在Rt△ABC的AC、BC边上各取一点P、Q，使CQ＝2AP，BP平分∠ABC， $\frac{A B}{A C} = \frac{1}{2}$ ， ∠BAC＝90°，求AQ，BP的数量关系，请你解答小明提出的问题．

查看试题解析

职位	普工	文员	经理	董事长
人数	3	10	2	1
工资（元）	1200	1500	1600	8000

偶像类型	划记	人数	百分比
A．娱乐明星	正正正	15	25%
B．英雄人物	正正下
C．科学家	正正正正正	24	40%
D．其他		9	15%

型号	甲	乙	丙
进价（元/台）	4500	6000	5500
售价（元/台）	6000	8000	6500