广西南宁市青秀区第十四中2023-2024学年九年级下学期数学开学考试卷

试卷更新日期：2024-03-30 类型：开学考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的、用2B铅笔把答题卡上对应题目的答案标号涂黑．）

1. 中国是最早采用正负数表示相反意义的量并进行负数运算的国家，若收入300元记作+300元．则支出125元记作（）

A、+125元 B、-125元 C、-300元 D、+300元

查看试题解析
2. 中华文明，源远流长：中华汉字，离意深广．下列四个选项中，是暂对称图形的为（）

A、 B、 C、 D、

查看试题解析
3. 据拫道，2024年元旦假期国内旅游出游135000000人次．数字135000000用科学记数法表示是（）

A、 $13.5 \times 1 0^{7}$ B、 $1.35 \times 1 0^{9}$ C、 $0.135 \times 1 0^{9}$ D、 $1.35 \times 1 0^{9}$

查看试题解析
4. 下列几何体中，三视图的三个视图完全相同的几何体是（）

A、 B、 C、 D、

查看试题解析
5. 如图，数轴上表示的是一个不等式组的解集，则这个不等式组的解集是（）

A、 $x ⩾ - 1$ B、 $x < 2$ C、 $- 1 ⩽ x ⩽ 2$ D、 $- 1 ⩽ x < 2$

查看试题解析
6. 某学校开设了社团课程，小明从感兴起的“茶艺”、“烘溶”、“篮球”、“舞蹈”4门课程中随机选择一门学习，每门课程被选中的可能性相等．小明恰好选中“烘焙”的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
7. 如图， $a / / b, ∠ 1 = 12 0^{°}$ ，则 $∠ 2$ 的度数是（）

A、 $6 0^{°}$ B、 $8 0^{°}$ C、 $4 0^{°}$ D、 $12 0^{°}$

查看试题解析
8. 下列运算正确的是（）

A、 $m^{2} - m = m$ B、 $2 m^{2} \cdot 5 m^{4} = 10 m^{6}$ C、 $4 m^{2} + 3 m = 7 m^{3}$ D、 ${(2 m^{2})}^{4} = 16 m^{6}$

查看试题解析
9. 正比例函数 $y_{1} = k_{1} x (k_{1} > 0)$ 的图像与反比例函数 $y_{2} = \frac{2}{x}$ 的图象相交于A、B两点，其中 $A$ 点的模坐标为2，当 $y_{1} < y$ ，时， $x$ 的取值范围是（）

A、 $x < - 2$ 或 $x > 2$ B、 $x < - 2$ 或 $0 < x < 2$ C、 $- 2 < x < 0$ 或 $0 < x < 2$ D、 $- 2 < x < 0$ 或 $x > 2$

查看试题解析
10. 《九章算术》是中国古代重要的数学著作，其中有这样一道题；“今有醇酒一斗，直钱五十；行酒一斗，直钱一十．今将钱三十，得酒二斗，问醇、行酒各得几何?”译文：今有醇酒（优质酒)1斗，价格50钱；行酒（勾兑酒)1斗，价格10钱．现有30钱，买2斗酒，问能买醇酒、行酒各多少斗？设能买醇酒x斗。行酒y斗，可列二元一次方程组为（）

A、 ${\begin{array}{l} x + y = 2 \\ 10 x + 50 y = 30 \end{array}$ B、 ${\begin{array}{l} x + y = 2 \\ 30 x + 10 y = 50 \end{array}$ C、 ${\begin{array}{l} x + y = 2 \\ 10 x + 30 y = 50 \end{array}$ D、 ${\begin{array}{l} x + y = 2 \\ 50 x + 10 y = 30 \end{array}$

查看试题解析
11. 如图，已知 $△ A B C$ 和 $△ A^{^{'}} B^{^{'}} C^{^{'}}$ 是以点 $O$ 为位似中心的位似图形，点 $A$ 在线叹 $O A^{^{'}}$ 上． $△ A B C$ 周长为4，若 $A A^{^{'}} = 2 O A$ ，财 $△ A^{^{'}} B^{^{'}} C^{^{'}^{'}}$ 的周长为（）

A、12 B、10 C、8 D、6

查看试题解析
12. 如图，平面直角坐标系xOy中，抛物线 $y = a x + b x + c$ 与直线 $y = k x$ 交于 $M$ ， $N$ 两点，则二次函数 $y = a x^{2} + (b - k) x + c$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析

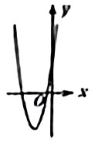
二、填空题（本大题共6小题，每小题2分，共12分．）

13. 若分式 $\frac{2}{x - 3}$ 有道义，则头数 $x$ 的叹值范围是.

查看试题解析
14. 分解因式： $x^{2} - y^{2} =$

查看试题解析
15. 小红应聘小记者，进行了两项测试，测试成绩分别是：采访写作90分、计算机输入70分，若将采访写作和计算机输入两项成绩按3：2的比例来计算平均成绩，则小红的平均成绩是分.

查看试题解析
16. 如图，我校数学兴趣小组在 $A$ 处用仪器测得一宣传气球顶部 $E$ 处的仰角为 $26.56 6^{°}$ ，仪器与气球的水平距离BC为30米，且距地面高度AB为2.5米，则气球顶部都离地面的高度EC是米（结果精确到0.1米， $s i n 26.56 6^{°} \approx 0.4472, c o s 26.56 6^{°} \approx 0.8944, t a n 26.56 6^{°} \approx 0.5000$ ）.

查看试题解析
17. 如图，直径AB=6的半圆，绕B点逆时针旋转30°，此时点A到了点A'，则图中阴影部分的面积是.

查看试题解析
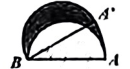18. 如图，在□ABCD中， $A B = 4, A D = 6$ ，点 $E$ 在AD的延长线上，且 $D E = 2$ ，过点 $E$ 作直线 $l$ 分别交边CD，AB于点M，N．若直线 $l$ 将□ABCD的面积平分，则线段CM的长为.

查看试题解析

三、解答题(本大题共8小题，共72分.解答应写出文字说明、证明过程或演算步骤.)

19. 计算： $(- 4 + 2) \times 5 + (- 3)^{3} \div 9$ .

查看试题解析
20. 解方程： $x^{2} - 3 x + 2 = 0$ .

查看试题解析
21. 下面是小明同学要借助无刻度的直尺和圆规作图，来证明三角形内角和等于180°这一命题，请你帮他补充完整.
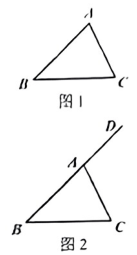
命题：三角形的三个内角的和等于 $18 0^{°}$ ．
已知：如图1． $△ A B C$ ．
求证： $∠ A + ∠ B + ∠ C = 18 0^{°}$ ．
证明：如图2．延长BA到 $D$ ，以AC为边，在其右侧尺规作 $∠ C A E = ∠ C$ ，
∵∠CAE=∠C.
∴……

查看试题解析
22. 为落实立德树人的根本任务，着力培养学生的核心素养．某中学选取了A“广西药用植物园”，B.“广西民族傅物馆”，C.“广西科技馆”，D.“南宁园博园”四个研学基地进行研学．为了解学生对以上研学基地的喜爱情况，随机抽取部分学生进行调查统计(每名学生只能选择一个研学基地)，并将调查结果绘制成了两幅不完整的统计图(如图所示).
请根据统计图中的信息解答下列问题：

(1)、请你求出本次调查抽取学生的总人数，并将上面的条形统计图补充完整；

(2)、若该校共有650名学生，请你估计选择研学基地A的学生人数；

(3)、学校想从选择研学基地B的学生中选取两名学生了解他们对研学活动的看法，已知选择研学基地B的学生中恰有一名女生，请用列表法或画树状图的方法求出所选2人都是男生的概率.

查看试题解析
23. 如图，AB是 $⊙ O$ 的直径，点C，D是 $⊙ O$ 上的点，AC分别与BD，OD相交于点E，P．且 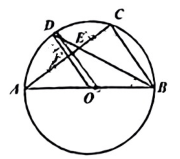$A F = F C$ ．

(1)、求证： $O D / / B C$ ：

(2)、若 $D F = 2, A C = 8$ ，求 $⊙ O$ 的直径．

查看试题解析
24. 在平面直角坐标系中．二次函数图象的表达式为 $y = a x^{z} + (a + 1) x + b$ ，其中 $a - b = - 2$ ．

(1)、若此函数图象过点 $(1, 6)$ ，求这个二次函数的表达式．

(2)、若 $(x_{1}, y_{1})$ 和 $(x_{2}, y_{2})$ 为此二次函数图枲上两个不同点．当 $x_{1} + x_{2} = 4$ 时， $y_{1} = y_{2}$ ，求 $a$ 的值．

(3)、已知 $a > 0$ ，若点（1． $t$ ）在此二次函数图象上，且当 $x ⩽ - 2$ 时 $y$ 随 $x$ 的增大而减小，求 $t$ 的范围．

查看试题解析
25. 综合与实践
【发现问题】“速叠杯”是深受学生喜爱的一项运动，杯子的叠放方式如图1所示：每层都是杯口朝下排成一行，自下向上逐层递减一个杯子，直至顶层只有一个杯子，爱思考的小丽发现叠放所需杯子的总数随着第一层（最底层）杯子的个数变化而变化.
【提出问题】叠放所需杯子的总数y与第一层杯子的个数x之间有怎样的函数关系?
【分析问题】小丽结合实际操作和计算得到下表所示的数据：
第一层杯子的个数x
1
2
3
4
5
杯子的总数y
1
3
6
10
15
…
然后在平面直角坐标系中，描出上面表格中各对数值所对应的点，得到图2、小丽根据图2中点的分布情况，猜想其图象是二次函数图象的一部分；为了验证自己的猜想，小丽从“形”的角度出发．将要计算总数的杯子用黑色圆表示（如图3)，再借助“补”的思想，补充相同数量的白色圆，使每层圆的数量相同，进而求出y与x的关系式.

(1)、【解决问题】
直接写出 $y$ 与 $x$ 的关系式；

(2)、现有28个杯子，按【发现问题】中的方式叠放，求第一层怀了的个数；

(3)、杯子的侧面展开图如图4所示，ND，MA分别为上、下底面圆的半径， $N D / / M A . \hat{A B}$ 所对的圆心角 $∠ A O B = 12 0^{°} . O A = 18 c m, O D = 8 c m$ ．将这样足够数量的杯子按【发现问题】中的方式叠放，但受桌面长度限制，第一层提放杯子的总长度不超过 $108 c m$ ，求杯子叠放达到的最大高度和此时杯子的总数

查看试题解析
26.
【问题情境】如图，在 $△ A B C$ 中， $A B = A C, ∠ A C B = α$ ，点 $D$ 在边BC上，将线段DB绕点 $D$ 顺时针旋转得到线段DE（旋转角小于180°），连接BE，CE，以CE为底边在其上方作等腰三角形FEC，使 $∠ F C E = α$ .连接AF.

(1)、【尝试探究】
如图1，当a=60°时，易知AF-BE；如图2，当a=45°时，则AF与BE的数量关系为；

(2)、如图3，请判断∠EBC与 $∠ F A C$ 的数量关系，并说明理由：

(3)、【拓展应用】
如图4，当 $α = 3 0^{°}$ 且点B，E，F三点共线时.若 $A F = 2 \sqrt{3}, B D = \frac{1}{5} B C$ ，请求出CF的长.

查看试题解析

第一层杯子的个数x	1	2	3	4	5
杯子的总数y	1	3	6	10	15	…