广西壮族自治区南宁市天桃重点学校2023-2024年七年级下学期数学3月月考试卷
试卷更新日期:2024-03-30 类型:月考试卷
一、选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一个是正确的,请将所选选项填涂到答题卡相应位置)
-
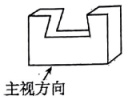
1. 2024的相反数是( )A、 B、2024 C、 D、2. 天宫二号空间实验室运行轨道距离地球约393000米,将393000用科学记数法表示应为( )A、 B、 C、 D、3. 榫卯是古代中国建筑、家具及其他器械的主要结构方式,是我国工艺文化精神的传承,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是( )
 A、
A、 B、
B、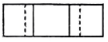 C、
C、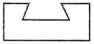 D、
D、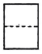 4. 下列方程中,解为的是( )A、 B、 C、 D、5. 以下命题为真命题的是( )A、同位角相等 B、相等的角是对顶角 C、过直线外一点有且只有一条直线与已知直线平行 D、两直线平行,同旁内角相等6. 下列各组单项式中,为同类项的是( )A、与 B、与 C、与 D、与7. 如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板),其依据是( )
4. 下列方程中,解为的是( )A、 B、 C、 D、5. 以下命题为真命题的是( )A、同位角相等 B、相等的角是对顶角 C、过直线外一点有且只有一条直线与已知直线平行 D、两直线平行,同旁内角相等6. 下列各组单项式中,为同类项的是( )A、与 B、与 C、与 D、与7. 如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板),其依据是( ) A、同旁内角互补,两直线平行 B、两直线平行,同旁内角互补 C、同位角相等,两直线平行 D、两直线平行,同位角相等8. 如图,直线与相交于点 , 平分 , 且 , 则为( )
A、同旁内角互补,两直线平行 B、两直线平行,同旁内角互补 C、同位角相等,两直线平行 D、两直线平行,同位角相等8. 如图,直线与相交于点 , 平分 , 且 , 则为( )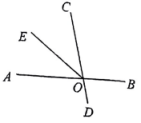 A、 B、 C、 D、9. 下列变形正确的是( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么10. 如图, , 为的中点,点在线段上,且 , 则的长度是( )
A、 B、 C、 D、9. 下列变形正确的是( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么10. 如图, , 为的中点,点在线段上,且 , 则的长度是( )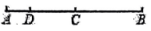 A、 B、 C、 D、11. 我国古代数学名著《算法统宗》中,有一道“群羊逐草”的问题,大意是:牧童甲在草原上放羊,乙牵着一只羊来,并问甲:“你的羊群有100只吗?”甲答:“如果在这群羊里加上同样的一群羊,再加上一群的一半,一群的四分之一,再加上你的一只,就是100只.”问牧童甲赶着多少只羊?若设这群羊有只,则下列方程中正确的是( )A、 B、 C、 D、12. 如图,长方形中有6个形状、大小相同的小长方形,且 , , 则图中阴影部分的面积为( )
A、 B、 C、 D、11. 我国古代数学名著《算法统宗》中,有一道“群羊逐草”的问题,大意是:牧童甲在草原上放羊,乙牵着一只羊来,并问甲:“你的羊群有100只吗?”甲答:“如果在这群羊里加上同样的一群羊,再加上一群的一半,一群的四分之一,再加上你的一只,就是100只.”问牧童甲赶着多少只羊?若设这群羊有只,则下列方程中正确的是( )A、 B、 C、 D、12. 如图,长方形中有6个形状、大小相同的小长方形,且 , , 则图中阴影部分的面积为( )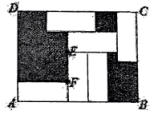 A、48 B、60 C、72 D、108
A、48 B、60 C、72 D、108二、填空题(本大题共6小题,每小题2分,共12分)
-
13. 比较大小:(填“>”、“<”或“=”).14. 一种商品每件盈利为元,售出60件,共盈利元(用含的式子表示).15. 如图,这是小明同学在体育课上跳远测量的方法,其中蕴含的数学道理是.
 16. 如图,直线 , 直线与、相交,若 , 则.
16. 如图,直线 , 直线与、相交,若 , 则.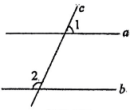 17. 如图,数轴上点为原点,点 , 分别表示数 , 2,则线段的长度为.
17. 如图,数轴上点为原点,点 , 分别表示数 , 2,则线段的长度为.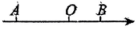 18. 有经验的渔夫用鱼叉捕鱼时,不会将鱼叉对准他看到的鱼,这是由于光从空气射入水中时,发生折射现象.如图,水面与底面平行,光线从空气射入水中时发生了折射,变成光线射到水底处,射线是光线的延长线, , , 则.
18. 有经验的渔夫用鱼叉捕鱼时,不会将鱼叉对准他看到的鱼,这是由于光从空气射入水中时,发生折射现象.如图,水面与底面平行,光线从空气射入水中时发生了折射,变成光线射到水底处,射线是光线的延长线, , , 则.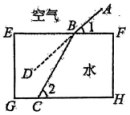
三、解答题(本大题共8小题,共72分,解答应写出文字说明,证明过程或演练步骤)
-
19. 计算:(1)、;(2)、.20. 解方程:(1)、;(2)、.21. 先化简再求值:
, 其中 ,
22. 如图,网格中每个小正方形的边长均为1,点、、均在小正方形的顶点,把三角形平移得到三角形 , 使点的对应点为点.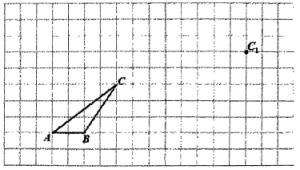 (1)、请在图中画出三角形;(2)、过点画出线段的垂线段,垂足为;(3)、三角形的面积为.23. 某校七年级利用劳动实践课开展创意点心制作比赛活动.小龙制作了一盒精美点心(共计6枚).现在他把6枚点心质量称重后统计列表如下:(单位:克)
(1)、请在图中画出三角形;(2)、过点画出线段的垂线段,垂足为;(3)、三角形的面积为.23. 某校七年级利用劳动实践课开展创意点心制作比赛活动.小龙制作了一盒精美点心(共计6枚).现在他把6枚点心质量称重后统计列表如下:(单位:克)第枚
1
2
3
4
5
6
质量
68.4
71.3
70.7
68.6
69.1
72
(1)、为了简化运算,小龙依据比赛的标准质量,他把超出部分记为正,不足部分记为负,列出下表(数据不完整),请你把表格补充完整:第枚
1
2
3
4
5
6
质量
(2)、按照比赛说明上标记,一盒点心的总质量合格标准为()克.那么,小龙制作的这盒点心的实际总质量是合格的.你知道为什么吗?请说明理由.24. 如图,、、分别在的三条边上,且 , .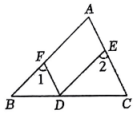 (1)、完成下列证明:
(1)、完成下列证明:证明:.
, ;
, ;
.
(2)、若 , 平分 , 求度数.25. 春节前某商场从厂家购进了甲、乙两种商品,甲种商品每件的进价比乙种商品每件的进价多20元.购进甲种商品4件与购进乙种商品5件的进价相同.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、该商场从厂家购进了甲、乙两种商品共100件,所用资金恰好为9200元.出售时,甲种商品在进价的基础上加价40%进行标价;乙商品按标价出售,则每件可获利30元.若按标价出售甲、乙两种商品,则全部售出后共可获利多少元?26. 【阅读思考】:如图①,已知.探究、、之间关系,小明添加了一条辅助线.解决了这道题.得到的结果是.证明过程如下:
如图①,过点作
.
,
.
.
, 即.
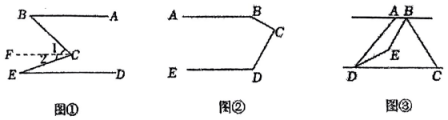 (1)、【理解应用】:如图②,已知 , 求的度数;(2)、【拓展探索】:如图③,已知 , 点在点的右侧, , 平分 , 平分 , , 所在的直线交于点 , 点在直线与之间.点在点的右侧,且 , .若 , 则度数为?(用含的代数式表示)
(1)、【理解应用】:如图②,已知 , 求的度数;(2)、【拓展探索】:如图③,已知 , 点在点的右侧, , 平分 , 平分 , , 所在的直线交于点 , 点在直线与之间.点在点的右侧,且 , .若 , 则度数为?(用含的代数式表示)