广东省广州市白云区2023-2024学年八年级下册开学考试数学试卷
试卷更新日期:2024-03-30 类型:开学考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列各式中,一定是二次根式的是( )A、 B、 C、 D、2. 下列各组数中,属于勾股数的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列二次根式中与是同类二次根式的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 若 , 则等于( )A、 B、 C、 D、6. 在中, , , 则( )A、 B、 C、 D、或7. 下列条件中,不能判定△ABC是直角三角形的是( )A、∠A=∠B+∠C B、a:b:c=5:12:13 C、a2=(b+c)(b-c) D、∠A:∠B:∠C=3:4:58. 如图,矩形的边在数轴上,点表示数 , 点表示数 , , 以点为圆心,的长为半径作弧与数轴负半轴交于点 , 则点表示的数为( )
 A、 B、 C、 D、9. 如图,在中, , , , Q是上一动点,过点Q作于M , 于N , , 则的长是( )
A、 B、 C、 D、9. 如图,在中, , , , Q是上一动点,过点Q作于M , 于N , , 则的长是( )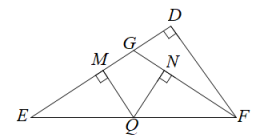 A、 B、 C、4 D、10. 如图,在中, , 以的各边为边作三个正方形,点落在上,若 , 空白部分面积为 , 则的长为( )
A、 B、 C、4 D、10. 如图,在中, , 以的各边为边作三个正方形,点落在上,若 , 空白部分面积为 , 则的长为( )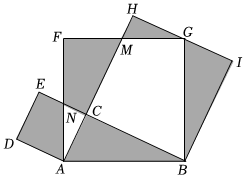 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
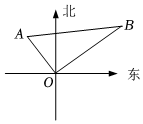
11. 若式子在实数范围内有意义,则的取值范围是 .12. 命题“同旁内角互补,两直线平行”的逆命题是 .13. 如图, , , , 点在点的北偏西方向,则点在点的方向.
 14. 已知实数 , , 在数轴上的位置如图所示,那么化简 .
14. 已知实数 , , 在数轴上的位置如图所示,那么化简 . 15. 如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为 m2 .
15. 如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为 m2 . 16. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .
16. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .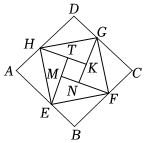
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算: .18. 若最简二次根式和是同类二次根式,求、平方和的算术平方根.19. 化简求值: , 其中 .20. 如图,正方形网格中的每个小正方形的边长都是 , 点、、均在格点上.
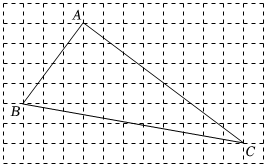 (1)、图中线段 , , ;(2)、求证:是直角三角形.21. 已知三角形三边之长能求出三角形的面积吗?
(1)、图中线段 , , ;(2)、求证:是直角三角形.21. 已知三角形三边之长能求出三角形的面积吗?海伦公式告诉你计算的方法是: , 其中表示三角形的面积, , , 分别表示三边之长,表示周长之半,即 .
我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦秦九韶公式”.
请你利用公式解答下列问题.
(1)、在中,已知 , , , 求的面积;(2)、计算中的边上的高.22. 如图,在中,过点作于点 .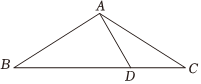 (1)、若 , , 求的长;(2)、在的条件下, , 求的面积.23. 如图所示,某两位同学为了测量风筝离地面的高度,测得牵线放风筝同学的头顶与风筝的水平距离为米已知牵线放风筝同学的身高为米,放出的风筝线长度为米其中风筝本身的长宽忽略不计
(1)、若 , , 求的长;(2)、在的条件下, , 求的面积.23. 如图所示,某两位同学为了测量风筝离地面的高度,测得牵线放风筝同学的头顶与风筝的水平距离为米已知牵线放风筝同学的身高为米,放出的风筝线长度为米其中风筝本身的长宽忽略不计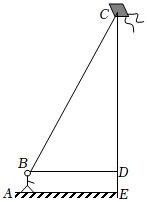 (1)、求此刻风筝离地面的高度;(2)、为了不与空中障碍物相撞,放风筝的同学要使风筝沿方向下降米,若该同学站在原地收线,请问他应该收回多少米?
(1)、求此刻风筝离地面的高度;(2)、为了不与空中障碍物相撞,放风筝的同学要使风筝沿方向下降米,若该同学站在原地收线,请问他应该收回多少米?