重庆市缙云教育联盟2023-2024学年高一下学期数学2月质检试卷
试卷更新日期:2024-03-30 类型:月考试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件2. 函数 的值域为( )A、 B、 C、 D、3. 我国著名数学家华罗庚先生曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休”在数学的学习和研究中,常用函数图象来研究函数性质,也常用函数解析式来分析函数图象的特征如函数的图象大致是( )A、
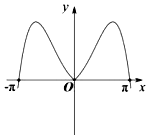 B、
B、 C、
C、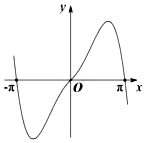 D、
D、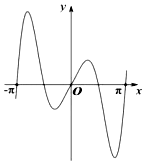 4. 对于两个不相等的实数、 , 规定符号表示、中的较大值,如:按照这个规定,方程的解集为( )A、 B、 C、 D、5. 若将函数 的图象向右平移 个单位,所得图象关于 轴对称,则 的最小正值是( )A、 B、 C、 D、6. 已知 , , 则的值是( )A、 B、 C、 D、7. 中,的最大值为( )A、 B、 C、 D、8. 已知 , , , 若当时,恒成立,则的最大值是( )A、 B、 C、 D、
4. 对于两个不相等的实数、 , 规定符号表示、中的较大值,如:按照这个规定,方程的解集为( )A、 B、 C、 D、5. 若将函数 的图象向右平移 个单位,所得图象关于 轴对称,则 的最小正值是( )A、 B、 C、 D、6. 已知 , , 则的值是( )A、 B、 C、 D、7. 中,的最大值为( )A、 B、 C、 D、8. 已知 , , , 若当时,恒成立,则的最大值是( )A、 B、 C、 D、二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
-
9. 若且 , , , 、 , , 则下列等式成立的是( )A、 B、 C、 D、10. 已知函数的定义域为 , 且对任意 , , 都有 , 且当时,恒成立,则( )A、函数是上的减函数 B、函数是奇函数 C、若 , 则的解集为 D、函数为偶函数11. 已知函数在区间上有且仅有个极小值点,且最多有个零点,则下列结论正确的是( )A、在上有且仅有个极大值点 B、如果是正整数,则或 C、的图象在上没有对称轴 D、在上单调递增
三、填空题:本题共3小题,每小题5分,共15分。
-
12. 已知函数 , 其中是自然对数的底数,则 .13. 设 , , 若 , 则 .14. 已知函数 , 若关于的方程恰有个不同的实数解,则的取值范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。