沪科版八年级下册勾股定理章节重难点题型梳理（一）
试卷更新日期：2024-03-29 类型：复习试卷
一、勾股定理面积证法
-
1. 数学家波利亚说过：“为了得到一个方程，我们必须把同一个量用两种不同的方法表示出来，即将一个量算两次，从而建立等量关系．”类似的，我们可以用两种不同的方法来表示同一个图形的面积，从而得到一个等式．
(1)、如图 ， 大正方形是由两个小正方形和两个形状大小完全相同的长方形拼成，请用两种不同的方法表示图中大正方形的面积．方法：；方法：；根据以上信息，可以得到的等式是；
(2)、如图 ， 大正方形是由四个边长分别为的直角三角形（为斜边）和一个小正方形拼成，请用两种不同的方法分别表示小正方形的面积，并推导得到之间的数量关系；(3)、在（）的条件下，若 ， 求斜边的值．2. 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”，如图是由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为 ， ， ． 若 ， 则下列关于 ， ， 的说法正确的是（ ）
A、 B、 C、 D、3. 用四个全等的直角三角形拼成如图①所示的大正方形，中间也是一个正方形．它是美丽的弦图．其中四个直角三角形的直角边长分别为a，b（a＜b），斜边长为c．
(1)、结合图①，说明：a2+b2＝c2；(2)、如图②，将这四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形ABCDEFGH．若该图形的周长为24，OH＝3，求该图形的面积；(3)、如图③，将八个全等的直角三角形紧密地拼接成正方形PQMN，记正方形PQMN、正方形ABCD、正方形EFGH的面积分别为S1、S2、S3 ， 若S1+S2+S3＝18，则S2＝ ．4. 如图，四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD，连结AC， 交BE于点P， 若正方形ABCD的面积为28，AE+BE＝7．则S△CFP-S△AEP的值是（ ）
A、3.5 B、4.5 C、5 D、5.55. 【教材呈现】如图是华师版八年级上册数学教材第117页的部分内容．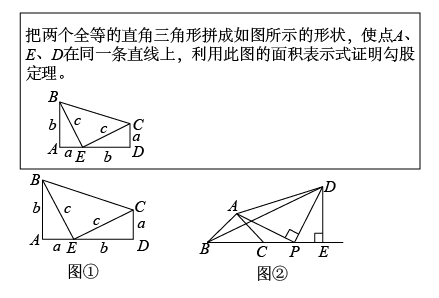
(1)、请结合图①，写出完整的证明过程；(2)、如图②，在等腰直角三角形中， ， ， P是射线BC上一点，以为直角边在边的右侧作 ， 使 ， ． 过点D作于点E，当时，则 ．6. 阅读下列材料，并完成相应任务．运用“双求法”证明勾股定理勾股定理表现了我国古人对数学的钻研精神和聪明才智，是我国古代数学的骄傲，它神秘而美妙，证法多样，是数学定理中证明方法最多的定理之一．勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a，b，c的式子表示同一个图形的面积”，由于同一个图形的面积相等，从而得到含a，b，c的恒等式，通过化简即可完成勾股定理的证明．数学上把这种方法称之为“双求法”．
下面是利用“双求法”证明勾股定理的一种思路：
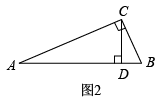
如图1，将两个全等的直角三角形与如图摆放，其中 ， ， ， ． 连接BD，过点D作BC延长线的垂线，垂足为F，容易得出 ， 用含a，b，c的式子表示出上面四个三角形的面积，就能完成勾股定理的证明．
(1)、任务一：请你根据上述材料中的思路证明勾股定理；(2)、任务二：请你用“双求法”解决下列问题；如图2，中， ， CD是AB边上的高，若 ， ， 则 ． （直接写出答案）
二、折叠问题
-
7. 如图，将长为4 cm、宽为2 cm的矩形纸片ABCD沿着EF翻折，使点A与点C重合，则折痕EF的长为cm.
8. 如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边的中点E处，点A落在点F处，折痕为MN，则线段CN的长是 （ ）
A、3cm B、4cm C、5cm D、6cm9. 如图，长方形ABCD中，点E是AD的中点，将△ABE沿BE向下折叠后得到△GBE，将BG延长线交直线 DC于点F.
(1)、若点G恰好落在边BC上，则AD与AB的数量关系是.(2)、如果点G在长方形ABCD的内部，如图所示.①试探究线段BF，AB，DF之间的数量关系，并说明理由；
②若DF=DC，AD=8，求AB的长度.
三、蚂蚁爬行{最短路径}
-
10. 如图，一只蚂蚁从长、宽都是3cm，高是8cm的长方体纸盒的A点沿纸盒面爬到B点，那么它所行的最短路线的长是（ ）
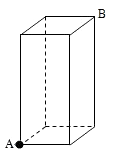A、(3 +8)cm B、10cm C、14cm D、无法确定11. 如图，一圆柱高 ， 底面周长是 ， 一只蚂蚁从点爬到点处吃食，要爬行的最短路程是（ ）
A、 B、 C、 D、12. 如图，若圆柱的底面周长是 ， 高是 ， 从圆柱底部处沿侧面缠绕一圈丝线到顶部处，则这条丝线的最小长度是 ．
13. 如图，圆柱形玻璃杯高为 ， 底面周长为 ， 在杯内壁离杯底的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿且与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为（ ） ． （杯壁厚度不计）
A、20 B、25 C、30 D、4014.
(1)、如图1，长方体的长为4cm，宽为3cm，高为12cm．求该长方体中能放入木棒的最大长度；(2)、如图2，长方体的长为4cm，宽为3cm，高为12cm．现有一只蚂蚁从点A处沿长方体的表面爬到点G处，求它爬行的最短路程；(3)、若将题中的长方体换成透明圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处．求蚂蚁吃到饭粒需要爬行的最短路程是多少？四、勾股定理几何应用
-
15. 如图，阴影部分表示以的各边为直径向上作三个半圆所组成的两个新月形，面积分别记作和 ． 若 ， 则长是（ ）
A、 B、 C、4 D、516. 如图，A ， B ， C ， D为矩形的四个顶点， ， ， 动点P ， Q分别从点A ， C同时出发，点P以的速度向点B移动，一直到达点B为止，点Q以的速度向点D移动，当点P到达点B时，点Q也随之停止运动，设点P的运动时间为 ． 当时，t的值为（ ）
A、 B、 C、 D、17. 如图，点在的边BC上，点是AC的中点，连结AD，DE，若AB ， 则CD的长为.
18. 在△ABC中，∠ACB=90°，D为△ABC内一点，连结BD，DC，延长DC至点E，使得CE=CD.
(1)、如图1，延长BC至点F，使得CF=BC，连结AF，EF.若AF⊥EF，求证：BD⊥AF.(2)、连结AE，交BD的延长线于点H，连结CH，请根据题意补全图2.若 ， 猜想线段CD与CH的数量关系，并证明.
