北师大版数学中考仿真模拟试题(二)
试卷更新日期:2024-03-29 类型:中考模拟
一、选择题(每题4分,共40分)
-
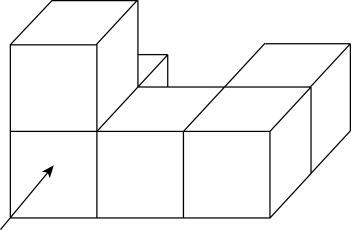
1. 的相反数是( )A、 B、 C、 D、2. 如图是由6个完全相同的小正方体搭成的几何体,其箭头所指方向为主视方向,则这个几何体的俯视图是( )
 A、
A、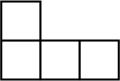 B、
B、 C、
C、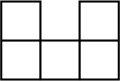 D、
D、 3. 如图,直线 , 点在上, , 垂足为若 , 则的度数为( )
3. 如图,直线 , 点在上, , 垂足为若 , 则的度数为( ) A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于x的不等式组 无实数解,则a的取值范围是( )A、 B、 C、 D、6. 如果一个三位数中任意两个相邻数字之差的绝对值不超过1,则称该三位数为“平稳数”.用 , , 这三个数字随机组成一个无重复数字的三位数,恰好是“平稳数”的概率为( )A、 B、 C、 D、7. 如图,在中,F是上一点,交于点E,的延长线交的延长线于点G, , , 则的长为( )
A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于x的不等式组 无实数解,则a的取值范围是( )A、 B、 C、 D、6. 如果一个三位数中任意两个相邻数字之差的绝对值不超过1,则称该三位数为“平稳数”.用 , , 这三个数字随机组成一个无重复数字的三位数,恰好是“平稳数”的概率为( )A、 B、 C、 D、7. 如图,在中,F是上一点,交于点E,的延长线交的延长线于点G, , , 则的长为( ) A、4 B、6 C、8 D、108. 在同一直角坐标系中,函数与的大致图象可能为( )A、
A、4 B、6 C、8 D、108. 在同一直角坐标系中,函数与的大致图象可能为( )A、 B、
B、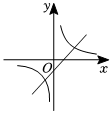 C、
C、 D、
D、 9. 如图,点A在函数的图象上,点B在函数的图象上,且轴,轴于点C , 则四边形的面积为( )
9. 如图,点A在函数的图象上,点B在函数的图象上,且轴,轴于点C , 则四边形的面积为( ) A、1 B、2 C、3 D、410. 如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( )
A、1 B、2 C、3 D、410. 如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 关于的分式方程有增根,则 .12. 已知、是方程的两根,则代数式的值为 .13. 学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前进.如图所示,和分别表示两人到小亮家的距离和时间的关系,则出发h后两人相遇.
 14. 如图,在矩形中,是边上一点,且 , 与相交于点 , 若的面积是 , 则的面积是 .
14. 如图,在矩形中,是边上一点,且 , 与相交于点 , 若的面积是 , 则的面积是 . 15. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:
15. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:①;
②若 , 则;
③若点 , 在抛物线上, , 且 , 则;
④当时,关于的一元二次方程必有两个不相等的实数根.
其中正确的是(填写序号).
16. 如图,在正方形中,点为边上一点,连接 , 将绕点顺时针旋转得到 , 在 , 上分别截取 , , 使 , 连接 , 交对角线于点 , 连接并延长交于点若 , , 则的长为 .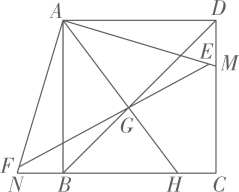
三、解答题(共8题,共86分)
-
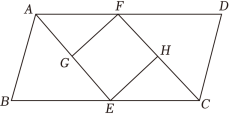
17.(1)、化简:(2)、利用数轴,确定不等式组的解集.18. 如图,在中,的平分线交于点E,的平分线交于点F,点G,H分别是和的中点.
 (1)、求证:;(2)、连接 . 若 , 请判断四边形的形状,并证明你的结论.19. 某中学为了了解学生最喜欢的课外活动,以便更好开展课后服务.随机抽取若干名学生进行了问卷调查.调查问卷如下:
(1)、求证:;(2)、连接 . 若 , 请判断四边形的形状,并证明你的结论.19. 某中学为了了解学生最喜欢的课外活动,以便更好开展课后服务.随机抽取若干名学生进行了问卷调查.调查问卷如下:调查问题
在下列课外活动中,你最喜欢的是( )(单选)
A.文学;B.科技;C.艺术;D.体育
填完后,请将问卷交给教务处.
根据统计得到的数据,绘制成下面的两幅不完整的统计图.
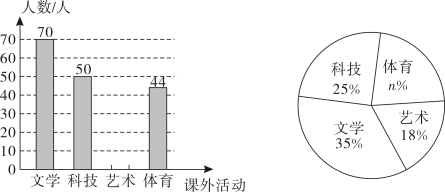
请根据统计图提供的信息,解答下面的问题:
(1)、本次调查采用的调查方式为(填写“普查”或“抽样调查”);(2)、在这次调查中,抽取的学生一共有人;扇形统计图中的值为;(3)、已知选择“科技”类课外活动的50名学生中有30名男生和20名女生.若从这50名学生中随机抽取1名学生座谈,且每名学生被抽到的可能性相同,则恰好抽到女生的概率是;(4)、若该校共有1000名学生参加课外活动,则估计选择“文学”类课外活动的学生有人.20. 如图,一艘轮船在处测得灯塔位于的北偏东方向上,轮船沿着正北方向航行20海里到达处,测得灯塔位于的北偏东方向上,测得港口位于的北偏东方向上.已知港口在灯塔的正北方向上.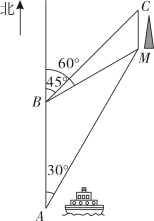 (1)、填空:度,度;(2)、求灯塔到轮船航线的距离(结果保留根号);(3)、求港口与灯塔的距离(结果保留根号).21. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .
(1)、填空:度,度;(2)、求灯塔到轮船航线的距离(结果保留根号);(3)、求港口与灯塔的距离(结果保留根号).21. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 . (1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.22. 如图,在中, , 的平分线交于点D,的平分线交于点E.以上的点O为圆心,为半径作 , 恰好过点E.
(1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.22. 如图,在中, , 的平分线交于点D,的平分线交于点E.以上的点O为圆心,为半径作 , 恰好过点E. (1)、求证:是的切线;(2)、若 , , 求的半径.23. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .
(1)、求证:是的切线;(2)、若 , , 求的半径.23. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
24. 【问题情境】在综合实践活动课上,李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动,两块三角板分别记作和 , 设 .
【操作探究】
如图1,先将和的边、重合,再将绕着点A按顺时针方向旋转,旋转角为 , 旋转过程中保持不动,连接 .
 (1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .
(1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .