【培优卷】2024年浙教版数学七年级下册第4章因式分解单元测试

试卷更新日期：2024-03-29 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 把多项式 $2 x^{2} + m x - 5$ 因式分解成 $(2 x + 5) (x - n)$ ，则m的值为（）

A、 $- 3$ B、3 C、5 D、7

查看试题解析
2. 已知 $4 x^{2} + 1$ 加上一个单项式后能成为一个整式的完全平方，给出下面四个单项式① $4 x$ ， ② $- 2 x$ ， ③ $-$ 1 ， ④ $4 x^{4}$ ，其中满足条件的共有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
3. 设n为整数，则 $\frac{1}{2} {(2 n + 1)}^{2} - 12 ， 5$ 一定能被（）

A、3 整除 B、4整除 C、6 整除 D、8整除

查看试题解析
4. 已知 $a^{2} (b + c) = b^{2} (a + c) = 2022$ ，且 $a \neq b$ ，则 - $a b c$ 的值为（）

A、2022 B、-2022 C、4044 D、-4044

查看试题解析
5. 把二次三项式2x²﹣8xy+5y²因式分解，下列结果中正确的是（）

A、（x﹣ $\frac{4 + \sqrt{6}}{2}$ y）（x﹣ $\frac{4 - \sqrt{6}}{2}$ y） B、（2x﹣4y+ $\sqrt{6}$ y）（x﹣ $\frac{4 + \sqrt{6}}{2}$ y） C、（2x﹣4y+ $\sqrt{6}$ y）（x﹣ $\frac{4 - \sqrt{6}}{2}$ y） D、2（x﹣ $\frac{4 - \sqrt{6}}{2}$ y）（x﹣ $\frac{4 + \sqrt{6}}{2}$ y）

查看试题解析
6. 定义：两个自然数的平方和加上这两个自然数乘积的两倍即可得到一个新的自然数，我们把这个新的自然数称为“完全数”.例如：2²+3²+2×2×3＝25，其中“25”就是一个“完全数”.则任取两个自然数可得到小于200且不重复的“完全数”的个数有（）

A、14个 B、15个 C、26个 D、60个

查看试题解析
7. 王林是一位密码编译爱好者，在他的密码手册中有这样一条信息： $x - 1$ ， $a - b$ ， 3， $x^{2} + 1$ ， a， $x + 1$ 分别对应六个字：底，爱，我，数，学，娄，现将 $3 a (x^{2} - 1) - 3 b (x^{2} - 1)$ 因式分解，结果呈现的密码信息可能是（）

A、我爱数学 B、爱娄底 C、我爱娄底 D、娄底数学

查看试题解析
8. 下列计算不正确的是（）

A、 ${(- \frac{2}{3})}^{2022} \times {(\frac{3}{2})}^{2021} = \frac{2}{3}$ B、若 $(x + 2) (x - 4) = x^{2} + n x - 8$ ，则 $n = - 2$ C、 $x^{2} + a x + 121$ 是一个完全平方式，则 $a$ 为 $\pm 22$ D、 $201 5^{2} - 2014 \times 2016 = - 1$

查看试题解析
9. 如图，边长为 $a$ 、 $b$ 的长方形周长为 $10$ ，面积为 $8$ ，则 $a^{2} b + a b^{2}$ 的值为（）

A、 $40$ B、 $60$ C、 $80$ D、 $100$

查看试题解析
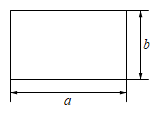10.
比较左、右两图的阴影部分面积，可以得到因式分解公式（）

A、a²-b²=（a+b）（a-b） B、（a+b）²=a²+2ab+b² C、（a-b）²=a²-2ab+b² D、a²-ab=a（a-b）

查看试题解析

二、填空题（每题4分，共24分）

11. 已知关于a的多项式a²+a+m(m为常数)可以用完全平方公式直接进行因式分解，则m的值为

查看试题解析
12. 多项式 $4 a^{2} + 9$ 加上一个单项式后，可化为一个整式的平方，则这个单项式是.（写一个即可）

查看试题解析
13. 将 $24 \times 25 \times 26 \times 27 + 1$ 表示成一个自然数的平方，则这个自然数是；若从一个正整数a开始，连续的四个整数的积再加上1，也可以用一个自然数的平方表示所得结果，即 $a \times (a + 1) \times (a + 2) \times (a + 3) + 1 = A^{2}$ ，其中a为正整数，那么这个自然数 $A =$ ．

查看试题解析
14. 生活中我们经常用到密码，如手机解锁、密码支付等 $.$ 为方便记忆，有一种用“因式分解”法产生的密码，其原理是：将一个多项式分解成多个因式，如：将多项式 $x^{3} - 9 x$ 分解结果为 $x (x + 3) (x - 3) .$ 当 $x = 20$ 时， $x + 3 = 23$ ， $x - 3 = 17$ ，此时可得到数字密码 $202317 .$ 将多项式 $x^{3} + m x^{2} + n x$ 因式分解后，利用题目中所示的方法，当 $x = 12$ 时可以得到密码 $121415$ ，则 $m n =$ ．

查看试题解析
15. 现有下列多项式：① $1 - a^{2}$ ；② $a^{2} - 2 a b + b^{2}$ ；③ $4 a^{2} - 9 b^{2}$ ；④ $3 a^{3} - 12 a$ ．在因式分解的过程中用到“平方差公式”来分解的多项式有．（只需填上题序号即可）

查看试题解析
16. 两名同学将一个二次三项式因式分解，甲同学因看错了一次项系数而分解成 $2 (x - 1) (x - 9)$ ；乙同学因看错了常数项而分解成 $2 (x - 2) (x - 4)$ ，请你将原多项式写出并把因式分解正确的结果写出来：．

查看试题解析

三、解答题（共8题，共66分）

17. 分解因式：

(1)、 $3 a^{2} - 6 a + 3 .$

(2)、 ${(a + b)}^{2} - 4 a^{2} .$

(3)、 $9 {(m + n)}^{2} - {(m - n)}^{2} .$

(4)、 $- 3 a^{2} x^{2} + 24 a^{2} x - 48 a^{2} .$

查看试题解析
18. 化简： $a + 1 + a (a + 1) + a {(a + 1)}^{2} + \dots + a （ a + 1 ）^{99}$ .

查看试题解析
19. 对任意一个三位数 $n$ ，如果 $n$ 满足各个数位上的数字互不相同，且都不为零，则称这个数为“真知数”，将 $n$ 的百位数字调到个位数字的后面，可以得到一个新的三位数，再将新三位数的百位数字调到个位数字的后面，可以得到另一个新的三位数，把这两个新数与原数 $n$ 的和与111的商记为 $F (n)$ .例如，123是“真知数”，将123的百位数字调到个位数字的后面得到231，再将231的百位数字调到个位数字的后面得到312，则 $F (123) = \frac{123 + 231 + 312}{111} = \frac{666}{111} = 6$ .

(1)、求 $F (421)$ ， $F (583)$ ；

(2)、已知 $s = 100 x + 21$ ， $t = 256 + y$ （ $1 \leq x \leq y \leq 9$ ， $x$ ， $y$ 为整数），若 $s$ 、 $t$ 均为“真知数”，且 $F (s) + F (t)$ 可被7整除，求 $t$ 的值.

查看试题解析
20. [阅读材料]分解因式： $x^{2} + x - 2$
解：把 $x = 1$ 代入 $x^{2} + x - 2$ ，发现此多项式的值为0，由此确定 $x^{2} + x - 2$ 中有因式 $x - 1$ ，可设 $x^{2} + x - 2 = (x - 1) (x + m) (m$ 为常数)，通过展开多项式或代入合适的 $x$ 的值即可求出 $m$ 的值.我们把这种分解因式的方法叫“试根法”.
根据以上阅读材料，完成下列问题：

(1)、请完成下列因式分解：
$x^{2} + x - 2 =$ ； $2 x^{2} - 5 x - 7 =$ ；

(2)、请你用“试根法”分解因式： $x^{3} + 3 x^{2} - 4$ ；

(3)、①若多项式 $x^{2} + m x - n (m ， n$ 为常数)分解因式后，有一个因式是 $(x - 2)$ ，求代数式 $\frac{9^{m}}{3^{n}}$ 的值；
②若多项式 $x^{4} + m x^{3} + n x - 16$ 含有因式 $(x - 2)$ 和 $(x + 1)$ ，求mn的值.

查看试题解析
21. 【发现】
任意五个连续整数的平方和是5的倍数.
【验证】

(1)、 $(- 1)^{2} + 0^{2} + 1^{2} + 2^{2} + 3^{2}$ 的结果是5的几倍?

(2)、设五个连续整数的中间一个为n，写出它们的平方和，并说明结果是5的倍数.

(3)、【延伸】
任意三个连续整数的平方和被3除的余数是几?请说明理由.

查看试题解析
22. 教材中的探究启发我们：通过用不同的方法计算同一图形的面积，可以探求出计算多项式乘法或分解因式的新途径.例如，选取图 1中的正方形、长方形硬纸片共 6 块，拼出一个如图2所示的长方形，计算它的面积可以得到相应的等式： $a^{2} + 3 a b + 2 b^{2} = (a + 2 b) (a + b)$ 或 $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ .

(1)、请根据图 3写出代数恒等式，并根据所写恒等式计算 ${(x - 2 y - 3)}^{2}$ .

(2)、若 $x^{2} + y^{2} + z^{2} = 1 ， x y + y z + x z = 3 ，$ 求 x +y+z的值.

(3)、试借助图1 的硬纸片，利用拼图的方法把二次多项式 $3 a^{2} + 7 a b + 2 b^{2}$ 分解因式，并把所拼的图形画在虚线方框内.

查看试题解析
23. 若x满足 $(5 - x) (x - 2) = 2$ ，求 $(x - 5)^{2} + (2 - x)^{2}$ 的值.
解：设 $5 - x = a ， x - 2 = b$ ，则 $(5 - x) (x - 2) = a b = 2 ， a + b = (5 - x) + (x - 2) = 3$ ，

所以 $(x - 5)^{2} + (2 - x)^{2} = (5 - x)^{2} + (x - 2)^{2} = a^{2} + b^{2} = (a + b)^{2} - 2 a b = 3^{2} - 2 \times 2 = 5$ .

请仿照上面的方法求解下面问题：

(1)、若 x 满足（x+2）（x-7）＝6，求（x+2）²+（x－7）²的值.

(2)、已知正方形 ABCD 的边长为 x，E，F 分别是 AD、DC 上的点，且 AE＝1，CF＝3，长方形 EMFD 的面积是 35，分别以 MF、DF 为边作正方形，求阴影部分的面积.

查看试题解析
24. 综合与实践

图1是一个长为a，宽为b的长方形．现有相同的长方形若干，进行如下操作：

(1)、用四块图1的小长方形不重叠地拼成一个如图2所示的正方形．请利用图2中阴影部分面积的不同表示方法，直接写出代数式 $(a + b)^{2}$ ， $(a - b)^{2}$ ， $a b$ 之间的等量关系；

(2)、将六块图1的小长方形不重叠地拼成一个如图3所示的长方形，通过不同方法计算阴影部分的面积，你能得到什么等式？请写出你的结论并用乘法法则证明这个等式成立；

(3)、现有图1的小长方形若干个，图4边长为a的正方形两个，边长为b的正方形两个请你用这些图形拼成一个长方形（不重叠），使其面积为 $2 a^{2} + 5 a b + 2 b^{2}$ ．画出你所拼成的长方形，并写出长方形的长和宽分别为多少．

查看试题解析

【培优卷】2024年浙教版数学七年级下册第4章因式分解 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

【培优卷】2024年浙教版数学七年级下册第4章因式分解单元测试