备考2024年中考数学计算能力训练8 解一元一次方程
试卷更新日期:2024-03-28 类型:二轮复习
一、选择题
-
1. 下列方程移项、系数化为1正确的是( )A、由3+x=5,得x=5+3 B、由2x+3=x+7,得2x+x=7+3 C、由7x=﹣4,得x=﹣ D、由y=2,得y=42. 关于x的方程3﹣ =0与方程2x﹣5=1的解相同,则常数a是( )A、2 B、﹣2 C、3 D、﹣33. 若 与 可以合并成一项,则 的值是( )A、2 B、4 C、8 D、164. 把方程 去分母,下列变形正确的是( )A、 B、 C、 D、5. 解方程3-(x-6)=5(x-1)时,去括号正确的是( )A、3-x+6=5x+5 B、3-x-6=5x+1 C、3-x+6=5x-5 D、3-x-6=5x+16. 将方程中分母化为整数,正确的是( )A、 B、 C、 D、7. 下列等式变形正确的是( )A、若-3x=5,则x= B、若 ,则2x+3(x-1)=1 C、若5x-6=2x+8,则5x+2x=8+6 D、若3(x+1)-2x=1则3x+3-2x=18. 在解方程 时,去分母后正确的是( )A、 B、 C、 D、9. 下列方程的变形中正确的是( )A、由2x+6=-3移项得2x=-3+6 B、由 去分母得(x-3)-(2x+1)=6 C、由2(x+1)-(x-1)=4去括号得2x+2-x+1=4 D、由7x=4系数化为1得10. 已知关于的一元一次方程的解为 , 那么关于的一元一次方程的解为( )A、 B、 C、1 D、2
二、填空题
-
11. 关于的方程的解是 , 则的值是.12. 已加关于x的一元一次方程2021x-3=4x+3b的解为x=7,则关于y的一元一次方程2021(1-y)+3=4(1- y)-3b的解为y = .13. 若3xm+5y3与x2yn的差仍为单项式,则m+n= .14. 若是关于x的方程的解,则 .15. 如图是一个数表,现用一个矩形在数表中任意框出
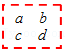 4个数,当a+b+c+d=32时,a= .
4个数,当a+b+c+d=32时,a= .  16. 小明做作业时,不小心将方程中的一个常数污染了看不清楚,小芳告诉他该方程的解是负数,并且这个常数是负整数,该方程的解是 .17. 若关于x的方程 , 无论k为任何数时,它的解总是x=2,那么m+n= .18. 点Q的横坐标为一元一次方程的解,纵坐标为的值,其中a,b满足二元一次方程组 , 则点Q关于y轴对称点的坐标为 .
16. 小明做作业时,不小心将方程中的一个常数污染了看不清楚,小芳告诉他该方程的解是负数,并且这个常数是负整数,该方程的解是 .17. 若关于x的方程 , 无论k为任何数时,它的解总是x=2,那么m+n= .18. 点Q的横坐标为一元一次方程的解,纵坐标为的值,其中a,b满足二元一次方程组 , 则点Q关于y轴对称点的坐标为 .三、计算题
-
19. 解方程: .20. 已知关于x的方程 的解是关于x的方程5x+5=5a的解相同,求a的值.21. 当m满足什么条件时,关于x的方程|x-3|-|x-7|=m有一解?有无数多个解?无解?如果方程有解,请求出方程的解。22. 方程2-3(x+1)=0的解与关于x的方程 的解互为倒数,求k的值.
23. 已知x=-3是|2x-1|-3|m|=-1的解,求代数式3m2-m-1的值.
24. 方程 与方程 的解相同,求m的值.25. 小红在解方程时,第一步出现了错误: (1)、请在相应的方框内用横线划出小红的错误处.(2)、写出你的解答过程.
(1)、请在相应的方框内用横线划出小红的错误处.(2)、写出你的解答过程.四、解答题
-
26. 已知方程是关于的一元一次方程.(1)、求的值;(2)、若关于的一元一次方程的解与关于的一元一次方程的解互为倒数,求的值.27. 下图是一个运算程序:
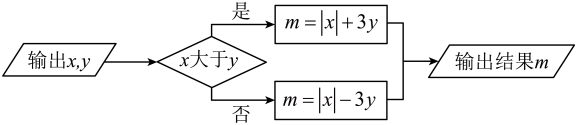 (1)、若 , , 求的值;(2)、若 , 输出结果的值是输入的值的两倍,求的值.28.(1)、计算:;(2)、下面是小明同学解方程的过程,请认真阅读,并完成相应的任务.
(1)、若 , , 求的值;(2)、若 , 输出结果的值是输入的值的两倍,求的值.28.(1)、计算:;(2)、下面是小明同学解方程的过程,请认真阅读,并完成相应的任务.解:去分母,得 . 第一步
去括号,得 . 第二步
移项,得 . 第三步
合并同类项.得 . 第四步
系数化为1,得 . 第五步
任务一:①解答过程中,第 ▲ 步开始出现了错误,产生错误的原因是 ▲ ;
②第三步变形的依据是 ▲ .
任务二:①该一元一次方程的解是 ▲ ;
②写出一条解一元一次方程时应注意的事项.
29. 小明在解关于x的方程3a-2x=11时,误将-2x看成了+2x得到的解为x=-2,请你帮小明算一算,方程正确的解为多少?
30. 方程是含有未知数的等式,使等式成立的未知数的值称为方程的“解”.方程的解的个数会有哪些可能呢?(1)、根据“任何数的偶数次幂都是非负数”可知:关于x的方程x2+1=0的解的个数为;(2)、根据“几个数相乘,若有因数为0,则乘积为0”可知方程(x+1)(x﹣2)(x﹣3)=0的解不止一个,直接写出这个方程的所有解;(3)、结合数轴,探索方程|x+1|+|x﹣3|=4的解的个数;(写出结论,并说明理由)(4)、进一步可以发现,关于x的方程|x﹣m|+|x﹣3|=2m+1(m为常数)的解的个数随着m的变化而变化…请你继续探索,直接写出方程的解的个数与对应的m的取值情况.