2024年北师大版数学八(下)期中专项复习3 线段的垂直平分线和角平分线
试卷更新日期:2024-03-28 类型:复习试卷
一、选择题
-
1. 如图,为线段的垂直平分线上一点,若 , 则的长为( )
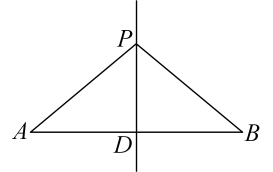 A、 B、 C、 D、2. 如图在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N , 再分别以M、N为圆心,大于 MN的长为半径画弧,两弧交于点P , 作射线AP交BC于点D , 若CD=2,AB=8,则△ABD的面积是( )
A、 B、 C、 D、2. 如图在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N , 再分别以M、N为圆心,大于 MN的长为半径画弧,两弧交于点P , 作射线AP交BC于点D , 若CD=2,AB=8,则△ABD的面积是( ) A、16 B、32 C、8 D、43. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( )
A、16 B、32 C、8 D、43. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( ) A、25 B、22 C、20 D、144. 如图,在中,AD平分 , 若 , , 则( )
A、25 B、22 C、20 D、144. 如图,在中,AD平分 , 若 , , 则( )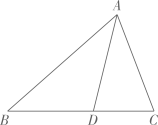 A、25:16 B、5:4 C、16:25 D、4:55. 在三角形ABC中, , DE垂直平分斜边AB,分别交AB,BC于D,E.若 , 求( )
A、25:16 B、5:4 C、16:25 D、4:55. 在三角形ABC中, , DE垂直平分斜边AB,分别交AB,BC于D,E.若 , 求( ) A、120° B、130° C、140° D、150°6. 如图,在中, , , 线段的垂直平分线分别交 , 于点 , , 连接若 , 则的长为( )
A、120° B、130° C、140° D、150°6. 如图,在中, , , 线段的垂直平分线分别交 , 于点 , , 连接若 , 则的长为( )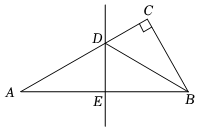 A、 B、 C、 D、7. 如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=5,则DF的长度是( )
A、 B、 C、 D、7. 如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=5,则DF的长度是( ) A、3 B、4 C、5 D、68. 如图,在中,已知 , , 的周长为 , 分别以A、B两点为圆心,大于的长为半径画弧,两弧相交于点M , N , 连接与相交于点D , 则的周长为( )
A、3 B、4 C、5 D、68. 如图,在中,已知 , , 的周长为 , 分别以A、B两点为圆心,大于的长为半径画弧,两弧相交于点M , N , 连接与相交于点D , 则的周长为( )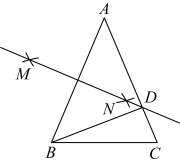 A、 B、 C、 D、9. 如图,中,分别是其角平分线和中线,过点C作于F , 连接 , 则线段的长为( )
A、 B、 C、 D、9. 如图,中,分别是其角平分线和中线,过点C作于F , 连接 , 则线段的长为( ) A、 B、2 C、 D、310. 如图,在△ABD中,AD=AB,∠DAB=90°,在△ACE中,AC=AE,∠EAC=90°,CD,BE相交于点F,有下列四个结论:①∠BDC=∠BEC;②FA平分∠DFE;③DC⊥BE;④DC=BE.其中,正确的结论有( )
A、 B、2 C、 D、310. 如图,在△ABD中,AD=AB,∠DAB=90°,在△ACE中,AC=AE,∠EAC=90°,CD,BE相交于点F,有下列四个结论:①∠BDC=∠BEC;②FA平分∠DFE;③DC⊥BE;④DC=BE.其中,正确的结论有( ) A、①②③④ B、①③④ C、②③ D、②③④
A、①②③④ B、①③④ C、②③ D、②③④二、填空题
-
11. 已知在中, , , , 则边上的中线 .12. 如图,在中,是边上的高,平分 , 交于点 , 已知, , , 则的面积等于 .
 13. 如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E.若△ABD的周长为13,BE=5,则△ABC的周长为 .
13. 如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E.若△ABD的周长为13,BE=5,则△ABC的周长为 .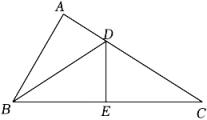 14. 如图,的两直角边 , 长分别为 , , 其三条角平分线交于点 , 将分为三个三角形,则:: .
14. 如图,的两直角边 , 长分别为 , , 其三条角平分线交于点 , 将分为三个三角形,则:: . 15. 如图,在中, , 的垂直平分线交于点 , 交边于点 , 的周长等于 , 则的长等于 .
15. 如图,在中, , 的垂直平分线交于点 , 交边于点 , 的周长等于 , 则的长等于 .
三、作图题
-
16. 如图,在中, .
 (1)、用尺规作的平分线,交于点不写作法,保留作图痕迹;(2)、若 , , 求边上的高的长度.17. 如图,已知 , , , 为上一点,且到、两点的距离相等.
(1)、用尺规作的平分线,交于点不写作法,保留作图痕迹;(2)、若 , , 求边上的高的长度.17. 如图,已知 , , , 为上一点,且到、两点的距离相等. (1)、用直尺和圆规,作出点的位置不写作法,保留作图痕迹;(2)、连结 , 若 , 求的度数.
(1)、用直尺和圆规,作出点的位置不写作法,保留作图痕迹;(2)、连结 , 若 , 求的度数.四、解答题
-
18.
如图,在△ABC中,∠C=90°,∠A=36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E.求∠EBC的度数.
 19. 在中, , 平分 , 交于点 .
19. 在中, , 平分 , 交于点 . (1)、如图 , 若 , 求的度数;(2)、如图 , 在上取点 , 连接交于点 , 连接、 .
(1)、如图 , 若 , 求的度数;(2)、如图 , 在上取点 , 连接交于点 , 连接、 .给出四个关系:
①;
②;
③平分;
④ .
请从中选择一个作为条件,证明垂直平分 .
你选的条件是 ▲ , 请写出推理的过程.
20. 如图,中,平分 , 的中垂线交于点 , 交于点 , 连接 . 若 , , 求的度数.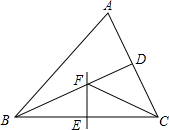
五、综合题
-
21. 如图,AD为等腰△ABC的顶角∠BAC的平分线,∠ABC=50°,在线段AD上取一点E.使得∠ACE=20°,在线段CE上取一点F,使得∠FBC=10°,连接BE,AF.(1)、∠EBF=度,∠EBA=度,∠BFE=度;(2)、求证:BA=BF;(3)、BE与AF的位置关系为 (直接写出).


