2024年北师大版数学八(下)期中专项复习2 直角三角形
试卷更新日期:2024-03-28 类型:复习试卷
一、选择题
-
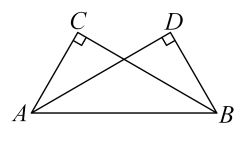
1. 已知一个三角形的三边长度如下,则能够判断这个三角形是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,2. 下列命题的逆命题是真命题的是( )A、相等的角是对顶角 B、等边三角形是锐角三角形 C、若 , 则 D、全等三角形的面积相等3. 如图, , , , 点A在点O的北偏西方向,则点B在点O的( )
 A、北偏东 B、北偏东 C、东偏北 D、东偏北4. 下列说法中正确的是( ).A、在△ABC中,AB= , AC= , BC=1,△ABC是直角三角形 B、三个角都相等的三角形是等边三角形. C、若等腰三角形ABC的两边长a,b满足(a-3)2+|b-6|=0,则△ABC的周长为12 D、用反证法证明命题,“求证: 等腰三角形的底角必为锐角”,第一步应先假设“等腰三角形的底角为锐角”5. 如图,在中, , , 平分交于点D, , 垂足为E,且 , 则的周长为( )
A、北偏东 B、北偏东 C、东偏北 D、东偏北4. 下列说法中正确的是( ).A、在△ABC中,AB= , AC= , BC=1,△ABC是直角三角形 B、三个角都相等的三角形是等边三角形. C、若等腰三角形ABC的两边长a,b满足(a-3)2+|b-6|=0,则△ABC的周长为12 D、用反证法证明命题,“求证: 等腰三角形的底角必为锐角”,第一步应先假设“等腰三角形的底角为锐角”5. 如图,在中, , , 平分交于点D, , 垂足为E,且 , 则的周长为( ) A、 B、 C、 D、6. 满足下列条件的中,不是直角三角形的是( )A、 B、 C、 D、7. 下列命题的逆命题是假命题的是( )A、两直线平行,同位角相等 B、全等三角形的对应角相等 C、等边三角形三个角相等 D、直角三角形中,斜边的平方等于两直角边的平方和8. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )
A、 B、 C、 D、6. 满足下列条件的中,不是直角三角形的是( )A、 B、 C、 D、7. 下列命题的逆命题是假命题的是( )A、两直线平行,同位角相等 B、全等三角形的对应角相等 C、等边三角形三个角相等 D、直角三角形中,斜边的平方等于两直角边的平方和8. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )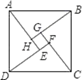 A、2 B、4 C、6 D、89. 在△ABC中,三边长满足b2﹣a2=c2 , 则互余的一对角是( )A、∠A与∠B B、∠B与∠C C、∠A与∠C D、以上都不正确10. 如图,正方形小方格边长为1,则网格中的△ABC是( )
A、2 B、4 C、6 D、89. 在△ABC中,三边长满足b2﹣a2=c2 , 则互余的一对角是( )A、∠A与∠B B、∠B与∠C C、∠A与∠C D、以上都不正确10. 如图,正方形小方格边长为1,则网格中的△ABC是( )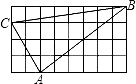 A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对二、填空题
-
11. 如图,已知 , 请你添加一个条件,使得≌你添加的条件是:写出一个符合题意的即可
 12. 在Rt△ABC中,已知∠C=90°,∠B=46°,则∠A的度数为 .13. 命题“若 , 则”的逆命题是.14. 如图,在Rt△ACB中,∠ACB=90°,∠B=30°,AC=2.若将△ABC绕点C按逆时针方向旋转得到△A'B'C,点A的对应点为A',且点A'恰好在AB边上,则点B'与点B之间的距离为
12. 在Rt△ABC中,已知∠C=90°,∠B=46°,则∠A的度数为 .13. 命题“若 , 则”的逆命题是.14. 如图,在Rt△ACB中,∠ACB=90°,∠B=30°,AC=2.若将△ABC绕点C按逆时针方向旋转得到△A'B'C,点A的对应点为A',且点A'恰好在AB边上,则点B'与点B之间的距离为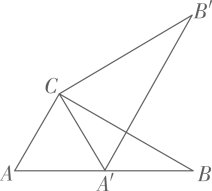 15. 如图,△ABC中,D为BC上一点,且BD=3,DC=AB=5,AD=4,则AC=.
15. 如图,△ABC中,D为BC上一点,且BD=3,DC=AB=5,AD=4,则AC=.
三、解答题
-
16. 如图,在中,AB=AC,BC=15,D是AB上一点,BD=9,CD=12,求AC长.
 17. 如图,在四边形ABCD中,已知AB=5,BC=3,CD=6,AD=2 ,若AC⊥BC,求证:AD∥BC.
17. 如图,在四边形ABCD中,已知AB=5,BC=3,CD=6,AD=2 ,若AC⊥BC,求证:AD∥BC.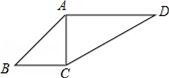 18. 如图,在边长为1的正方形网格上,有一个△ABC,它的各个顶点都在格子上,△ABC是直角三角形吗?为什么?
18. 如图,在边长为1的正方形网格上,有一个△ABC,它的各个顶点都在格子上,△ABC是直角三角形吗?为什么?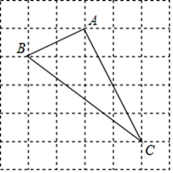
四、综合题
-
19. 如图,在4×3正方形网格中,每个小正方形的边长都是1.
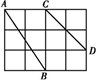 (1)、分别求出线段AB,CD的长度;(2)、在图中画线段EF,使得EF的长为 ,以AB,CD,EF三条线段能否构成直角三角形,并说明理由.20. 如图,已知在△ABC中,AB=AC=13cm,D是AB上一点,且CD=12cm,BD=8cm.
(1)、分别求出线段AB,CD的长度;(2)、在图中画线段EF,使得EF的长为 ,以AB,CD,EF三条线段能否构成直角三角形,并说明理由.20. 如图,已知在△ABC中,AB=AC=13cm,D是AB上一点,且CD=12cm,BD=8cm.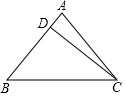 (1)、求证:△ADC是直角三角形;(2)、求BC的长21. 如图,点A,D,B,E在同一直线上, .
(1)、求证:△ADC是直角三角形;(2)、求BC的长21. 如图,点A,D,B,E在同一直线上, .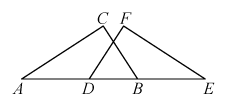 (1)、求证:;(2)、 ,求的度数.22. 如图,已知等腰三角形 的底边 长为10,点 是 上的一点,其中 。
(1)、求证:;(2)、 ,求的度数.22. 如图,已知等腰三角形 的底边 长为10,点 是 上的一点,其中 。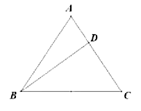 (1)、求证: ;(2)、求 的长。23. 【问题背景】17世纪有着“业余数学家之王”美誉的法国律师皮耶·德·费马,提出一个问题:求作三角形内的一个点,使它到三角形三个顶点的距离之和最小后来这点被称之为“费马点”.
(1)、求证: ;(2)、求 的长。23. 【问题背景】17世纪有着“业余数学家之王”美誉的法国律师皮耶·德·费马,提出一个问题:求作三角形内的一个点,使它到三角形三个顶点的距离之和最小后来这点被称之为“费马点”.如图,点是内的一点,将绕点逆时针旋转60°到 , 则可以构造出等边 , 得 , , 所以的值转化为的值,当 , , , 四点共线时,线段的长为所求的最小值,即点为的“费马点”.
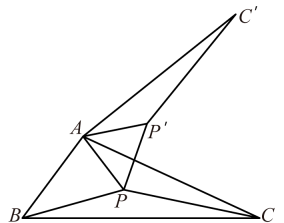 (1)、【拓展应用】
(1)、【拓展应用】如图1,点是等边内的一点,连接 , , , 将绕点逆时针旋转60°得到.
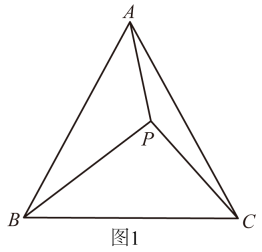
①若 , 则点与点之间的距离是 ▲ ;
②当 , , 时,求的大小;
(2)、如图2,点是内的一点,且 , , , 求的最小值.