2024年北师大版数学八（下）期中专项复习1 等腰三角形

试卷更新日期：2024-03-28 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ ，且 $B C = 4$ ，则BD长为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 如图，矩形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点 $O .$ 若 $∠ A O B = 60 °$ ， $B D = 8$ ，则 $A B$ 的长为（）

A、 $3$ B、 $4$ C、 $4 \sqrt{3}$ D、 $5$

查看试题解析
3. 已知一个等腰三角形两内角的度数之比为1：4，则这个等腰三角形顶角的度数为（）

A、20°或100° B、120° C、20°或120° D、36°

查看试题解析
4. 已知等腰三角形有两条边的长分别是3，7，则这个等腰三角形的周长为（）

A、17 B、13 C、17或13 D、10

查看试题解析
5. 如图， $D$ 为 $△ A B C$ 内一点，过点 $D$ 的直线 $E F$ 与边 $A B$ ， $A C$ 分别交于点 $F$ ， $E$ ，若点 $E$ ，点 $F$ 恰好分别在 $C D$ ， $B D$ 的垂直平分线上，记 $∠ D B F = α$ ， $∠ A + 2 ∠ D C E = β$ ，则 $α$ ， $β$ 满足的关系式为（）

A、 $β - α = 90 °$ B、 $β - 2 α = 90 °$ C、 $2 α + β = 180 °$ D、 $2 β + α = 180 °$

查看试题解析
6. 已知等腰三角形周长为 $13 c m$ ，其中一边长为 $3 c m$ ，则该等腰三角形的腰长为（）

A、 $7 c m$ B、 $3 c m$ C、 $5 c m$ 或 $3 c m$ D、 $5 c m$

查看试题解析
7. 用反证法证明：在△ABC中，∠A、∠B、∠C中不能有两个角是钝角时，假设，∠A、∠B、∠C中有两个角是钝角，令∠A＞90°，∠B＞90°，则所得结论与下列四个选项相矛盾的是（）

A、已知 B、三角形内角和等于180° C、钝角三角形的定义 D、以上结论都不对

查看试题解析
8. 如图，在Rt△ABC中．∠ACB＝90°，CD⊥AB于D，∠BAC的平分线AF交CD于点E，交BC于F，CM⊥AF于M，CM的延长线交AB于点N，下列四个结论：①AC＝AN；②EN＝FC；③EN∥BC；④∠ABC＝45°，其中正确的结论有（）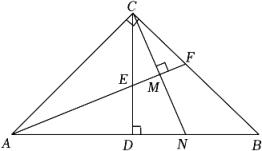

A、①②④ B、①③④ C、①②③ D、①②③④

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ A B C$ 和 $∠ A C B$ 的平分线交于点 $E$ ，过点 $E$ 作 $M N / / B C$ 交 $A B$ 于 $M$ ，交 $A C$ 于 $N$ ，若 $B M + C N = 9$ ，则线段 $M N$ 的长为（）

A、 $6$ B、 $7$ C、 $8$ D、 $9$

查看试题解析
10. 若等腰三角形的底角为 $48 °$ ，则这个等腰三角形的顶角度数为（）

A、 $66 °$ B、 $84 °$ C、 $48 °$ D、 $68 °$

查看试题解析

二、填空题

11. 等腰三角形一腰上的高与另一腰的夹角是 $46 °$ ，则它的底角度数是．

查看试题解析
12. 如图，在四边形 $A B C D$ 中， $∠ B A D = 90 °$ ， $A B = B C = A D = 5$ ，对角线 $A C ⊥ C D$ ，则线段 $C D$ 的长为．

查看试题解析
13. 一个等腰三角形的周长为24，其中它的腰长 $x$ 为自变量，底边长 $y$ 为因变量，则用 $x$ 表示 $y$ 的关系式是.

查看试题解析
14. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $∠ B A C$ 的平分线交 $B C$ 于点 $D$ ， $D E ∥ A B$ ，交 $A C$ 于点 $E$ ， $D F ⊥ A B$ 于点 $F$ ，若 $D E = 5$ ， $D F = 3$ ，则 $A F$ 的长为．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A E ⊥ B D$ 于E， $∠ D A E = 3 ∠ E A B$ ，则 $∠ E A C$ 的度数为度．

查看试题解析

三、解答题

16. 如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D，点E是AB的中点，连接DE．求证：△ABD是等腰三角形．

查看试题解析
17. 如图，△ABC是等腰三角形，∠B=∠C，AD是底边BC上的高，DE∥AB交AC于点E．试说明△ADE是等腰三角形．

查看试题解析
18. 等腰三角形的一个底角是顶角的4倍，求这个等腰三角形各角度数．

查看试题解析
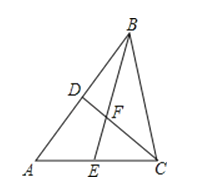
19.
用反证法证明命题“已知D，E分别为△ABC的边AB，AC上的点，BE，CD交于点F，则BE，CD不能互相平分”是真命题．

查看试题解析
20.
已知：如图，△ABO是等边三角形，CD∥AB，分别交AO、BO的延长线于点C、D．求证：△OCD是等边三角形．

查看试题解析

四、综合题

21. 如图，在等边三角形 $A B C$ 中，点 $D$ ， $E$ 分别在边 $B C$ ， $A C$ 上，且 $D E / / A B$ ，过点 $E$ 作 $E F ⊥ D E$ ，交 $B C$ 的延长线于点 $F$ ．

(1)、求 $∠ F$ 的度数；

(2)、若 $C D = 2$ ，求 $D E$ 的长．

查看试题解析
22. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．

(1)、求∠F的度数；

(2)、若CD＝2，求DE的长．

查看试题解析
23. 如图，在△ABC中，∠ABC＝70°，AB＝AC＝8，D为BC中点，点N在线段AD上， $N M ∥ A C$ 交AB于点M，BN＝3．

(1)、求∠CAD度数；

(2)、求△BMN的周长．

查看试题解析
24. 已知，在等边三角形 $A B C$ 中，点E在 $A B$ 上，点D在 $C B$ 的延长线上，且 $E D = E C$ ．

(1)、【特殊情况，探索结论】如图1，当点E为 $A B$ 的中点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你直接写出结论： $A E$ $D B$ （填“＞”、“＜”或“＝”）．

(2)、【特例启发，解答题目】如图2，当点E为 $A B$ 边上任意一点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你写出结论，并说明理由． $A E$ ▲ $D B$ （填“＞”、“＜”或“＝”）；理由如下，过点E作 $E F ∥ B C$ ，交 $A C$ 于点F ．（请你完成以下解答过程）．

(3)、【拓展结论，设计新题】在等边三角形 $A B C$ 中，点E在直线 $A B$ 上，点D在线段 $C B$ 的延长线上，且 $E D = E C$ ，若 $△ A B C$ 的边长为1， $A E = 2$ ，求 $C D$ 的长（直接写出结果）．

查看试题解析