【培优卷】2024年浙教版数学七年级下册4.3用乘法公式分解因式同步练习

试卷更新日期：2024-03-28 类型：同步测试

进入出卷网下载

一、选择题

1. 设 n是任意正整数，代入式子 n³-n中计算时，四名同学算出以下四个结果，其中正确的结果可能是（）

A、388 947 B、388 944 C、388 953 D、388 949

查看试题解析
2. 若 $202 2^{2022} - 202 2^{2020} = 2023 \times 202 2^{n} \times 2021$ ，则n的值是（）

A、2023 B、2022 C、2021 D、2020

查看试题解析
3. 若 $c^{2} - a^{2} - 2 a b - b^{2} = 10$ ， $a + b + c = - 5$ ，则 $a + b - c$ 的值是（）

A、2 B、5 C、20 D、9

查看试题解析
4. 已知x，y为任意有理数，记M = x²+y² ， N = 2xy，则M与N的大小关系为（）

A、M>N B、M≥N C、M≤N D、不能确定

查看试题解析
5. 已知 $m^{2} = 3 n + a ， n^{2} = 3 m + a ， m \neq n$ ，则 $m^{2} + 2 m n + n^{2}$ 的值为（）

A、9 B、6 C、4 D、2

查看试题解析
6. 已知长方形的边长分别为 a，b，周长为 14，面积为10，则 $a^{2} b + {ab}^{2}$ 的值为（）

A、35 B、70 C、140 D、280

查看试题解析
7. 生活中我们经常用到密码，如到银行取款．有一种用“因式分解”法产生的密码，方便记忆，其原理是：将一个多项式分解因式，如多项式 $x^{4} - y^{4}$ 因式分解的结果是 $(x - y) (x + y) (x^{2} + y^{2})$ ，当取 $x = 9$ ， $y = 9$ 时，各个因式的值是： $(x - y) = 0$ ， $(x + y) = 18$ ， $(x^{2} + y^{2}) = 162$ ，于是就可以把“018162”作为一个六位数的密码．类似地，对于多项式 $4 x^{3} - x y^{2}$ ，当取 $x = 10$ ， $y = 10$ 时，用上述方法可以产生一个六位数密码．则这个密码可以是（）

A、102030 B、103020 C、101030 D、102010

查看试题解析
8. 如图，大正方形的边长为a ，小正方形的边长为b ，若用x ， y表示四个长方形的两边长（ $x > y$ ），观察图案及以下关系式：① $x - y = b$ ；② $x + y = a$ ；③ $x^{2} - y^{2} = a b$ ；④ $x^{2} + y^{2} = \frac{a^{2} + b^{2}}{2}$ ；⑤ $x y = \frac{a^{2} - b^{2}}{2}$ ；其中正确的关系式有（）

A、①②③④ B、①②③⑤ C、①②④⑤ D、①③④⑤

查看试题解析

二、填空题

9. 设多项式x³﹣x﹣a与多项式x²+x﹣a有公因式，则a＝．

查看试题解析
10. 如果多项式9x²+1加上一个单项式后，使它能成为一个多项式的平方，那么加上的多项式可以是(应写尽写)

查看试题解析
11. 若 $m^{2} = n + 2023 ， n^{2} = m + 2023$ ，且 $m \neq n$ ，则代数式 $m^{3} - 2 m n + n^{3}$ 的值为．

查看试题解析
12. 有一种用“因式分解”法产生的密码，其原理是：将一个多项式分解因式，如多项式x⁴-y⁴因式分解的结果是(x-y)(x+y)(x²+y²)，当取x=4，y=4时，各个因式的值是：x-y=0，x+y=8x²+y²=32，于是就可以把“0832”作为一个密码，我们把上述密码中的“0”、“8”、“32”分别叫做这串密码的第一位因式码、第二位因式码、第三位因式码．类似地，对于多项式xy+xy⁴因式分解的结果是xy(x+y)(x²-xy+y²)，当它的第一位因式码xy和第二位因式码(x+y)构成的数是“127”时，它的第三位因式码(x²-xy+y²)是.

查看试题解析

三、解答题

13. 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如：4=2²﹣0² ， 12=4²﹣2² ， 20=6²﹣4² ，因此4，12，20都是“神秘数”

(1)、28和2012这两个数是“神秘数”吗？为什么？

(2)、设两个连续偶数为2k+2和2k(其中k取非负整数)，由这两个连续偶数构造的神秘数是4的倍数吗？为什么？

(3)、两个连续奇数的平方差(k取正数)是神秘数吗？为什么？

查看试题解析
14. 在课后服务课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b，宽为α的长方形，并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．

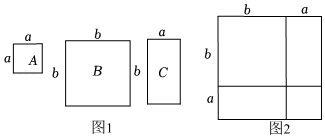(1)、根据图2，写出一个我们熟悉的数学公式．

(2)、根据（1）中的数学公式，解决如下问题：
①已知：a+b＝7，a²+b²＝25，求ab的值．
②如果一个长方形的长和宽分别为（8-x）和（x-2），且（8-x）²+（x-2）²＝20，求这个长方形的面积．

查看试题解析
15. 【发现问题】数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助我们更容易理解数学问题．现有图1中的A，B，C三种卡片若干，用这些卡片可以拼成各式各样的图形，根据这些图形的面积的不同表示可以将一些多项式因式分解．

例：用1张A卡片，2张B卡片，1张C卡片拼成如图2的图形，用两种方法表示该图形的面积，可以得到等式 $a^{2} + 2 a b + b^{2} = {(a + b)}^{2}$ ，这种把一个多项式化成几个整式的积的形式，叫做因式分解．

(1)、【小试牛刀】
请把表示图3面积的多项式因式分解（直接写出等式即可）．

(2)、【自主探索】
请利用图1的卡片，将多项式 $2 a^{2} + 5 a b + 3 b^{2}$ 因式分解，并画出图形．

(3)、【拓展迁移】
事实上，拼图不仅限于平面图形，利用立体图形的体积也可以将一些多项式因式分解．请你用此方法从体积角度简要说明如何把 $a^{3} + 4 a^{2} b + 3 a b^{2}$ 进行因式分解并写出因式分解结果．

查看试题解析

【培优卷】2024年浙教版数学七年级下册4.3用乘法公式分解因式 同步练习

一、选择题

二、填空题

三、解答题

【培优卷】2024年浙教版数学七年级下册4.3用乘法公式分解因式同步练习