2024年北师大版数学七(下)期中专项复习8 变量之间的关系
试卷更新日期:2024-03-28 类型:复习试卷
一、选择题
-
1. 苹果熟了,从树上落下来.下面可以大致刻画出苹果下落过程中(即落地前)的速度变化情况的图象是( )A、
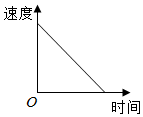 B、
B、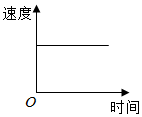 C、
C、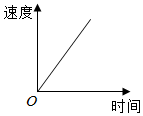 D、
D、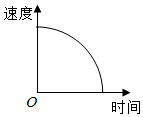 2. 弹簧挂上物体后伸长,已知一弹簧的长度与所挂物体的质量之间的关系如表:下列说法错误的是( )
2. 弹簧挂上物体后伸长,已知一弹簧的长度与所挂物体的质量之间的关系如表:下列说法错误的是( )物体的质量
弹簧的长度
A、在没挂物体时,弹簧的长度为 B、弹簧的长度随物体的质量的变化而变化,物体的质量是因变量,弹簧的长度是自变量 C、在弹簧能承受的范围内,所挂物体的质量每增加 , 弹簧的长度就增加 D、在弹簧能承受的范围内,当物体的质量为时,弹簧的长度为3. “百日长跑”是一项非常有益身心的体育活动,体育老师一声令下,小雅立即开始慢慢加速,途中一直保持匀速,最后米时奋力冲刺跑完全程,下列最符合小雅跑步时的速度单位:米分与时间单位:分之间的大致图象的是( )A、 B、
B、 C、
C、 D、
D、 4. 某人要在规定时间内加工100个零件,则工作效率与时间之间的关系中,下列说法正确的是( )A、100和都是常量 B、数100和都是常量 C、和都是变量 D、数100和都是常量5. 下表列出了一次实验的统计数据,表示皮球从高处落下时,弹跳高度b与下落高度d的关系,试问下面哪个式子能表示这种关系( )
4. 某人要在规定时间内加工100个零件,则工作效率与时间之间的关系中,下列说法正确的是( )A、100和都是常量 B、数100和都是常量 C、和都是变量 D、数100和都是常量5. 下表列出了一次实验的统计数据,表示皮球从高处落下时,弹跳高度b与下落高度d的关系,试问下面哪个式子能表示这种关系( )d/cm
50
80
100
150
……
b/cm
25
40
50
75
……
A、 B、 C、 D、6. 深圳的公交车数量位列全国之首,已知某公交小巴每月的支出费用为5000元,每月的乘车人数(人)与每月利润(每月利润=每月票款收入每月支出费用)(元)的变化关系如下表所示(每位乘客的票价固定不变),以下说法不正确的是( )(人)
……
1000
2000
3000
4000
5000
……
(元)
……
-3000
-1000
1000
3000
5000
……
A、在变化过程中,自变量是每月乘车人数 B、在变化过程中,每月的利润是因变量 C、若当月乘客达到2600人时,该公交车会亏损 D、若当月乘客达到3500人时,该公交车盈利2000元7. 一支笔2元,买x支共付y元,则2和y分别是( )A、常量,常量 B、变量,变量 C、常量,变量 D、变量,常量8. 用一根10cm长的铁丝围成的长方形,现给出四个量:①长方形的长;②长方形的宽;③长方形的周长;④长方形的面积.其中是变量的有( )A、①②③ B、①②④ C、②③④ D、①②③④9. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):温度/
-20
-10
0
10
20
30
声速/
318
324
330
336
342
348
下列说法错误的是( )
A、在这个变化中,自变量是温度,因变量是声速 B、温度越高,声速越快 C、当空气温度为时,声速为 D、当温度每升高 , 声速增加10. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):温度(℃)
-20
-10
0
10
20
30
声速()
318
324
330
336
342
348
下列说法中错误的是( )
A、当空气温度为时,5s内声音可以传播 B、温度每升高 , 声速增加 C、在这个变化过程中,自变量是温度,因变量是声速 D、温度越高,声速越快二、填空题
-
11. 蜡烛高 , 点燃后平均每小时燃掉 , 则蜡烛点燃后剩余的高度与燃烧时间时)之间的关系式是 .12. 新型冠状病毒疫情复工、复产后,某商场为了刺激消费,实施薄利多销,减少库存,现将一商品在保持销售价元件不变的前提下,规定凡购买超过件者,超出的部分打折出售.若顾客购买件,应付元,则与之间的函数关系式是 .13. 某登山队从大本营出发,在向上攀登的过程中,测得所在位置的气温y(℃)与向上攀登的高度x(km)的几组对应值如表所示:
向上攀登的高度x/km
0.5
1.0
1.5
2.0
气温y/℃
2.0
-1.0
-4.0
-7.0
若每向上攀登1 km,所在位置的气温下降幅度基本一致,则向上攀登的海拔高度为2.3 km时,登山队所在位置的气温约为°C.
14. 饮食店里快餐每盒10元,买盒需付s元,则其中因变量是 .15. 学校七年级开展种植班树活动.已知一班的班树现在高80厘米,以后一年中每个月平均长高2厘米,x月后这棵树的高度为h厘米,则h与x的函数关系式为 .三、解答题
-
16. 由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”为了测定某种型号小型载客汽车的刹车性能车速不超过 , 对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速
刹车距离
请回答下列问题:
(1)、在这个变化过程中,自变量是 , 因变量是;(2)、当刹车时车速为时,刹车距离是;(3)、根据上表反映的规律写出该种型号汽车与之间的关系式:;(4)、该型号汽车在高速公路上发生了一次交通事故,现场测得刹车距离为 , 推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶?相关法规:道路交通安全法第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过每小时公里
17. 中国联通在某地的资费标准为包月186元时,超出部分国内拨打0.36元/分,由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准
时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的表达式是什么?
(3)如果打电话超出25分钟,需付多少电话费?
(4)某次打电话的费用超出部分是54元,那么小明的爸爸打电话超出几分钟?
四、综合题
-
18. 一辆汽车油箱内有油升,从某地出发,每行驶千米,耗油升,如果设油箱内剩油量为升 , 行驶路程为千米 , 则随的变化而变化(1)、在上述变化过程中,自变量是;因变量是 .(2)、用表格表示汽车从出发地行驶千米、千米、千米、千米时的剩油量.
请将表格补充完整:
行驶路程千米
油箱内剩油量升
(3)、试写出与的关系式 .(4)、这辆汽车行驶千米时剩油多少升?汽车剩油升时,行驶了多少千米?19. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值:所挂物体的质量
0
1
2
3
4
5
…
弹簧的长度
18
20
22
24
26
28
…
(1)、不挂物体时,弹簧的长度为;(2)、当所挂物体的质量为时,弹簧的长度为多少?20. 根据心理学家研究发现,学生对一个新概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系(其中0≤x≤30)提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)、上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、根据表格中的数据,提出概念所用时间是多少时,学生的接受能力最强?(3)、学生对一个新概念的接受能力在什么时间段内逐渐增强?在什么时间段内逐渐减弱?21. 已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系:底面半径x(cm)
1.6
2.0
2.4
2.8
3.2
3.6
4.0
用铝量y(cm3)
6.9
6.0
5.6
5.5
5.7
6.0
6.5
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、当易拉罐底面半径为2.4cm时,易拉罐需要的用铝量是多少?(3)、根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由.(4)、粗略说一说易拉罐底面半径对所需铝质量的影响.22. 下表是某公共电话亭打长途电话的几次收费记录:时间x(分)
1
2
3
4
5
6
7
电话费y(元)
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)、上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?(2)、丽丽打了5分钟电话,那么电话费需付多少元?(3)、请写出y 与x之间的关系式.