【北师大版·数学】2024年中考二轮复习之特殊平行四边形
试卷更新日期:2024-03-28 类型:二轮复习
一、选择题
-
1. 如图,在平行四边形中, , , 将线段水平向右平移a个单位长度得到线段 , 若四边形为菱形时,则a的值为( )
 A、1 B、2 C、3 D、42. 如图,在矩形ABCD中,点E,F,G,H分别是边AD,AB,BC,CD的中点,连接EF,FG,CH和HE.若AD=2AB,则下列结论正确的是( )
A、1 B、2 C、3 D、42. 如图,在矩形ABCD中,点E,F,G,H分别是边AD,AB,BC,CD的中点,连接EF,FG,CH和HE.若AD=2AB,则下列结论正确的是( )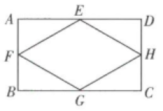 A、EF=AB B、EF=AB C、EF=AB D、EF=AB3. 任意一条线段EF的垂直平分线的尺规作图痕迹如图所示,若连接EH,HF,FG,GE,则下列结论中,不一定正确的是 ( )
A、EF=AB B、EF=AB C、EF=AB D、EF=AB3. 任意一条线段EF的垂直平分线的尺规作图痕迹如图所示,若连接EH,HF,FG,GE,则下列结论中,不一定正确的是 ( ) A、△EGF为等腰三角形 B、△EGH为等边三角形 C、四边形EGFH为菱形 D、△EHF为等腰三角形4. 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
A、△EGF为等腰三角形 B、△EGH为等边三角形 C、四边形EGFH为菱形 D、△EHF为等腰三角形4. 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4) 中正确的有( ) A、4个 B、3个 C、2个 D、1个5. 如图,已知在正方形 中,对角线 与 相交于点 , , 分别是 与 的平分线, 的延长线与 相交于点 ,则下列结论:① ;② ;③ ;④ .其中正确的结论是( )
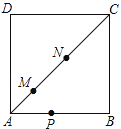
A、4个 B、3个 C、2个 D、1个5. 如图,已知在正方形 中,对角线 与 相交于点 , , 分别是 与 的平分线, 的延长线与 相交于点 ,则下列结论:① ;② ;③ ;④ .其中正确的结论是( ) A、①② B、③④ C、①②③ D、①②③④6. 如图,在正方形ABCD中,M、N是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,MN=2,设AM=x,在下列关于△PMN是等腰三角形和对应P点个数的说法中,
A、①② B、③④ C、①②③ D、①②③④6. 如图,在正方形ABCD中,M、N是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,MN=2,设AM=x,在下列关于△PMN是等腰三角形和对应P点个数的说法中,①当x=0(即M、A两点重合)时,P点有6个;
②当P点有8个时,x=2 ﹣2;
③当△PMN是等边三角形时,P点有4个;
④当0<x<4 ﹣2时,P点最多有9个.
其中结论正确是( )
 A、①② B、①③ C、②③ D、③④7. 下列命题中真命题是( )A、有一组对边平行的四边形是平行四边形 B、有一个角为90°的四边形为矩形 C、(3,﹣2)关于原点的对称点为(﹣3,2) D、有两边和一角相等的两个三角形全等8. 如图,在边长4的正方形ABCD中,E是边BC的中点,将△CDE沿直线DE折叠后,点C落在点F处,再将其打开、展平,得折痕DE.连接CF、BF、EF,延长BF交AD于点G.则下列结论:①BG=DE;②CF⊥BG;③sin∠DFG= ;④S△DFG= ,其中正确的有( )
A、①② B、①③ C、②③ D、③④7. 下列命题中真命题是( )A、有一组对边平行的四边形是平行四边形 B、有一个角为90°的四边形为矩形 C、(3,﹣2)关于原点的对称点为(﹣3,2) D、有两边和一角相等的两个三角形全等8. 如图,在边长4的正方形ABCD中,E是边BC的中点,将△CDE沿直线DE折叠后,点C落在点F处,再将其打开、展平,得折痕DE.连接CF、BF、EF,延长BF交AD于点G.则下列结论:①BG=DE;②CF⊥BG;③sin∠DFG= ;④S△DFG= ,其中正确的有( ) A、1个 B、2个 C、3个 D、4个9. 下列说法中正确的是( )A、8的立方根是2 B、函数y= 的自变量x的取值范围是x>1 C、同位角相等 D、两条对角线互相垂直的四边形是菱形10. 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
A、1个 B、2个 C、3个 D、4个9. 下列说法中正确的是( )A、8的立方根是2 B、函数y= 的自变量x的取值范围是x>1 C、同位角相等 D、两条对角线互相垂直的四边形是菱形10. 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( ) A、4.8 B、5 C、6 D、7.2
A、4.8 B、5 C、6 D、7.2二、填空题
-
11. 如图,在矩形ABCD中,∠AOB=60°,AB=5,则BD的长为。
 12. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是.
12. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是.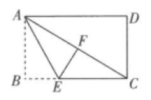 13. 菱形两条对角线长为8cm和6cm,则菱形面积为cm2 .14. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是 .
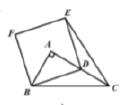
13. 菱形两条对角线长为8cm和6cm,则菱形面积为cm2 .14. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是 .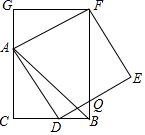 15. 如图, 中, , ,点 在边 上运动(不与点 , 重合),以 为边作正方形 ,使点 在正方形 内,连接 ,则下列结论:
15. 如图, 中, , ,点 在边 上运动(不与点 , 重合),以 为边作正方形 ,使点 在正方形 内,连接 ,则下列结论:① ;②当 时, ;
③点 到直线 的距离为 ;④ 面积的最大值是 .
其中正确的结论是 . (填写所有正确结论的序号)
三、作图题
-
16. 如图, 中, .(1)、作点 关于 的对称点 ;(要求:尺规作图,不写作法,保留作图痕迹)
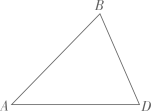 (2)、在(1)所作的图中,连接 , ,连接 ,交 于点 .
(2)、在(1)所作的图中,连接 , ,连接 ,交 于点 .①求证:四边形 是菱形;
②取 的中点 ,连接 ,若 , ,求点 到 的距离.
四、解答题
-
17. 如图,在Rt△ABC中,∠ACB=90°,D为AB中点,BE∥CD,CE∥AB.试判断四边形BDCE的形状,并证明你的结论.
 18. 如图,四边形ABCD是正方形,△CBE是等边三角形,求∠AEB的度数.
18. 如图,四边形ABCD是正方形,△CBE是等边三角形,求∠AEB的度数. 19. 已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
19. 已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.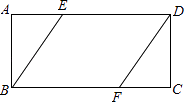
五、综合题
-
20. 如图,线段AD是△ABC的角平分线.
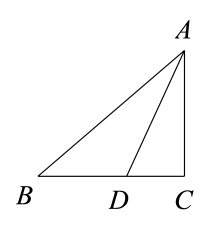 (1)、尺规作图:作线段AD的垂直平分线分别交AB,AC于点E,F:(保留痕迹,不写作法)(2)、在(1)所作的图中,连接DE,DF,求证:四边形AEDF是菱形.21. 如图
(1)、尺规作图:作线段AD的垂直平分线分别交AB,AC于点E,F:(保留痕迹,不写作法)(2)、在(1)所作的图中,连接DE,DF,求证:四边形AEDF是菱形.21. 如图 (1)、如图1,已知四边形ABCD是矩形,对角线AC,BD相交于点O,AE∥BD,DE∥AC,则四边形AODE是何种特殊四边形?(请直接写出)(2)、如图2,已知四边形ABCD是菱形,DF∥AC,CF∥DB,求证:四边形DOCF是矩形。22. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.连接OE.
(1)、如图1,已知四边形ABCD是矩形,对角线AC,BD相交于点O,AE∥BD,DE∥AC,则四边形AODE是何种特殊四边形?(请直接写出)(2)、如图2,已知四边形ABCD是菱形,DF∥AC,CF∥DB,求证:四边形DOCF是矩形。22. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.连接OE.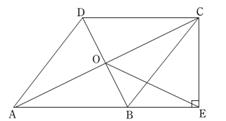 (1)、求证:四边形ABCD是菱形;(2)、若AB= .OE=2,求线段CE的长.23. 如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2 ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)、求证:四边形ABCD是菱形;(2)、若AB= .OE=2,求线段CE的长.23. 如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2 ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF. (1)、填空:点B的坐标为;(2)、是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)、①求证: = ;
(1)、填空:点B的坐标为;(2)、是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)、①求证: = ;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
-