【北师大版·数学】2024年中考二轮复习之一元二次方程

试卷更新日期：2024-03-28 类型：二轮复习

进入出卷网下载

一、选择题

1. 关于 $x$ 的一元二次方程 $x^{2} - m x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

查看试题解析
2. 对于实数 a，b，定义运算“#”如下：a#b＝a²－ab，如：3#2＝3²－3×2＝3，则方程（x＋1）#3＝2的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
3. 一元二次方程 $x^{2} + 2 x - 99 = 0$ 变形正确的是（）

A、 $(x + 1)^{2} = 100$ B、 $(x - 1)^{2} = 100$ C、 $(x + 2)^{2} = 100$ D、 $(x - 2)^{2} = 100$

查看试题解析
4. 下列一元二次方程中，有实数根的是（）

A、x²-2x+2=0 B、x²+4x+5=0 C、4x-2x²=0 D、6x²=4x-1

查看试题解析
5. 某厂家1~5月份的口罩产量统计如图所示，设从2月份到4月份，该厂家口罩产量的平均月增长率为x，则根据题意可列方程为（）

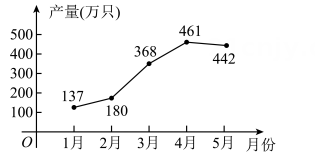A、180（1-x）²=461 B、180（1+x）²=461 C、368（1-x）²=442 D、368（1+x）²=442

查看试题解析
6. 疫情期间居民为了减少外出时间，更愿意使用 $APP$ 在线上买菜，某买菜 $APP$ 今年一月份新进册用户为200万，三月份新注册用户为338万，则二、三两个月新注册用户每月平均增长率是（）

A、10% B、15% C、23% D、30%

查看试题解析
7. 关于x的一元二次方程 $x^{2} - (k - 1) x - k + 2 = 0$ 有两个实数根 $x_{1}, x_{2}$ ， $(x_{1} - x_{2} + 2) (x_{1} - x_{2} - 2) + 2 x_{1} x_{2}$ $= - 3$ ，则k的值（）

A、0或2 B、-2或2 C、-2 D、2

查看试题解析
8. 已知 $x_{1}$ 、 $x_{2}$ 是一元二次方程 $x^{2} - 2 x = 0$ 的两个实数根，下列结论错误的是（）

A、 $x_{1} \neq x_{2}$ B、 $x_{1}^{2} - 2 x_{1} = 0$ C、 $x_{1} + x_{2} = 2$ D、 $x_{1} \cdot x_{2} = 2$

查看试题解析
9. 用公式法解方程4y²=12y+3，得到（）

A、y= $\frac{- 3 \pm \sqrt{6}}{2}$ B、y= $\frac{3 \pm \sqrt{6}}{2}$ C、y= $\frac{3 \pm 2 \sqrt{3}}{2}$ D、y= $\frac{- 3 \pm 2 \sqrt{3}}{2}$

查看试题解析
10. 我们解一元二次方程3x²﹣6x=0时，可以运用因式分解法，将此方程化为3x（x﹣2）=0，从而得到两个一元一次方程：3x=0或x﹣2=0，进而得到原方程的解为x₁=0，x₂=2．这种解法体现的数学思想是（　　）

A、转化思想 B、函数思想 C、数形结合思想 D、公理化思想

查看试题解析

二、填空题

11. 若菱形的两条对角线分别是方程x²-14x+48=0的两个实数根，则菱形的边长为．

查看试题解析
12. 某种水果的价格经过两次降价后由20元调至12元，若设该水果平均每次降价的百分率为x，则可列方程为.

查看试题解析
13. 如图，在一块长12m、宽8m的矩形空地上，修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分栽种花草，且栽种花草的面积为77m².设道路的宽为x m，则根据题意，可列方程为.

查看试题解析
14. 已知一元二次方程 $x^{2} + 6 x + m = 0$ 有两个相等的实数根，则m的值为．

查看试题解析
15. 已知关于x的一元二次方程x²﹣2（1﹣m）x+m²=0的两实数根为x₁ ， x₂ ，则y=x₁+x₂+2x₁x₂的最小值为．

查看试题解析

三、解答题

16. 我叫小白，你知道吗，2014年底南水北调中期工程开始运行，“南水”进京了，但是北京仍是特大型缺水城市，人均水资源量不到全国平均水平的 $\frac{1}{20}$ ．你了解吗，家庭中的冲水马桶是“大户”，用水量大约占家庭用水量的36%左右，两年前，我家每个月都要冲掉约3000升水．近两年来，我家使用新型冲水马桶，同时注意各种方法节水，现在我家全年用水量只有64000升，请你帮我算算，我家这两年用水的年平均下降率是多少？

查看试题解析
17. 某项绿化工程中有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56平方米，两块绿地之间及周边留有宽度相等的人行通道（如图所示），则人行通道的宽度是多少米？

查看试题解析

四、综合题

18. 已知代数式 $A = (\frac{m^{2}}{m - 2} - \frac{2 m}{m - 2}) + (m - 3) (2 m + 1)$ ．

(1)、化简A；

(2)、若m是方程 $x^{2} - 2 x = 0$ 的根，求A的值．

查看试题解析
19.

(1)、解不等式组 ${\begin{cases} 2 x + 5 \leq 3 (x + 2) 18 ， ① \\ \frac{x - 1}{2} < \frac{x}{3} ， ② \end{cases}$ 并把它的解集表示在数轴上.

(2)、下面是小颖同学解一元二次方程的过程，请认真阅读并完成相应任务.
解方程：2x²-3x-5=0
解：2x²-3x-5=0
X²- $\frac{3}{2}$ x= $\frac{5}{2}$ ………………………………………………第一步
X²- $\frac{3}{2}$ x+（ $\frac{3}{4}$ ）²= $\frac{5}{2}$ +（ $\frac{3}{4}$ ）²……………………………第二步
（x- $\frac{3}{4}$ ）²⁼ $\frac{49}{16}$ …………………………………………………………第三步
x- $\frac{3}{4}$ = $\pm$ $\frac{7}{4}$ …………………………………………………第四步
x- $\frac{3}{4}$ = $\frac{7}{4}$ ，或x- $\frac{3}{4}$ =- $\frac{7}{4}$ …………………………………………………第五步
x₁= $\frac{5}{2}$ ， x₂=-1………………………………………………………第六步
任务一：
解方程过程中第二步变形的依据是.
任务二：
请你用“公式法”解该方程.
解方程：2x²-3x-5=0

查看试题解析
20. 某服装店自2018年以来，销售成衣数量在稳健地上涨，2018年全年售出10000件成衣，2020年全年售出14400件成衣．

(1)、求该服装店2018年到2020年成衣销售量的年平均增长率；

(2)、若服装店售出成衣数量还将保持相同的年平均增长率，请你预算2022年该服装店售出成衣将达到多少件?

查看试题解析
21. 学海书店购一批故事书进行销售，其进价为每本40元，如果按每本故事书50元进行出售，每月可以售出500本故事书，后来经过市场调查发现，若每本故事书涨价1元，则故事书的销量每月减少20本．

(1)、若学海书店要保证每月销售此种故事书盈利6000元，同时又要使购书者得到实惠，则每本故事书需涨价多少元？

(2)、若使该故事书的月销量不低于300本，则每本故事书的售价应不高于多少元？

查看试题解析
22. 春节期间，佛山连锁超市派调查小组调查某种商品的销售情况，下面是调查后小李与其他两位成员交流的情况．
小李：“该商品的进价为50元/件．”

成员甲：“当定价为60元/件时，平均每天可售出800件．”

成员乙：“若售价每提高5元，则平均每天少售出100件．”

根据他们的对话，完成下列问题：

(1)、若售价定为65元/件时，平均每天可售出件；

(2)、若超市希望该商品平均每天能盈利12000元，且尽可能扩大销售量，则该商品应该怎样定价？

查看试题解析