【北师大版·数学】2024年中考二轮复习之统计与概率

试卷更新日期：2024-03-28 类型：二轮复习

进入出卷网下载

一、选择题

1. 同时掷两枚质地均匀的骰子，则两枚骰子向上的点数之和为7的概率是（）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
2. 某校举行以“激情五月，唱响青春”为主题的演讲比赛．决赛阶段只剩下甲、乙、丙、丁四名同学，则甲、乙同学获得前两名的概率是（ )

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
3. 某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习，每门课程被选中的可能性相等，小明恰好选中“烹饪”的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
4. 在一个不透明的袋子中装有黑、白两种颜色的球，这些球除颜色外完全相同，其中白球有5个，黑球有x个。从袋子中随机摸出一个球，记下颜色后，放回袋子中并摇匀。重复这一操作，经过大量重复试验发现摸出白球的频率稳定在0.25附近，则x的值为（）

A、5 B、10 C、15 D、20

查看试题解析
5. 为了庆祝中国共产党成立100周年，某校举办了党史知识竞赛活动，在获得一等奖的学生中，有3名女学生，1名男学生，则从这4名学生中随机抽取2名学生，恰好抽到2名女学生的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 将一枚飞镖投掷到如图所示的正六边形镖盘上（每次飞镖均落在镖盘上，且落在镖盘的任何一个点的机会都相等），飞镖落在阴影区域的概率为（　　）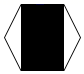

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{5}$

查看试题解析
7. 下列说法正确的是（）

A、哥哥的身高比弟弟高是必然事件 B、今年中秋节有雨是不确定事件 C、随机抛一枚均匀的硬币两次，都是正面朝上是不可能事件 D、“彩票中奖的概率为 $\frac{1}{5}$ ”表示买5张彩票肯定会中奖

查看试题解析
8. 某种商品原价是100元，经两次降价后的价格是90元．设平均每次降价的百分率为x，可列方程为（　　）

A、100x（1﹣2x）=90 B、100（1+2x）=90 C、100（1﹣x）²=90 D、100（1+x）²=90

查看试题解析
9. 下列说法正确的是（）

A、为了解人造卫星的设备零件的质量情况，选择抽样调查 B、方差是刻画数据波动程度的量 C、购买一张体育彩票必中奖，是不可能事件 D、掷一枚质地均匀的硬币一次，正面朝上的概率为1

查看试题解析
10. 在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球，从中任意摸出一个球，则摸出白球的概率是（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{5}$ C、 $\frac{1}{2}$ D、 $\frac{3}{5}$

查看试题解析

二、填空题

11. 小明从《红星照耀中国》，《红岩》，《长征》，《钢铁是怎样炼成的》四本书中随机挑选一本，其中拿到《红星照耀中国》这本书的概率为．

查看试题解析
12. 有背面完全相同，正面写有“十九届六中全会”字样的卡片n张，“元宇宙”字样的卡片4张，现正面朝下放置在桌面上，将其混合后，从中随机抽取一张，若抽中“十九届六中全会”字样的卡片的概率为 $\frac{4}{5}$ ，则 $n =$ ．

查看试题解析
13. 现有四张正面分别标有数字-3，-2，1，2的不透明卡片，它们除数字外其余完全相同，将他们背面朝上洗均匀后，随机抽取两张，记上面的数字分别为m，n，则使得一次函数 $y = 2 x + m + n$ 的图象不经过第二象限的概率为．

查看试题解析
14. 如图是一个正六边形的飞镖游戏板，顺次连接三个不相邻的顶点将正六边形分成4个区域。向该游戏板投掷飞镖一次（假设飞镖落在游戏板上，且落在游戏板上的位置是随机的），则飞镖落在阴影区域的概率是.

查看试题解析
15. 经过人民路十字路口红绿灯处的两辆汽车，可能直行，也可能左转，如果这两辆车直行和左转的可能性大小相同，则至少有一辆向左转的概率是.

查看试题解析

三、解答题

16. 甲、乙两位同学相约打乒乓球．

(1)、有款式完全相同的4个乒乓球拍 $($ 分别记为 $A$ ， $B$ ， $C$ ， $D)$ ，若甲先从中随机选取1个，乙再从余下的球拍中随机选取1个，求乙选中球拍C的概率；

(2)、双方约定：两人各投掷一枚质地均匀的硬币，如果两枚硬币全部正面向上或全部反面向上，那么甲先发球，否则乙先发球 $.$ 这个约定是否公平？为什么？

查看试题解析
17. 某中学为了解本校中考体育情况，随机抽取了部分学生的体育成绩进行统计分析，发现最低分为 45 分，且成绩为45分的学生占抽查人数的10%，现将抽查结果绘制成了如下不完整的折线统计图，请根据图中信息，回答下列问题：

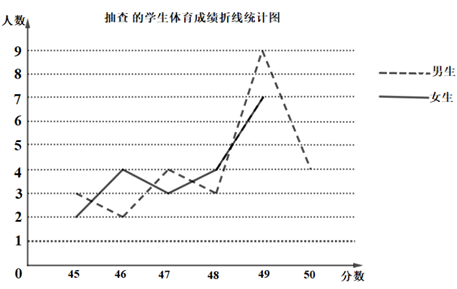(1)、此次抽查的学生人数为人，抽查的学生体育考试成绩的中位数是分，抽查的女生体育考试成绩的平均数是分；

(2)、补全折线统计图；

(3)、为了今后中考体育取得更好的成绩，学校决定分别从成绩为50分的生和女生中各选一名参加“经验座谈会”，若成绩为50分的男、女生中各有两名体育特长生，请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率．

查看试题解析
18. 某中学初三（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如下的两幅不完整的统计图(如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：

(1)、初三（1）班的学生人数为，并把条形统计图补充完整；

(2)、扇形统计图中m= ， n= ，表示“足球”的扇形的圆心角是度；

(3)、排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．

查看试题解析

四、综合题

19. 为落实中小学课后服务工作的要求，某校开设了四门校本课程供学生选择：A（合唱社团）、B（陶艺社团）、C（数独社团）、D（硬笔书法），七年级共有120名学生选择了C课程．为了解选择C课程学生的学习情况，张老师从这120名学生中随机抽取了30名学生进行测试，将他们的成绩（百分制，单位：分）分成六组，绘制成频数分布直方图．

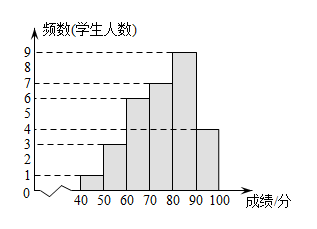(1)、 $80 ～ 90$ 分这组的数据为：81、89、84、84、84、86、85、88、83，则这组数据的中位数是分、众数是分；

(2)、根据题中信息，可以估算七年级选择C课程的学生成绩在 $70 ～ 90$ 分的人数是人；

(3)、七年级每名学生必须选两门不同的课程，小明和小华在选课程的过程中，第一门都选了课程C．他俩决定随机选择第二门课程，请用列表法或树状图的方法求他俩同时选到课程A或课程B的概率．

查看试题解析
20. 从2021年秋季开学以来，全国各地中小学都开始实行了“双减政策”．为了解家长们对“双减政策”的了解情况，从某校1200名家长中随机抽取部分家长进行问卷调查，调直评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．

(1)、本次抽取家长共有人，扇形图中“基本了解”所占扇形的圆心角是；

(2)、估计此校“非常了解”和“了解较多”的家长共有多少人?

(3)、学校计划从“了解较少”的家长中抽取1位初一学生家长，1位初二学生家长，2位初三学生家长参加培训，若从这4位家长中随机选取两人作为代表，请通过列表或面树状图的方法求所选出的两位家长既有初一家长，又有初二家长的概率．

查看试题解析

21. 某中学抽取了40名学生参加“平均每周课外阅读时间”的调查，由调查结果绘制了如下不完整的频数分布表和扇形统计图.

组别	时间/小时	频数/人数
A组	$0 \leq t < 1$	2
B组	$1 \leq t < 2$	m
C组	$2 \leq t < 3$	10
D组	$3 \leq t < 4$	12
E组	$4 \leq t < 5$	7
F组	$t \geq 5$	4

频数分布表

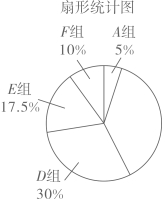
请根据图表中的信息解答下列问题：

(1)、求频数分布表中m的值；

(2)、求B组，C组在扇形统计图中分别对应扇形的圆心角度数，并补全扇形统计图；

(3)、已知F组的学生中，只有1名男生，其余都是女生，用列举法求以下事件的概率：从F组中随机选取2名学生，恰好都是女生。

查看试题解析

22. 为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为 $A$ 、 $B$ 、 $C$ 、 $D$ 四个等级，绘制如下不完整的统计图表，如题图表所示，根据图表信息解答下列问题：
成绩等级频数分布表

成绩等级

频数

A

24

B

10

C

x

D

2

合计

y

成绩等级扇形统计图

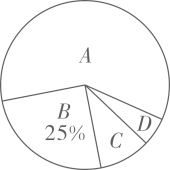(1)、x= ， y= ，扇形图中表示 $C$ 的圆心角的度数为度；

(2)、甲、乙、丙是 $A$ 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率.

查看试题解析

成绩等级	频数
A	24
B	10
C	x
D	2
合计	y