北师大版数学中考仿真模拟试题(一)
试卷更新日期:2024-03-28 类型:中考模拟
一、选择题(每题4分,共40分)
-
1. 杭州奥体中心体育场又称“大莲花”,里面有80800个座位.数据80800用科学记数法表示为( )
 A、 B、 C、 D、2. 一个立体图形的三视图如图所示,则该立体图形是( )
A、 B、 C、 D、2. 一个立体图形的三视图如图所示,则该立体图形是( )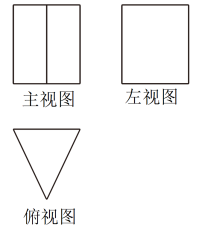 A、圆柱 B、圆锥 C、长方体 D、三棱柱3. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( )
A、圆柱 B、圆锥 C、长方体 D、三棱柱3. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( ) A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为4. 下列计算结果正确的是( )A、 B、 C、 D、5. 如图,直线 , 是直角三角形, , 点C在直线n上.若 , 则的度数是( )
A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为4. 下列计算结果正确的是( )A、 B、 C、 D、5. 如图,直线 , 是直角三角形, , 点C在直线n上.若 , 则的度数是( ) A、60° B、50° C、45° D、40°6. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , , 则内部的格点个数是( )A、266 B、270 C、271 D、2857. 4月23日是世界读书日,学校举行“快乐阅读,健康成长”读书活动.小明随机调查了本校七年级30名同学近4个月内每人阅读课外书的数量,数据如下表所示:
A、60° B、50° C、45° D、40°6. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , , 则内部的格点个数是( )A、266 B、270 C、271 D、2857. 4月23日是世界读书日,学校举行“快乐阅读,健康成长”读书活动.小明随机调查了本校七年级30名同学近4个月内每人阅读课外书的数量,数据如下表所示:人数
6
7
10
7
课外书数量(本)
6
7
9
12
则阅读课外书数量的中位数和众数分别是( )
A、8,9 B、10,9 C、7,12 D、9,98. 如图,一次函数的图象与反比例函数的图象交于点 , 则不等式的解是( ) A、或 B、或 C、或 D、或9. 如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A、或 B、或 C、或 D、或9. 如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )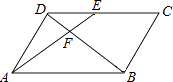 A、2:5 B、2:3 C、3:5 D、3:210. 甲、乙两台机器运输某种货物,已知乙比甲每小时多运60kg,甲运输500kg所用的时间与乙运输800kg所用的时间相等,求甲、乙两台机器每小时分别运输多少千克货物,设甲每小时运输xkg货物,则可列方程为( )A、 B、 C、 D、
A、2:5 B、2:3 C、3:5 D、3:210. 甲、乙两台机器运输某种货物,已知乙比甲每小时多运60kg,甲运输500kg所用的时间与乙运输800kg所用的时间相等,求甲、乙两台机器每小时分别运输多少千克货物,设甲每小时运输xkg货物,则可列方程为( )A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 分解因式: .12. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 .
 13. 如图,在正方形中, , 点 , 分别在边 , 上,与相交于点 , 若 , 则的长为 .
13. 如图,在正方形中, , 点 , 分别在边 , 上,与相交于点 , 若 , 则的长为 .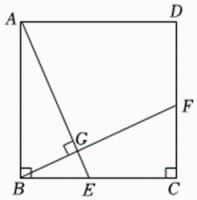 14. 已知一元二次方程的两个实数根为 , 若 , 则实数 .15. 德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年5月在此举办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加.甲、乙两名选手同时参加了往返(单程)的业余组比赛,如果全程保持匀速,甲、乙之间的距离s()与甲所用的时间(h)之间的函数关系如图所示,那么当甲到达终点时,乙距离终点 .
14. 已知一元二次方程的两个实数根为 , 若 , 则实数 .15. 德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年5月在此举办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加.甲、乙两名选手同时参加了往返(单程)的业余组比赛,如果全程保持匀速,甲、乙之间的距离s()与甲所用的时间(h)之间的函数关系如图所示,那么当甲到达终点时,乙距离终点 . 16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
三、解答题(共9题,共86分)
-
17.(1)、计算:;(2)、解不等式组: .18. 今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且 , , 靠背 , 支架 , 扶手的一部分 . 这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据: , , )
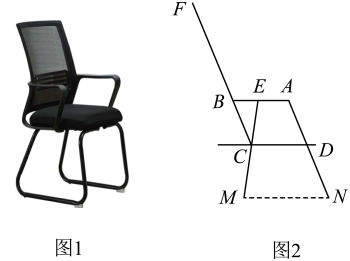 19. 如图,在中,点E , F分别在 , 的延长线上,且 , 连接与交于点M , 连接 , .
19. 如图,在中,点E , F分别在 , 的延长线上,且 , 连接与交于点M , 连接 , .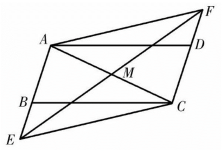 (1)、求证:;(2)、若 , , 求四边形的周长.20. 某景区旅游商店以元的价格采购一款旅游食品加工后出售,销售价格不低于元 , 不高于元 , 经市场调查发现每天的销售量与销售价格(元)之间的函数关系如图所示.
(1)、求证:;(2)、若 , , 求四边形的周长.20. 某景区旅游商店以元的价格采购一款旅游食品加工后出售,销售价格不低于元 , 不高于元 , 经市场调查发现每天的销售量与销售价格(元)之间的函数关系如图所示. (1)、求关于的函数表达式:(2)、当销售价格定为多少时,该商店销售这款食品每天获得的销售利润最大?最大销售利润是多少?【销售利润=(销售价格一采购价格)×销售量】21. 为提高学生的安全意识,某学校组织学生参加了“安全知识答题”活动该校随机抽取部分学生答题成绩进行统计,将成绩分为四个等级:优秀 , 良好 , 一般 , 不合格 , 并根据结果绘制成如图所示的两幅不完整的统计图.
(1)、求关于的函数表达式:(2)、当销售价格定为多少时,该商店销售这款食品每天获得的销售利润最大?最大销售利润是多少?【销售利润=(销售价格一采购价格)×销售量】21. 为提高学生的安全意识,某学校组织学生参加了“安全知识答题”活动该校随机抽取部分学生答题成绩进行统计,将成绩分为四个等级:优秀 , 良好 , 一般 , 不合格 , 并根据结果绘制成如图所示的两幅不完整的统计图.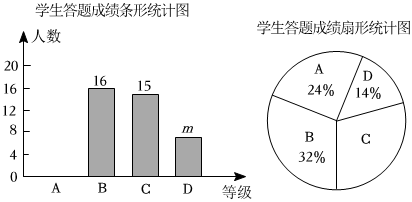
根据图中所给信息解答下列问题:
(1)、这次抽样调查共抽取人,条形统计图中的;(2)、将条形统计图补充完整,在扇形统计图中,求等所在扇形圆心角的度数;(3)、该校有名学生,估计该校学生答题成绩为等和等共有多少人;(4)、学校要从答题成绩为等且表达能力较强的甲、乙、丙、丁四名学生中,随机抽出两名学生去做“安全知识宣传员”,请用列表或画树状图的方法,求抽出的两名学生恰好是甲和丁的概率.22. 如图,已知是的直径,是的弦,点是外的一点, , 垂足为点 , 与相交于点 , 连接 , 且 , 延长交的延长线于点 .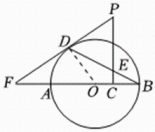 (1)、求证:是的切线;(2)、若 , , , 求的长.23. 如图,直线与双曲线相交于点 , .
(1)、求证:是的切线;(2)、若 , , , 求的长.23. 如图,直线与双曲线相交于点 , .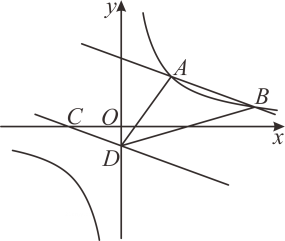 (1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.24. 正方形中,点在边 , 上运动(不与正方形顶点重合).作射线 , 将射线绕点逆时针旋转45°,交射线于点 .
(1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.24. 正方形中,点在边 , 上运动(不与正方形顶点重合).作射线 , 将射线绕点逆时针旋转45°,交射线于点 .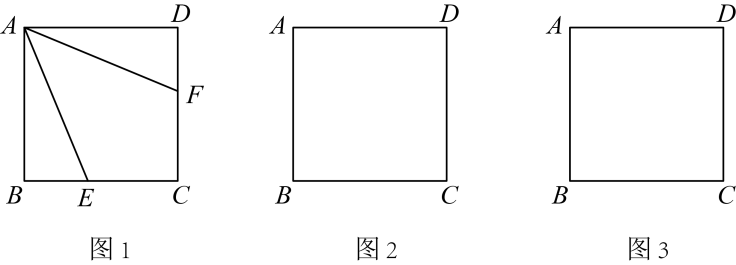 (1)、如图,点在边上, , 则图中与线段相等的线段是;(2)、过点作 , 垂足为 , 连接 , 求的度数;(3)、在(2)的条件下,当点在边延长线上且时,求的值.25. 如图,二次函数的图象与轴相交于点和点 , 交轴于点 .
(1)、如图,点在边上, , 则图中与线段相等的线段是;(2)、过点作 , 垂足为 , 连接 , 求的度数;(3)、在(2)的条件下,当点在边延长线上且时,求的值.25. 如图,二次函数的图象与轴相交于点和点 , 交轴于点 . (1)、求此二次函数的解析式;(2)、设二次函数图象的顶点为 , 对称轴与轴交于点 , 求四边形的面积(请在图1中探索);(3)、二次函数图象的对称轴上是否存在点 , 使得是以为底边的等腰三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由(请在图中探索).
(1)、求此二次函数的解析式;(2)、设二次函数图象的顶点为 , 对称轴与轴交于点 , 求四边形的面积(请在图1中探索);(3)、二次函数图象的对称轴上是否存在点 , 使得是以为底边的等腰三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由(请在图中探索).