人教版物理必修2同步练习：7.4 宇宙航行（基础巩固）

试卷更新日期：2024-03-28 类型：同步测试

进入出卷网下载

一、选择题

1. 如图所示，在地面上发射一个飞行器，进入近地圆轨道Ⅰ并绕地球运行，其发射速度 $v$ 应满足

A、 $v < 7.9 k m / s$ B、 $v = 7.9 k m / s$ C、 $v = 11.2 k m / s$ D、 $v > 11.2 k m / s$

查看试题解析
2. 嫦娥四号探测器在2019年发射升空，它是嫦娥探月工程计划中嫦娥系列的第四颗人造探月卫星。某阶段嫦娥四号绕月球做匀速圆周运动时，离月球中心的距离为r，运行周期为T，月球的半径为R，引力常量为G，根据以上信息可以求得月球的第一宇宙速度为（）

A、 $\sqrt{\frac{2 π^{2} r}{R T^{2}}}$ B、 $\sqrt{\frac{4 π^{2} r^{3}}{R T^{2}}}$ C、 $\sqrt{\frac{2 π^{2} r^{3}}{T^{2}}}$ D、 $\sqrt{\frac{4 π^{2} r^{3}}{R^{2} T^{2}}}$

查看试题解析
3. 已知月球质量与地球质量之比约为1 ： 80，月球半径与地球半径之比约为1 ： 4，则月球上的第一宇宙速度与地球上的第一宇宙速度之比最接近（）

A、9 ： 2 B、2 ： 9 C、18 ： 1 D、1 ： 18

查看试题解析
4. 2022年10月12日下午，“天宫课堂”第三课在中国空间站开讲，航天员陈冬、刘洋、蔡旭哲在离地约400km绕地球做近似圆周运动的问天实验舱进行太空投课，此次“天宫课堂”在山东省菏泽第一中学设有地面分课堂，菏泽一中的师生有幸与航天员进行互动交流，课后同学们又进行激烈讨论以下观点正确的是（　　）

A、“天宫”中宇航员由于没有受到地球引力而处于漂浮状态 B、空间站运行周期小于24小时 C、“天宫”的运行速度大于第一宇宙速度 D、载人飞船加速后可追上在同轨道上的核心舱并实施对接

查看试题解析
5. 火星探测任务“天问一号”的标识如图所示。若火星和地球绕太阳的运动均可视为匀速圆周运动，火星公转轨道半径与地球公转轨道半径之比为3∶2，则火星与地球绕太阳运动的（）

A、轨道周长之比为2∶3 B、线速度大小之比为 $\sqrt{3} ： \sqrt{2}$ C、角速度大小之比为 $2 \sqrt{2} ： 3 \sqrt{3}$ D、向心加速度大小之比为9∶4

查看试题解析
6. 中国空间站工程“巡天”望远镜（简称CSST）将于2024年前后投入运行，CSST以“天宫”空间站为太空母港，日常工作时与空间站共轨独立飞行且与空间站保持适当距离，在需要补给或者维修升级时，主动与“天宫”交会对接，停靠太空母港。已知地球半径为R，空间站轨道半径与地球半径的比值为k，地球表面的重力加速度大小为g，则CSST日常工作时的速度大小为（）

A、 $\sqrt{k g R}$ B、 $\sqrt{\frac{g R}{k}}$ C、 $\sqrt{\frac{g}{k^{2} R}}$ D、 $\sqrt{\frac{g}{k^{3} R}}$

查看试题解析
7. 北斗卫星导航系统（BDS）是我国自行研制的全球卫星导航系统。如图所示是北斗导航系统中部分卫星的轨道示意图，已知a、b、c三颗卫星均做圆周运动，a是地球同步卫星，则（　　）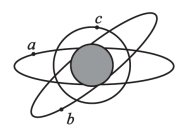

A、卫星a的角速度小于c的角速度 B、卫星a的加速度大于c的加速度 C、卫星a的运行速度大于第一宇宙速度 D、卫星b的周期小于c的周期

查看试题解析
8. 北斗卫星导航系统具有定位，授时和通信功能。北斗系统采用三种轨道卫星组网，高轨卫星更多，抗遮挡能力强，尤其低纬度地区性能特点更为明显。如图所示，卫星a、b、c沿圆形轨道绕地球运行。a是极地轨道卫星，在地球两极上空约 $1000 k m$ 处运行；b是低轨道卫星，距地球表面高度与a相等；c是地球同步卫星，则（　　）

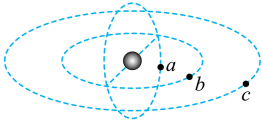A、a、b的周期比c大 B、a、b的向心力大小一定相等 C、a、b的线速度相同且比c的线速度大 D、a、b的向心加速度大小一定相等

查看试题解析
9. 如图所示，三颗人造卫星正在围绕地球做匀速固周运动，则下列有关说法中正确的是（）

A、卫星可能的轨道为 $a$ 、 $b$ 、 $c$ B、卫星可能的轨道为 $a$ 、 $c$ C、同步卫星可能的轨道为 $a$ 、 $c$ D、同步卫星可能的轨道为 $a$ 、 $b$

查看试题解析
10. 随着我国航天事业的不断发展，未来某一天，我国宇航员降落在某星球上，测得该星球表面的重力加速度为 $g^{'}$ .已知该星球半径为R，万有引力常量为G，忽略该星球自转造成的影响，则该星球的质量为（）

A、 $\frac{g^{'} R^{2}}{G}$ B、 $\frac{G R^{2}}{g^{'}}$ C、 $\frac{g^{'} R}{G}$ D、 $\frac{G R}{g^{'}}$

查看试题解析
11. 宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统。设某双星系统A、B绕其连线上的某固定点O点做匀速圆周运动，如图所示。现测得两星球球心之间的距离为L，运动周期为T，已知万有引力常量为G。若AO>OB，则（）

A、星球A的角速度一定大于星球B的角速度 B、星球A所受向心力大于星球B所受向心力 C、双星的质量一定，双星之间的距离减小，其转动周期增大 D、两星球的总质量等于 $\frac{4 π^{2} L^{3}}{G T^{2}}$

查看试题解析
12. 2012年7月26日，一个国际研究小组观测到了一组双星系统，它们绕两者连线上的某点O做匀速圆周运动。此双星系统中体积较小星体（该星体质量较小）能“吸食”另一颗体积较大星体的表面物质，达到质量转移的目的，假设在演变的过程中两者球心之间的距离保持不变，则在最初演变的过程中（）

A、它们做圆周运动的向心力保持不变且相等 B、它们做圆周运动的角速度不断变大 C、体积较大星体做圆周运动轨迹的半径变大，线速度变小 D、体积较大星体做圆周运动的轨迹半径变大，线速度也变大

查看试题解析
13. 2016年2月11日23：40左右，激光干涉引力波天文台(LIGO)首次宣布发现了引力波。它来源于距地球之外13亿光年的两个黑洞(质量分别为26个和39个太阳质量)互相绕转最后合并的过程。这一发现，证实了爱因斯坦100年前的预测，2017年诺贝尔物理学奖授予为发现引力波作出贡献的三位美国科学家。合并前两个黑洞互相绕转形成一个双星系统，关于此双星系统，只考虑双星间的相互作用，下列说法正确的是（）

A、两个黑洞绕转的线速度大小相等 B、两个黑洞的质量分别与各自绕转的线速度大小成反比 C、两个黑洞绕转的向心加速度大小相等 D、质量大的黑洞旋转半径大

查看试题解析

二、多项选择题

14. 已知地球的半径R，质量M，万有引力常量G，忽略地球的自转时地表的重力加速度g，则地球的第一宇宙速度（）

A、 $\sqrt{g R}$ B、 $\sqrt{\frac{g M}{R}}$ C、 $\sqrt{\frac{G M}{R}}$ D、 $\sqrt{\frac{R M}{g}}$

查看试题解析
15. 已知地球质量为M，半径为R，自转周期为T，地球同步卫星质量为m，引力常量为G，有关同步卫星，下列表述正确的是（）

A、该卫星距离地面的高度为 $\sqrt{\frac{G M T^{2}}{4 π^{2}}}$ B、该卫星的运行速度小于第一宇宙速度 C、该卫星运行的线速度大于地球自转的线速度 D、该卫星运行的向心加速度小于地球表面的重力加速度

查看试题解析
16. “天问一号”火星探测器被火星捕获后，经过一系列变轨进入如图所示的椭圆停泊轨道，为着陆火星做准备。P点为椭圆的近火点，Q点为远火点，关于探测器在停泊轨道上的运动（忽略其他天体的影响），下列说法正确的是（）

A、探测器的机械能守恒火星 B、探测器经过P点时的速度最大 C、探测器经过Q点时的加速度最小 D、探测器经过Q点时做“离心运动”

查看试题解析
17. 如图所示， $a$ 、 $b$ 两颗卫星分别绕地球做圆轨道运动和椭圆轨道运动， $P$ 、 $Q$ 两点分别为 $b$ 卫星椭圆轨道的近地点、远地点。则（）

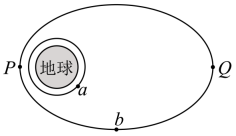A、 $a$ 卫星的运行周期可能为1小时 B、 $b$ 卫星从 $Q$ 点到 $P$ 的过程中，速度变化越来越快 C、 $a b$ 两颗卫星受到地球的引力大小有时可能相等 D、卫星 $a$ 、 $b$ 与地心的连线在相同的时间内所扫过的面积相同

查看试题解析
18. 地球同步通讯卫星相对地面是静止的，则目前尚在运行的所有地球同步通讯卫星相同的是（）

A、加速度大小 B、速率 C、动能 D、轨道

查看试题解析
19. 冥王星与其附近的另一星体卡戎可视为双星系统，质量比约为 $7 ： 1$ ，同时绕它们连线上某点O做匀速圆周运动，由此可知，冥王星绕O点运动的（）

A、轨道半径约为卡戎的 $\frac{1}{7}$ B、角速度大小约为卡戎的 $\frac{1}{7}$ C、线速度大小约为卡戎的 $\frac{1}{7}$ D、向心力大小约为卡戎的7倍

查看试题解析
20. 2018年11月，我国以“一箭双星”方式成功发射了第四十二、四十三颗北斗导航卫星，北斗系统开始提供全球服务。这两颗卫星的轨道介于近地轨道和地球同步轨道之间，属于中圆轨道。用1、2、3分别代表近地、中圆和地球同步三颗轨道卫星，关于它们运动的线速度v、角速度ω、加速度a及周期T，下列结论中正确的有（）

A、v₁＞v₂＞v₃ B、ω₁＜ω₂＜ω₃ C、a₁＞a₂＞a₃ D、T₁＜T₂＜T₃

查看试题解析
21. 双星系统由两颗恒星组成，两恒星在相互引力作用下，分别围绕其连线上某一点做周期相同的匀速圆周运动．某双星质量分别为m₁、m₂ ，做圆周运动的轨道半径分别为R₁、R₂ ，周期为T，则下列正确的是（）

A、两星质量一定相等 B、两星质量之和为m₁+m₂＝ $\frac{4 π^{2} {(R_{1} + R_{2})}^{3}}{G T^{2}}$ C、两星质量之比为 $\frac{m_{1}}{m_{2}}$ ＝ $\frac{R_{1}}{R_{2}}$ D、两星质量之比为 $\frac{m_{1}}{m_{2}}$ ＝ $\frac{R_{2}}{R_{1}}$

查看试题解析

三、非选择题

22. “玉兔号”月球车与月球表面的第一次接触实现了中国人“奔月”的伟大梦想。“玉兔号”月球车在月球表面做了一个自由下落试验，测得物体从静止自由下落h高度的时间为t ，已知月球半径为R ，引力常量为G。求：

(1)、月球的质量；

(2)、月球的第一宇宙速度。

查看试题解析
23. 某中子星的质量大约与太阳的质量相等，为 $2 \times 1 0^{30} k g$ ，但是它的半径才不过10km，(已知引力常量为 $G = 6.67 \times 1 0^{- 11} N m^{2} / k g^{2}$ ， $\sqrt{1.3} = 1.1 ， \sqrt{13} = 3.6$ )求：

(1)、此中子星表面的自由落体加速度.

(2)、此中子星的第一宇宙速度.

查看试题解析
24. 神舟号载人飞船火箭发射前，在飞船舱内用一测力计测质量为m物体的重力，测力计示数为 $T_{0}$ ；载人飞船随火箭竖直向上匀加速升空的过程中，当飞船离地面高为h时宇航员观察到测力计的示数为T。已知地球半径为R，万有引力常量为G，忽略地球自转的影响。求：

(1)、地球的质量；

(2)、地球的第一宇宙速度；

(3)、火箭匀加速上升的加速度大小。

查看试题解析
25. 2021年2月10日19时52分，我国首次火星探测任务“天问一号”探测器实施近火捕获制动，成功实现环绕火星运动，成为我国第一颗人造火星卫星。在“天问一号”环绕火星做匀速圆周运动时，周期为T ，轨道半径为r。已知火星的半径为R ，引力常量为G ，不考虑火星的自转。

(1)、“天问一号”环绕火星运动的角速度ω ，线速度的大小v；

(2)、火星的质量M。

查看试题解析
26. 两个星球组成双星，它们在相互之间的万有引力作用下，绕连线上某点做周期相同的匀速圆周运动．现测得两星中心距离为R，其运动周期为T，求两星的总质量．

查看试题解析
27. 双星系统一般都远离其他天体，由两颗距离较近的星体组成，在它们之间万有引力的相互作用下，绕中心连线上的某点做周期相同的匀速圆周运动。已知某双星系统中两颗星之间的距离为 r，运行周期为 T，引力常量为 G，求两颗星的质量之和。

查看试题解析
28. 太阳系以外存在着许多恒星与行星组成的双星系统 $.$ 它们运行的原理可以理解为：质量为M的恒星和质量为m的行星 $(M > m)$ ，在它们之间的万有引力作用下有规则地运动着 $.$ 如图所示，我们可认为行星在以某一定点C为中心、半径为a的圆周上做匀速圆周运动 $($ 图中没有表示出恒星 $) .$ 设万有引力常量为G，恒星和行星的大小可忽略不计．

(1)、求恒星与C点间的距离．

(2)、计算恒星的运行速率．

查看试题解析