人教版物理必修2同步练习：6.3 向心加速度（优生加练）

试卷更新日期：2024-03-27 类型：同步测试

进入出卷网下载

一、选择题

1. 空间站中完全失重状态下的有趣现象有时也会给航天员带来麻烦。在一些科幻作品中将空间站设计成如图所示的环形连接体，通过绕中心旋转来制造“人造重力”效果，航天员可以正常站立，就好像有“重力”使他与接触面相互挤压。下列关于这个环形空间站的说法正确的是（）

A、“人造重力”的方向指向环的中心 B、空间站的环半径越大，要制造与地表一样的重力转动的角速度越大 C、环形空间站转动越快，相邻舱体间的拉力越大 D、空间站中沿半径方向越往外，“人造重力加速度”越小

查看试题解析
2. 辘轳是古代庭院汲水的重要机械。如图，井架上装有可用手柄摇转的辘轳，辘轳上缠绕绳索，绳索一湍系水桶，摇转手柄，使水桶起落，提取井水。 $P$ 是辘轳边缘上的一质点， $Q$ 是手柄上的一质点，当手柄以恒定的角速度转动时（　　）

A、 $P$ 的线速度大于 $Q$ 的线速度 B、 $P$ 的向心加速小于 $Q$ 的向心加速度 C、辘轳对 $P$ 的作用力大小和方向都不变 D、辘轳对 $P$ 的作用力大小不变、方向变化

查看试题解析
3. 如图，两个质量相同的小球a、b，用长度不等的细线拴在同一点并在同一水平面内做匀速圆周运动。下列说法正确的是（）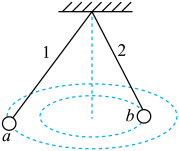

A、小球a的线速度小 B、两个小球的向心加速度大小相等 C、两个小球的角速度相等 D、细线2的张力大于细线1的张力

查看试题解析
4. 细绳拴着一个质量为m的小球，小球用固定在墙上的水平轻质弹簧支撑，平衡时细绳与竖直方向的夹角为53°，如图所示，已知重力加速度为g，cos53°=0.6，sin53°=0.8，那么剪断弹簧瞬间，小球的加速度大小为（　　）

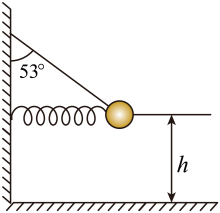A、 $\frac{3}{5} g$ B、 $\frac{4}{5} g$ C、 $\frac{4}{3} g$ D、 $\frac{5}{3} g$

查看试题解析
5. 如图所示，一个内壁光滑的圆锥筒的轴线垂直于水平面，圆锥筒固定不动，两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动，则下列说法正确的是（）

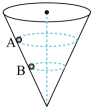A、球A的向心力大于球B的向心力 B、球A的角速度小于球B的角速度 C、球A的线速度小于球B的线速度 D、球A对筒壁的压力大于球B对筒壁的压力

查看试题解析

二、多项选择题

6. 如图所示，一细线两端固定在竖直轴上，光滑的圆环穿过细线，在水平面内绕竖直轴上的O点做匀速圆周运动，细线的上部分1与竖直轴的夹角为 $α$ ，下部分2与竖直轴的夹角为 $β$ ，重力加速度g取 $10 {m/s}^{2}$ ，下列说法正确的是（）

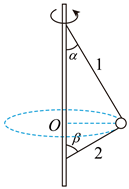A、细线的上部分1与下部分2对圆环的拉力大小不相等 B、夹角 $α$ 一定小于夹角 $β$ C、若 $α = 37 °$ 、 $β = 53 °$ （ $\sin 37 ° = 0.6$ ， $\cos 37 ° = 0.8$ ），则圆环的加速度大小为 ${12m/s}^{2}$ D、若 $α = 37 °$ 、 $β = 53 °$ ，圆环到O点的距离为0.7m，则圆环的周期为 $\frac{π}{5} s$

查看试题解析
7. 如图为用于超重耐力训练的离心机。航天员需要在高速旋转的座舱内完成超重耐力训练。这种训练的目的是为了锻炼航天员在承受巨大过载的情况下仍能保持清醒，并能进行正确操作。离心机拥有长18m的巨型旋转臂，在训练中产生8g的向心加速度，航天员的质量为70kg，可视为质点， $g = 10 m / s^{2}$ ，则下列说法正确的是（）

A、离心机旋转的角速度为 $\frac{2 \sqrt{10}}{3} rad/s$ B、离心机旋转的角速度为 $\frac{40}{9} rad/s$ C、座椅对航天员的作用力约为5600N D、座椅对航天员的作用力约为5644N

查看试题解析
8. 2021年3月15日13时29分，嫦娥五号轨道器在地面飞控人员精确控制下成功被日地—拉格朗 $L_{1}$ 点捕获，这也是我到首颗进入日地 $L_{1}$ 点探测轨道的航天器。日地 $L_{1}$ 点位于太阳与地球的连线之间，这是地球与太阳之间的引力“动平衡点”、理想状态的“日地—拉格朗日点”是只在太阳和地球对人造卫星引力作用下（忽略其它星体引力）。使人造卫星围绕太阳运行的周期与地球围绕太阳运行的周期相同的点。其中两个“日地—拉格朗日点” $L_{1}$ 和 $L_{2}$ 在日地连线上， $L_{1}$ 在地球轨道内侧， $L_{2}$ 在地球轨道外侧，如图所示，下列说法中正确的是（）

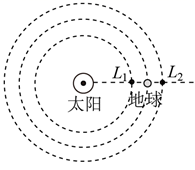A、人造卫星在 $L_{1}$ 处绕太阳运动的线速度小于地球公转的线速度 B、人造卫星在 $L_{1}$ 处绕太阳运动的角速度大于地球公转的角速度 C、人造卫星在 $L_{1}$ 处绕太阳运动的加速度小于地球公转的加速度 D、同一人造卫星所受太阳和地球万有引力的合力在 $L_{1}$ 处大于在 $L_{2}$ 处

查看试题解析
9. 和谐号动车经过一段弯道时，显示屏上显示的速率是216km/h。某乘客利用智能手机自带的指南针正在进行定位，他发现“指南针”的指针在5s内匀速转过了9°。则在此5s时间内，动车（　　）

A、转过的角度 $Δ θ = 9 rad$ B、转弯半径为 $\frac{6000}{π} m$ C、角速度为 $\frac{π}{100} rad/s$ D、向心加速度约为 $11 {m/s}^{2}$

查看试题解析
10. 小球质量为m，用长为L的轻质细线悬挂在O点，在O点的正下方 $\frac{L}{2}$ 处有一光滑钉子P，把细线沿水平方向拉直，如图所示，无初速度地释放小球，当细线碰到钉子的瞬间，设线没有断裂，则下列说法正确的是（　　）

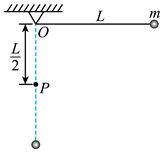A、小球的角速度突然增大 B、小球的线速度突然增大 C、小球的向心加速度突然增大 D、小球对悬线的拉力突然减小

查看试题解析
11. 以前在偏远的山区，人们通过转动辘轱用水桶从水井里向上提水。其模型可简化为：一个可绕圆心轴线转动的圆柱体上缠绕一根轻质细绳，圆柱体半径为R。质量为m的小物体P固定在细线末端，如图所示。现在把P由静止释放，物体P以加速度 $a_{0}$ 做匀加速运动，重力加速度为g，下列说法正确的是（）

A、圆柱体转动的角速度与时间成正比增加 B、圆柱体边缘上一点的向心加速度与时间成正比增加 C、在P下降距离L时，圆柱体转动的角速度大小为 $\frac{\sqrt{2 a_{0} L}}{R}$ D、在P下降距离L时，圆柱体边缘上一点的向心加速度大小为 $\frac{a_{0} L}{R}$

查看试题解析
12. 关于向心加速度，下列说法中正确的是（）

A、向心加速度越大，物体速度方向改变的就越快 B、做曲线运动的物体，一定存在向心加速度 C、由向心加速度 $a_{n} = \frac{v^{2}}{r}$ 可知，向心加速度一定与轨道半径成反比 D、物体做变速圆周运动时，向心加速度的大小不能用 $a_{n} = \frac{v^{2}}{r}$ 来计算

查看试题解析
13. 汽车后备厢盖一般都配有可伸缩的液压杆，如图甲所示，其示意图如图乙所示，可伸缩液压杆上端固定于后盖上A点，下端固定于箱内O'点，B也为后盖上一点。后盖可绕过O点的固定铰链转动。在合上后备厢盖的过程中（）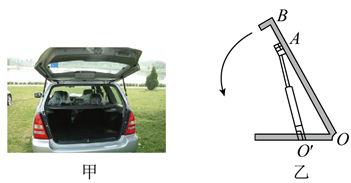

A、A点相对O'点做圆周运动 B、A点与B点相对于O点转动的线速度大小相等 C、A点与B点相对于O点转动的角速度大小相等 D、A点相对于O点转动的向心加速度小于B点相对于O点转动的向心加速度

查看试题解析
14. 如下图所示，一球体绕轴O₁O₂以角速度ω旋转，A，B为球体上两点，下列说法正确的是（）

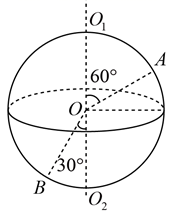A、A，B具有相等的角速度 B、A，B两点的向心加速度方向都指向球心 C、由a=ω²r知，A，B两点具有大小相等的向心加速度 D、由a=ω²r知，A的向心加速度大于B的向心加速度

查看试题解析
15. 质量均为m的小球A、B分别固定在一长为L的轻杆的中点和一端点，如图所示。当轻杆绕另一端点O在光滑水平面上做角速度为ω的匀速圆周运动时，则（）

A、处于中点的小球A的线速度为 $L ω$ B、处于中点的小球A的加速度为 $L ω^{2}$ C、处于端点的小球B所受的合外力为 $m ω^{2} L$ D、轻杆 $O A$ 段中的拉力与 $A B$ 段中的拉力之比为3：2

查看试题解析

三、非选择题

16. 如图所示为“探究小球做匀速圆周运动时的向心加速度与转速、半径的关系”的实验装置．有机玻璃支架上固定一直流电动机，电动机转轴上固定一半径为r的塑料圆盘，圆盘中心正下方用细线连接一重锤，圆盘边缘连接一轻质细绳，细绳另一端连接一个小球.实验操作如下：

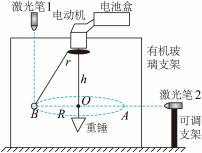
①按如图所示组装好实验器材；

②闭合电源开关，让小球做如图所示的匀速圆周运动，若不计一切阻力，当小球运动稳定时，调节水平激光笔2的高度和竖直激光笔1的位置，让激光恰好照射到小球的球心(如图中B点所示)，用刻度尺测量小球做匀速圆周运动的半径R和球心到塑料圆盘的竖直高度h；

③当小球某时刻经过图中A点时开始计时，并记录为第1次，当小球第k次经过A点时，所经历的时间为t；

④切断电源，整理器材。请回答下列问题：

(1)、小球做匀速圆周运动的向心力由____提供；

A、重力 B、绳的拉力 C、绳的拉力的水平分力 D、重力与绳的拉力的合力

(2)、若电动机的转速增大，激光笔1应 (选填“左移”或“右移”) ；

(3)、小球做匀速圆周运动的向心加速度大小为(用R 、 t 、 k 和π 表示) 。

查看试题解析
17. 为验证做匀速圆周运动物体的向心加速度与其角速度、轨道半径间的定量关系： $a = ω^{2} r$ ，某同学设计了如图所示的实验装置。其中 $A B$ 是固定在竖直转轴 $O O^{'}$ 上的水平凹槽，A端固定的压力传感器可测出小钢球对其压力的大小， $B$ 端固定一宽度为 $d$ 的挡光片，光电门可测量挡光片每一次的挡光时间。

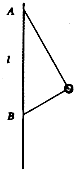
实验步骤：

①测出挡光片与转轴的距离为 $L$ ；

②将小钢球紧靠传感器放置在凹槽上，测出此时小钢球球心与转轴的距离为 $r$ ；

③使凹槽 $A B$ 绕转轴 $O O^{'}$ 匀速转动；

④记录下此时压力传感器示数 $F$ 和挡光时间 $Δ t$ 。

(1)、小钢球转动的角速度 $ω =$ （用 $L 、 d 、 Δ t$ 表示）；

(2)、若忽略小钢球所受摩擦，则要测量小钢球加速度，还需要测出，若该物理量用字母 $x$ 表示，则在误差允许范围内，本实验需验证的关系式为（用 $L 、 d 、 Δ t 、 F 、 r 、 x$ 表示）。

查看试题解析
18. “求知”兴趣小组研究“向心加速度与运动半径的关系”。

(1)、经过一系列对比实验，得出结论：若角速度 $ω$ 相同，向心加速度大小a与运动半径r成；若线速度大小v相同，向心加速度大小a与运动半径r成。（均选填“正比”或“反比”）

(2)、下列关于向心加速度的说法正确的是____。

A、向心加速度表示做圆周运动的物体速率改变的快慢 B、向心加速度表示角速度变化的快慢 C、做匀速圆周运动的物体的向心加速度不变 D、向心加速度描述的是线速度方向变化的快慢

查看试题解析
19. 有一种叫“飞椅”的游乐项目如图。长为 $L$ 的钢绳一端系着座椅，另一端固定在半径为 $r$ 的水平转盘边缘。转盘可绕穿过其中心的竖直轴转动。当转盘以角速度 $ω$ 匀速转动时，钢绳与转轴在同一竖直平面内，与竖直方向的夹角为 $θ$ 。不计钢绳的重力。

(1)、座椅的转动的速度是多大；

(2)、写出转盘转动的角速度 $ω$ 与夹角 $θ$ 的关系；

(3)、已知人和座椅的总质量 $M = 80 k g$ ，钢绳长 $L = 4 m$ ，水平转盘半径 $r = 4 m$ ，当钢绳受到的力为 $800 \sqrt{2} N$ 时，转盘转动的角速度 $ω$ 为多大。

查看试题解析
20. 张华同学用如图所示装置测量玩具电动汽车前轮的转速和前轮边缘的向心加速度的大小，已知永久磁铁每经过传感器一次，传感器就输出一个电压脉冲，计数器显示的数字就增加1.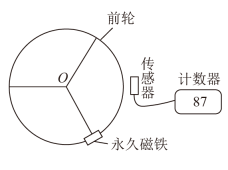

(1)、已有玩具电动汽车、电源、传感器、计数器、永久磁铁等仪器，要完成测量，还需要的测量仪器是、。

(2)、把永久磁铁粘在前轮的边缘让前轮匀速转动，从计数器第一次显示数字开始计时，当计数器上显示的数字为N时，记录的时间为t，测量出前轮的半径为r。玩具电动汽车前轮转速表达式n=、前轮边缘向心加速度大小的表达式a=。（用字母N、t、r表示）

查看试题解析
21. 某同学做“验证向心力与线速度关系”的实验。装置如图所示，一轻质细线上端固定在拉力传感器上，下端悬挂一小钢球。已知钢球直径为d，钢球静止时刚好位于光电门中央。主要实验步骤如下：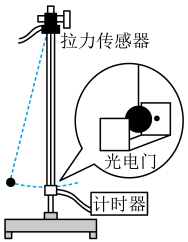

①将钢球悬挂静止不动，此时拉力传感器示数为 $F_{1}$ ，用米尺量出线长L；

②将钢球拉到适当的高度处释放，光电门计时器测出钢球的遮光时间为t，拉力传感器示数的最大值为 $F_{2}$ ；

已知当地的重力加速度大小为g，请用上述测得的物理量表示：

(1)、钢球经过光电门时的线速度表达式 $v =$ ，向心力表达式 $F_{向} =$ ；

(2)、钢球经过光电门时所受合力的表达式 $F_{合} =$ ；
若在实验误差允许的范围内 $F_{向} = F_{合}$ ，则验证了向心力与线速度的关系。

查看试题解析
22. 为验证匀速圆周运动的向心加速度与角速度、轨道半径间的定量关系，某同学设计了如图甲所示的实验装置。其中AB是固定在竖直转轴 $O O$ 上的水平平台，A端固定的压力传感器可测出小物体对其压力的大小，B端固定一宽度为d的挡光片，光电门可测量挡光片每一次的挡光时间。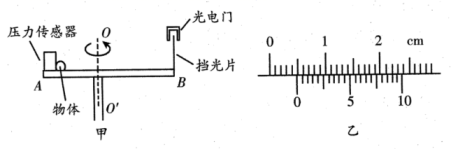
实验步骤如下：
①测出挡光片与转轴间的距离L；
②将小物体紧靠传感器放置在平台上，测出小物体中心与转轴的距离r；
③使平台AB绕转轴 $O O$ 匀速转动；
④记录压力传感器的示数F和对应的挡光时间 $Δ t$ ；
⑤保持小物体质量和距离r不变，多次改变转动角速度，记录压力传感器示数F和对应的挡光时间 $Δ t$ 。

(1)、小物体转动的角速度 $ω =$ （用L、d、 $Δ t$ 表示）；若某次实验中挡光片的宽度如图乙所示，其读数为mm；

(2)、要验证小物体的向心加速度与角速度、轨道半径间的定量关系，还需要测出小物体的质量m，则在误差允许范围内，本实验需验证的关系式为（用所测物理量的符号表示）。

查看试题解析
23. 如图所示，一个小球绕圆心O做匀速圆周运动。已知圆周半径为r，小球运动的角速度为 $ω$ ，则它运动的线速度大小为，向心加速度大小为。

查看试题解析
24. 天花板上悬挂一轻质弹簧，测得其原长为 $r$ ，当其下端固定一可视为质点、质量为 $m$ 的小球静止后弹簧的长度为 $l_{1}$ 。现将轻弹簧和小球转移至光滑水平面，轻弹簧的一端固定在水平面内的竖直转轴 $O$ 点上，现使小球获得一初速度，最后小球和弹簧一起绕转轴 $O$ 做匀速圆周运动，测得小球做匀速圆周运动的周期为 $T$ ，已知弹簧始终处于弹性限度内，重力加速度大小为 $g$ 。求：

(1)、小球做匀速圆周运动时弹簧的形变量；

(2)、小球运动过程中的向心加速度大小。

查看试题解析
25. “嫦娥五号”于2020年11月24日在海南文昌发射中心成功发射，携带月壤采样于12月17日成功返回，开启了我国对月球的进一步探测工程。在此之前，科技人员反复进行了多次模拟试验以应对各种可能的异常情况。在模拟实验中月球探测器（如图）能够在自动导航系统的控制下行走，且每隔10s向地球发射一次无线电信号。探测器上还装有两套相同的使探测器获得加速度的装置（简称减速器，其中一个备用）。某次试验中探测器的自动导航系统出现故障，从而使探测器只能匀速直线前进而不能自动避开障碍物，此时地面控制人员就需要进行人工遥控操作。下表为地面操控中心显示屏上的部分数据：已知月球距地球约为r = 3.0 × 10⁵km，控制中心接收到信号到控制人员发出指令最少需要Δt = 3s时间。前方障碍物相对探测器极大，可将该情况简化为探测器正垂直驶向无限大的障碍物（如图）。
回答以下问题：

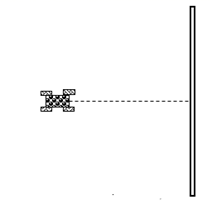
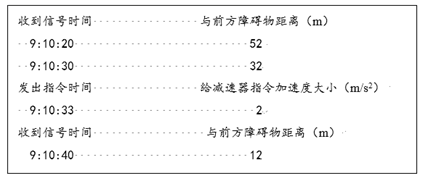(1)、通过对显示屏上的数据分析，你认为减速器是否执行了9：10：33发出的减速指令？

(2)、分析说明为避免本次碰撞，在加速度大小相同的情况下，发出哪种指令更安全？
①做匀速圆周运动②做匀减速直线运动

(3)、若你是控制中心人员，在9：10：40接收到信号后，应该怎么做？若发出指令②，给减速器设定的加速度需要满足什么条件？

查看试题解析
26. 如图所示，长为l的细线一端固定在O点，另一端拴一质量为m的小球，让小球在水平面内做角速度为 $ω$ 的匀速圆周运动，摆线与竖直方向成 $θ$ 角，求小球运动的向心加速度．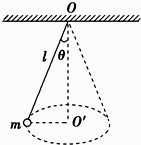

查看试题解析
27.

(1)、匀速圆周运动的速度方向不断发生变化，如图所示，经过Δt时间，线速度由v_A变为v_B ，圆周的半径为r.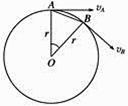

试根据加速度的定义式推导向心加速度大小的公式.

(2)、结合v=ωr推导可得向心加速度与角速度关系的表达式为：a_n=？.

(3)、有人说：根据a_n= $\frac{v^{2}}{r}$ 可知，向心加速度与半径成反比，根据a_n=ω²r可知，向心加速度与半径成正比，这是矛盾的.你认为呢？

查看试题解析
28.
某电视台正在策划的“快乐向前冲”节目的场地设施如图所示，AB为水平直轨道，上面安装有电动悬挂器，可以载人运动，下方水面上漂浮着一个半径为R铺有海绵垫的转盘，转盘轴心离平台的水平距离为L，平台边缘与转盘平面的高度差H．选手抓住悬挂器后，按动开关，在电动机的带动下从A点沿轨道做初速为零、加速度为a的匀加速直线运动．起动后2s悬挂器脱落．设人的质量为m（看作质点），人与转盘间的最大静摩擦力为μmg，重力加速度为g．

(1)、假设选手落到转盘上瞬间相对转盘速度立即变为零，为保证他落在任何位置都不会被甩下转盘，转盘的角速度ω应限制在什么范围；

(2)、若H=3.2 m，R=0.9 m，取g=10m/s² ，当a=2m/s²时选手恰好落到转盘的圆心上，求L；

(3)、若H=2.45 m，R=0.8 m，L=6m，取g=10m/s² ，选手要想成功落在转盘上，求加速度a的范围．

查看试题解析
29.
一竖直杆上相距l的A、B两点拴着一根不可伸长的轻绳，绳长1.4l，绳上套着一个光滑的小铁环，设法转动竖直杆，不让绳缠绕在杆上，而让铁环在某水平面上做匀速圆周运动，如图所示，当两段绳成直角时，求铁环转动的周期，已知重力加速度为g．

查看试题解析