人教版物理必修2同步练习：6.1 圆周运动（优生加练）

试卷更新日期：2024-03-27 类型：同步测试

进入出卷网下载

一、选择题

1. 如图是多级减速装置的示意图。每一个轮子都由大小两个轮子叠合而成，共有n个这样的轮子，用皮带逐一联系起来，设大轮的半径为R，小轮的半径为r，当第一个轮子的大轮外缘线速度大小为v₁时，第n个轮子的小轮边缘线速度大小为（设皮带不打滑）（）

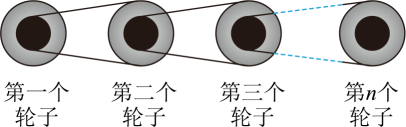A、 $\frac{r}{R} v_{1}$ B、 $\frac{R}{r} v_{1}$ C、 ${(\frac{r}{R})}^{n} v_{1}$ D、 ${(\frac{R}{r})}^{n - 1} v_{1}$

查看试题解析
2. 如图为自行车气嘴灯及其结构图，弹簧一端固定在A端，另一端拴接重物，当车轮高速旋转时，LED灯就会发光。下列说法正确的是（）

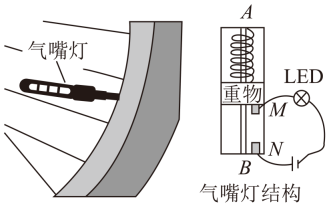A、安装时A端比B端更远离圆心 B、高速旋转时，重物由于受到离心力的作用拉伸弹簧从而使触点接触，电路导通，LED灯发光 C、增大重物质量可使LED灯在较低转速下也能发光 D、匀速行驶时，若LED灯转到最低点时能发光，则在最高点时也一定能发光

查看试题解析
3. 如图所示，完全相同的两车在水平面同心圆弧道路上转弯，甲行驶在内侧、乙行驶在外侧，它们转弯时速度大小相等，则两车在转弯时，下列说法正确的是（）

A、角速度 $ω_{甲} = ω_{乙}$ B、向心加速度a_甲>a_乙 C、地面对车的径向摩擦力f_甲＜f _乙 D、若两车转弯速度过大，则乙车更容易发生侧滑

查看试题解析
4. 如图所示，复兴号列车以速率v通过一段水平弯道，转弯半径为r，列车恰好与轨道间没有侧向压力，不计空气阻力，重力加速度为g，则下列判断正确的是（）

A、列车左右两车灯的线速度大小相等 B、弯道处的外轨略高于内轨 C、内外轨所在斜面的倾角满足 $s i n θ = \frac{v^{2}}{g r}$ D、质量为m的乘客在拐弯过程中，受到列车给他的作用力为 $m \frac{v^{2}}{r}$

查看试题解析
5. 如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω转动，盘面上离转轴距离2.5m处有一小物体与圆盘始终保持相对静止，物体与盘面间的动摩擦因数为 $\frac{\sqrt{3}}{2}$ ，（设最大静摩擦力等于滑动摩擦力），盘面与水平面的夹角为30°，g取10m/s² ，则ω的最大值是（）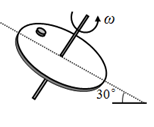

A、1.0rad/s B、0.5rad/s C、 $\sqrt{3}$ rad/s D、 $\sqrt{5}$ rad/s

查看试题解析
6. 如图所示的机械装置可以将圆周运动转化为直线上的往复运动。连杆AB、OB可绕图中A、B、O三处的转轴转动，连杆OB在竖直面内的圆周运动可通过连杆AB使滑块在水平横杆上左右滑动。已知OB杆长为L，绕O点做逆时针方向匀速转动的角速度为ω，当连杆AB与水平方向夹角为α，AB杆与OB杆的夹角为β时，滑块的水平速度大小为（）

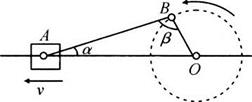A、 $\frac{ω L sin β}{sin α}$ B、 $\frac{ω L cos β}{sin α}$ C、 $\frac{ω L cos β}{cos α}$ D、 $\frac{ω L sin β}{cos α}$

查看试题解析
7. 一水平放置的圆盘绕竖直固定轴转动，在圆盘上沿半径方向开有一条宽度为2.5mm的均匀狭缝，将激光器与传感器上下对准，使二者间连线与转轴平行，分别置于圆盘的上下两侧，且可以同步地沿圆盘半径方向匀速移动，激光器连续向下发射激光束．在圆盘转动过程中，当狭缝经过激光器与传感器之间时，传感器接收到一个激光信号，并将其输入计算机，经处理后画出相应图线．图（a）为该装置示意图，图（b）为所接收的光信号随时间变化的图线，横坐标表示时间，纵坐标表示接收到的激光信号强度，图中△t₁=1.0×10^-3s，△t₂=0.8×10^-3s．根据图（b）以下分析正确的是（）

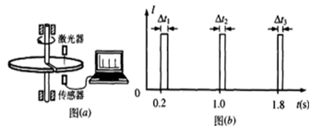A、圆盘转动角速度逐渐增大 B、圆盘转动周期逐渐增大 C、第三个激光信号的宽度 △t₃=0.6×10^-3s D、激光器和传感器沿半径向外运动

查看试题解析
8. 如图所示，用长为L的轻绳（轻绳不可伸长）连接的甲、乙两物块（均可视为质点），放置在水平圆盘上，甲、乙连线的延长线过圆盘的圆心O，甲与圆心O的距离也为L，甲、乙两物体的质量均为m，与圆盘间的动摩擦因数均为μ，物块与圆盘间的最大静摩擦力等于滑动摩擦力，甲、乙始终相对圆盘静止，则下列说法中正确的是（）

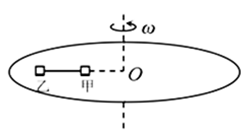A、圆盘转动的角速度最大为 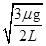B、圆盘转动的角速度最大为 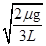C、轻绳最大弹力为 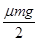D、轻绳最大弹力为μmg

查看试题解析
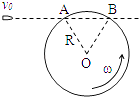
9.
子弹以初速度v₀水平向右射出，沿水平直线穿过一个正在沿逆时针方向转动的薄壁圆筒，在圆筒上只留下一个弹孔（从A位置射入，B位置射出，如图所示）．OA、OB之间的夹角θ= $\frac{π}{3}$ ，已知圆筒半径R=0.5m，子弹始终以v₀=60m/s的速度沿水平方向运动（不考虑重力的作用），则圆筒的转速可能是（）

A、20r/s B、60r/s C、100r/s D、140r/s

查看试题解析
10.
如图所示，两个啮合齿轮，小齿轮半径为10cm，大齿轮半径为20cm，大齿轮中C点离圆心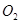的距离为10cm，A、B分别为两个齿轮边缘上的点，则A、B、C三点的（　　）

A、线速度之比为1：1：1 B、角速度之比为1：1：1 C、向心加速度之比为4：2：1 D、转动周期之比为2：1：1

查看试题解析
11. 如图所示，为一皮带传动装置，右轮的半径为r ， a是它的边缘上的一点，左侧是一轮轴，大轮的半径为4r ，小轮的半径为2r ， b点在小轮上，到小轮中心距离为r ， c点和d点分别位于小轮和大轮的边缘上，若在传动过程中，皮带不打滑，则（　　）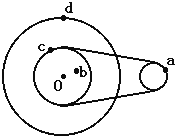

A、a点与b点线速度大小相等 B、a点与c点角速度大小相等 C、a点与d点向心加速度大小不相等 D、a、b、c、d四点，加速度最小的是b点

查看试题解析
12. 如图所示，相同材料的A、B两物块置于绕竖直轴匀速转动的水平圆盘上，B的质量是A的质量的2倍，A与转动轴的距离等于B与转动轴的距离2倍，两物块相对于圆盘静止，则两物块（　　）

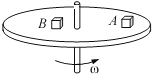A、角速度相同 B、线速度相同 C、向心加速度相同 D、若转动的角速度增大，A、B同时滑动

查看试题解析
13.
如图所示，物体P用两根长度相等不可伸长的细线系于竖直杆上，它们随杆转动，若转动角速度为ω，则下列说法错误的是（）

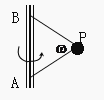A、ω只有超过某一值时，绳子AP才有拉力 B、线BP的拉力随ω的增大而增大 C、线BP的拉力一定大于线AP的拉力 D、当ω增大到一定程度时，线AP的拉力将大于BP的拉力

查看试题解析

二、多项选择题

14. 如图所示，质量分别为m和2m的A、B两个物块（可视为质点）在水平圆盘上沿直径方向放置，与转盘的动摩擦因数均为μ（可认为最大静摩擦力等于滑动摩擦力）。A离轴的距离为R ， B离轴的距离为2R ，两物块用一根细绳连在一起。A、B随圆盘以角速度 $ω$ 一起做匀速圆周运动，且与圆盘保持相对静止，下列说法正确的是（）

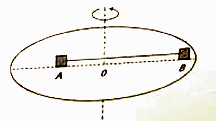A、A所受的合外力与B所受的合外力大小相等 B、B所受摩擦力方向指向圆心 C、若 $ω < \sqrt{\frac{μ g}{2 R}}$ ，细绳无张力 D、若 $ω > \sqrt{\frac{μ g}{R}}$ ，A、B两物块与圆盘发生相对滑动

查看试题解析
15. 如图所示，两物块A、B套在水平粗糙的CD杆上，并用不可伸长的轻绳连接，整个装置能绕过CD中点的轴OO'转动，已知两物块质量相等，杆CD对物块A、B的最大静摩擦力大小相等，开始时绳子处于自然长度（绳子恰好伸直但无弹力），物块A到OO'轴的距离为物块B到OO'轴距离的两倍，现让该装置从静止开始转动，使转速逐渐增大，在从绳子处于自然长度到两物块A、B即将滑动的过程中，下列说法正确的是（）

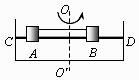A、B受到的静摩擦力一直增大 B、B受到的静摩擦力是先增大后减小 C、A受到的静摩擦力是先增大后不变 D、A受到的合外力一直在增大

查看试题解析
16. 如图所示，一位同学玩飞镖游戏．圆盘最上端有一P点，飞镖抛出时与P等高，且距离P点为L．当飞镖以初速度v₀垂直盘面瞄准P点抛出的同时，圆盘以经过盘心O点的水平轴在竖直平面内匀速转动．忽略空气阻力，重力加速度为g，若飞镖恰好击中P点，则（）

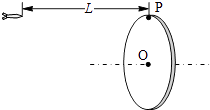A、飞镖击中P点所需的时间为 $\frac{L}{v_{0}}$ B、圆盘的半径可能为 $\frac{g L^{2}}{2 v_{0}^{2}}$ C、圆盘转动角速度的最小值为 $\frac{2 π v_{0}}{L}$ D、P点随圆盘转动的线速度可能为 $\frac{5 π g L}{4 v_{0}}$

查看试题解析

三、非选择题

17. 地面上有一个半径为R = 0.5m的圆形跑道，一平台边缘上的P点在地面上P′点的正上方，P′与跑道圆心O的距离为 $L = \sqrt{3} R$ ，如图所示，ABCD为跑道上的4个点，（其中AC为水平直径，BD是与AC垂直的直径）跑道上有一辆小车。现从P点以速度v₀= 0.5m/s水平抛出一沙袋，已知g取10m/s² ，求：

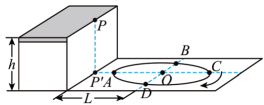(1)、若小车静止于B点时，沙袋被抛出后落入小车中，平台的高度h为多高？

(2)、若抛出沙袋的同时小车从A点顺时针出发，沿跑道做匀速圆周运动，欲使沙袋恰好能够在D处落入小车中，求小车运动的线速度v满足什么条件？

查看试题解析
18. 如图所示，区域Ⅰ内有与水平方向成 $4 5^{°}$ 角的匀强电场E₁ ，区域宽度为d₁ ，区域Ⅱ内有正交的有界匀强磁场B和匀强电场E₂ ，区域宽度为d₂ ，磁场方向垂直纸面向里，电场方向竖直向下．一质量为m、带电荷量为q的微粒在区域Ⅰ左边界的P点，由静止释放后水平向右做直线运动，进入区域Ⅱ后做匀速圆周运动，从区域Ⅱ右边界上的Q点穿出，其速度方向改变了 $6 0^{°}$ ，重力加速度为g，求：

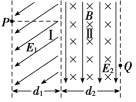(1)、区域Ⅰ和区域Ⅱ内匀强电场的电场强度E₁、E₂的大小；

(2)、区域Ⅱ内匀强磁场的磁感应强度B的大小；

(3)、微粒从P运动到Q的时间．

查看试题解析
19. 如图所示，半径 $R = 1 m$ 的水平圆盘可绕其竖直轴转动，在圆盘的边缘关于转轴对称的两点放上质量均为m的相同小物块A、B，并将它们用轻质细线连接，当圆盘静止时，保持细线伸直且恰无张力。已知物块与圆盘间的动摩擦因数 $μ = 0.4$ ，细线可承受的最大拉力 $T_{m} = 0.5 m g$ ，认为最大静摩擦力均等于滑动摩擦力，取 $g = 10 m / s^{2}$ 。现让圆盘开始转动并缓慢增大其角速度，求：

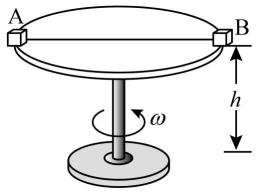(1)、细线产生弹力时圆盘的角速度 $ω_{1}$ ；

(2)、细线断裂时圆盘的角速度 $ω_{m}$ ；

(3)、已知圆盘距地面的高度 $h = \frac{15}{9} m$ ，求细线断裂后A、B落地点间的距离。

查看试题解析
20. 如图所示， $x O y$ 坐标平面内的第一、二象限内有垂直纸面向外的匀强磁场，第三、四象限内有沿 $y$ 轴负方向的匀强电场。一带电粒子自 $M$ 点以大小为 $v_{0}$ 的速度沿 $x$ 轴正方向射出，已知匀强电场的电场强度为 $E ， M$ 点的坐标为 $(- L ， - \frac{\sqrt{3} L}{2})$ ，匀强磁场的磁感应强度为 $\frac{E}{\sqrt{3} v_{0}}$ ，粒子带负电，比荷 $\frac{q}{m} = \frac{\sqrt{3} v_{0}^{2}}{E L}$ ，带电粒子的重力忽略不计，求：

(1)、带电粒子第一次经过 $x$ 轴时的横坐标和速度；

(2)、带电粒子自 $M$ 开始到第二次经过 $y$ 轴的时间；

(3)、带电粒子第 $(2 n + 1)$ 次经过 $x$ 轴时的 $x$ 坐标 $(n = 0 ， 1 ， 2 ， \dots \dots)$ 。

查看试题解析
21. 如图甲所示的空间直角坐标系Oxyz中，分界面P、荧光屏Q均与平面Oxy平行，分界面P把空间分为区域Ⅰ和区域II两部分，分界面P与平面Oxy间的距离为L，z轴与分界面P相交于 $O^{'}$ 。区域Ⅰ空间中分布着沿y轴正方向的匀强电场，区域Ⅱ空间中分布有沿x轴正方向和z轴正方向的磁场，磁感应强度大小均为 $B_{0}$ ，变化规律如图乙所示。两个电荷量均为q、质量均为m的带正电粒子A、B在y轴负半轴上的两点沿z轴正方向先后射出，经过区域Ⅰ，两粒子均打到 $O^{'}$ 点，其中粒子A到达 $O^{'}$ 点时速度大小为 $v_{0}$ ，方向与z轴正方向成 $θ = 60 °$ 角；在O点有一特殊的粒子处理器，使A、B粒子只保留垂直z方向的速度，并且同时从 $O^{'}$ 点射出，以粒子在 $O^{'}$ 点射出时的时刻为 $t = 0$ 时刻，再经过区域Ⅱ，其中粒子A刚好打到荧光屏Q上，粒子B在 $t = \frac{5 π m}{3 q B_{0}}$ 时打在荧光屏上形成一个亮点。粒子所受重力忽略不计，不考虑场的边缘效应及相对论效应，求：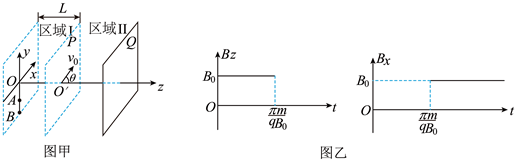

(1)、区域Ⅰ内电场强度E的大小；

(2)、分界面P与荧光屏Q之间的距离d；

(3)、A、B粒子在y轴上出发时的坐标之比 $\frac{y_{1}}{y_{2}}$ 。

查看试题解析
22. 如图所示，BC是用光滑细圆管弯成的竖直圆弧轨道，O为圆弧轨道的圆心，在圆管的末端C连接倾斜角为45°、动摩擦因数μ=0.6的足够长粗糙斜面，一质量为m=0.1kg的小球从O点正上方某处A点以v₀=2m/s水平抛出，恰好能垂直OB从B端进入细圆管，小球从进入圆管开始受到始终竖直向上的力F=1N的作用，当小球运动到圆管的末端C时作用力F立即消失，小球能平滑地冲上粗糙斜面。（g=10m/s² ， $\sqrt{2} = 1.4$ ）求：

(1)、A点与B点的竖直高度是多少？

(2)、小球在圆管中运动时对圆管的压力是多大？

(3)、小球在CD斜面上运动的最大位移是多少？

查看试题解析
23. 如图所示，一个质量为m=0. 6kg的小球，以某一初速度 $v_{0}$ 从图中P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧轨道（不计空气阻力，进入时无机械能损失）。已知圆弧半径R=0.3m，图中θ=60°，小球到达A点时的速度v=4m/s（取g=10m/s²）。试求：

(1)、小球做平抛运动的初速度 $v_{0}$ 。

(2)、判断小球能否通过圆弧最高点C。若能，求出小球到达圆弧轨道最高点C时对轨道的压力F_N。

查看试题解析
24. 动画片《熊出没》中有这样一个情节：某天熊大和熊二中了光头强设计的陷阱，被挂在了树上（如图甲），聪明的熊大想出了一个办法，让自己和熊二荡起来使绳断裂从而得救，其过程可简化如图乙所示，设悬点为O，离地高度为2L，两熊可视为质点且总质量为m，绳长为 $\frac{L}{2}$ 且保持不变，绳子能承受的最大张力为3mg，不计一切阻力，重力加速度为g，求：

(1)、设熊大和熊二刚好在向右摆到最低点时绳子刚好断裂，则他们的落地点离O点的水平距离为多少；

(2)、改变绳长，且两熊仍然在向右到最低点绳子刚好断裂，则绳长为多长时，他们的落地点离O点的水平距离最大，最大为多少；

(3)、若绳长改为L，两熊在水平面内做圆锥摆运动，如图丙，且两熊做圆锥摆运动时绳子刚好断裂，则他们落地点离O点的水平距离为多少。

查看试题解析
25. 科技馆有一套儿童喜爱的机械装置，其结构简图如下：传动带AB部分水平，其长度L=1.2m，传送带以3m/s的速度顺时针匀速转动，大皮带轮半径r=0.4m，其下端C点与圆弧轨道DEF的D点在同一水平线上，E点为圆弧轨道的最低点，圆弧EF对应的圆心角θ= $37^{°}$ 且圆弧的半径R=0.5m，F点和倾斜传送带GH的下端G点平滑连接，倾斜传送带GH长为x=4.45m，其倾角θ= $37^{°}$ 。某同学将一质量为0.5kg且可以视为质点的物块静止放在水平传送带左端A处，物块经过B点后恰能无碰撞地从D点进入圆弧轨道部分，当经过F点时，圆弧对物块支持力N=29.0N，然后物块滑上倾斜传送带GH。已知物块与所有的接触面间的动摩擦因数均为μ=0.5，重力加速度g=10m/s² ， sin $37^{°}$ =0.6，cos $37^{°}$ =0.8， $\sqrt{7.2} = 2.68$ ，求：

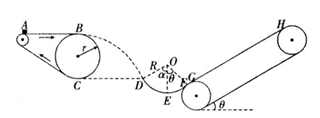(1)、物块由A到B所经历的时间；

(2)、DE弧对应的圆心角 $α$ 为多少；

(3)、若要物块能被送到H端，则倾斜传动带顺时针运转的速度最小值v_min为多少。

查看试题解析
26. 如图所示，水平转台上有一个质量为m的物块，用长为L的细绳将物块连接在转轴上，细线与竖直转轴的夹角为 $θ$ 角，此时绳中张力为零，物块与转台间动摩擦因数为 $μ (μ < \tan θ)$ ，最大静摩擦力等于滑动摩擦力物块随转台由静止开始缓慢加速转动，求

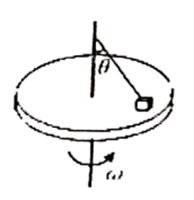(1)、至绳中出现拉力时，转台的角速度大小；

(2)、至转台对物块支持力为零时，转台对物块做的功；

(3)、设法使物体的角速度增大到 $\sqrt{\frac{3 g}{2 L \cos θ}}$ 时，物块机械能增量。

查看试题解析
27. 如图所示，半径为R的半球形陶罐固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴OO′重合，转台以一定角速度ω匀速旋转，一质量为m的小物块落入陶罐内，经过一段时间后，小物块随着陶罐一起转动且相对罐壁静止，它和O点的连线与OO′之间的夹角θ为45°。已知重力加速度大小为g，小物块与陶罐之间的最大静摩擦力大小为 $F = \frac{\sqrt{2} m g}{4}$ 。

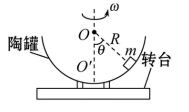(1)、若小物块受到的摩擦力恰好为零，求此时的角速度ω₀

(2)、若改变陶罐匀速旋转的角速度，而小物块一直相对陶罐静止，求陶罐旋转的角速度的最大值和最小值。

查看试题解析
28. 如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴OO′重合，转台以一定角速度ω匀速旋转，一质量为m的小物块落入陶罐内，经过一段时间后，小物块随陶罐一起转动且相对罐壁静止，它和O点的连线与OO′之间的夹角θ为45°.已知重力加速度大小为g ，小物块与陶罐之间的最大静摩擦力大小为 $F_{f} = \frac{\sqrt{2}}{4} m g$ .

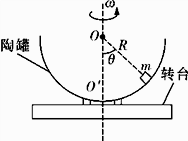(1)、若小物块受到的摩擦力恰好为零，求此时的角速度ω₀；

(2)、若小物块一直相对陶罐静止，求陶罐旋转的角速度的最大值和最小值．

查看试题解析