2024年中考数学真题改编贵州模拟试卷(一)
试卷更新日期:2024-03-26 类型:中考模拟
一、选择题
-
1. 的绝对值是( )A、 B、 C、 D、2. 下列四个几何体中,主视图为圆的是( )A、
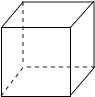 B、
B、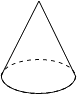 C、
C、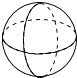 D、
D、 3. 某自动控制器的芯片,可植入2020000000粒晶体管,2020000000用科学记数法表示为( ).A、 B、 C、 D、4. 如图,已知 , , 若 , 则的度数是( )
3. 某自动控制器的芯片,可植入2020000000粒晶体管,2020000000用科学记数法表示为( ).A、 B、 C、 D、4. 如图,已知 , , 若 , 则的度数是( ) A、 B、 C、 D、5. 化简结果正确的是( )A、 B、1 C、 D、6. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )
A、 B、 C、 D、5. 化简结果正确的是( )A、 B、1 C、 D、6. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )时间/小时
7
8
9
10
人数
7
9
11
3
A、9,8 B、9,8.5 C、10,9 D、11,8.57. 如图,在中, , , 且 , 则BD长为( ) A、1 B、2 C、3 D、48. 一个布袋里装有3个红球,4个黑球,5个白球,它们除颜色外都相同,从中任意摸出一个球,则下列事件中,发生可能性最大的是( )A、摸出的是红球 B、摸出的是黑球 C、摸出的是绿球 D、摸出的是白球9.
A、1 B、2 C、3 D、48. 一个布袋里装有3个红球,4个黑球,5个白球,它们除颜色外都相同,从中任意摸出一个球,则下列事件中,发生可能性最大的是( )A、摸出的是红球 B、摸出的是黑球 C、摸出的是绿球 D、摸出的是白球9.《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?”设共有个人共同出钱买鸡,则下面所列方程正确的是( )
A、 B、 C、 D、10. 二次函数y=-2x2的图象开口方向是( )A、向下 B、向左 C、向上 D、向右11. 如图,在矩形ABCD中,∠BAC=60°,以点A为圆心,任意长为半径作圆弧分别交AB、AC于点M、N,再分别以点M、N为圆心,大于MN的长为半径作弧,两弧交于点P,作射线AP交BC于点E,若BE=1,则△AEC的面积为( ) A、1 B、2 C、 D、12. “五岳归来不看山,黄山归来不看岳”中的黄山是中国十大风景名胜唯一的山岳风光,为国家5A级旅游景区.每当雨后天晴或暮春时节,山间白云缭绕,蔚为奇观.五一假期,亚男一家从家出发自驾前往黄山游玩,经过服务区时,休息一段时间后继续驶往目的地,汽车行驶路程(千米)与汽车行驶时间(分钟)之间的函数关系如图所示.下列判断不正确的是( )
A、1 B、2 C、 D、12. “五岳归来不看山,黄山归来不看岳”中的黄山是中国十大风景名胜唯一的山岳风光,为国家5A级旅游景区.每当雨后天晴或暮春时节,山间白云缭绕,蔚为奇观.五一假期,亚男一家从家出发自驾前往黄山游玩,经过服务区时,休息一段时间后继续驶往目的地,汽车行驶路程(千米)与汽车行驶时间(分钟)之间的函数关系如图所示.下列判断不正确的是( )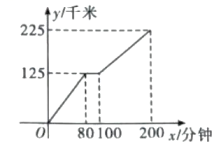 A、他们出发80分钟后到达服务区 B、他们在服务区休息了20分钟 C、亚男家距离黄山350千米 D、在服务区休息前的行驶速度比休息后快
A、他们出发80分钟后到达服务区 B、他们在服务区休息了20分钟 C、亚男家距离黄山350千米 D、在服务区休息前的行驶速度比休息后快二、填空题
-
13. 因式分解:2m2﹣2= .14. 如图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(2,),目标B 的位置为(4,),现有一个目标C的位置为(3,),且与目标B的距离为5,则目标C的位置为 .
 15. 已知关于的一元二次方程有实数根,则的取值范围是 .16. 如图,在长方形ABCD中,AD=8cm,AB=6cm,E为AD的中点,若点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在线段BC上由点B向点C运动,当△AEP与△BPQ全等时,点Q的运动速度是cm/s.
15. 已知关于的一元二次方程有实数根,则的取值范围是 .16. 如图,在长方形ABCD中,AD=8cm,AB=6cm,E为AD的中点,若点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在线段BC上由点B向点C运动,当△AEP与△BPQ全等时,点Q的运动速度是cm/s.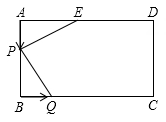
三、解答题
-
17. 计算:
18. 已知 , , 求的值。19. 近些年,新能源汽车以其清洁环保、使用成本低、高能源利用率等优点,慢慢走进人们的生活.下面是我国某区域2023年各季度新能源汽车销售量情况统计图. (1)、这个区域2023年共销售新能源汽车万辆,其中一季度销售万辆.(2)、将上面的条形统计图和扇形统计图中缺失的数据填、画完整.(3)、2023年平均每季度的增长量为(4)、结合以上信息,请你预测2024年这个区域新能源汽车的销售量可能是 ▲ 万辆.将你预测的理由写在下面.20. 小明用元买软面笔记本,小丽用元买硬面笔记本.已知每本硬面笔记本比软面笔记本贵元.(1)、设软面笔记本每本元,则小丽买硬面笔记本本;(2)、小明和小丽能买到相同数量的笔记本吗?21. 如图,在四边形ABCD中,∠BAC=∠ACD=90°, , E是CD的中点,连结 AE.
(1)、这个区域2023年共销售新能源汽车万辆,其中一季度销售万辆.(2)、将上面的条形统计图和扇形统计图中缺失的数据填、画完整.(3)、2023年平均每季度的增长量为(4)、结合以上信息,请你预测2024年这个区域新能源汽车的销售量可能是 ▲ 万辆.将你预测的理由写在下面.20. 小明用元买软面笔记本,小丽用元买硬面笔记本.已知每本硬面笔记本比软面笔记本贵元.(1)、设软面笔记本每本元,则小丽买硬面笔记本本;(2)、小明和小丽能买到相同数量的笔记本吗?21. 如图,在四边形ABCD中,∠BAC=∠ACD=90°, , E是CD的中点,连结 AE.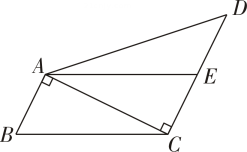 (1)、求证:四边形ABCE 是平行四边形.(2)、若AC=4,AD=4 , 求四边形 ABCE 的面积.22. 如图,直线与双曲线(k为常数,交于 , 两点,与轴、轴分别交于 , 两点,点的坐标为 .
(1)、求证:四边形ABCE 是平行四边形.(2)、若AC=4,AD=4 , 求四边形 ABCE 的面积.22. 如图,直线与双曲线(k为常数,交于 , 两点,与轴、轴分别交于 , 两点,点的坐标为 . (1)、求反比例函数的解析式.(2)、结合图象直接写出当时,的取值范围.23. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上)(参考数据: , , , )
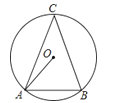
(1)、求反比例函数的解析式.(2)、结合图象直接写出当时,的取值范围.23. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上)(参考数据: , , , )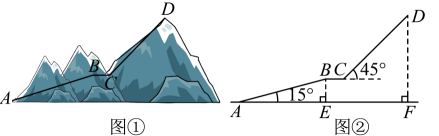 (1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).24. 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
(1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).24. 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
(3)若点C平分优弧AB,且BC2=3OA2 , 试求α的度数.
 25. 如图,隧道的截面由抛物线DEC和矩形ABCD构成,矩形的长AB为4m,宽BC为3m,以DC所在的直线为x轴,线段CD的中垂线为y轴,建立平面直角坐标系。y轴是抛物线的对称轴,最高点E到地面距离为4米.
25. 如图,隧道的截面由抛物线DEC和矩形ABCD构成,矩形的长AB为4m,宽BC为3m,以DC所在的直线为x轴,线段CD的中垂线为y轴,建立平面直角坐标系。y轴是抛物线的对称轴,最高点E到地面距离为4米.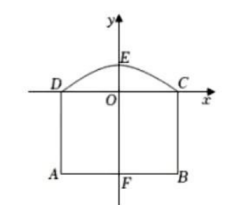 (1)、求出抛物线的解析式.(2)、在距离地面米高处,隧道的宽度是多少?(3)、如果该隧道内设单行道(只能朝一个方向行驶),现有一辆货运卡车高3.6米,宽2.4米,这辆货运卡车能否通过该隧道?通过计算说明你的结论.
(1)、求出抛物线的解析式.(2)、在距离地面米高处,隧道的宽度是多少?(3)、如果该隧道内设单行道(只能朝一个方向行驶),现有一辆货运卡车高3.6米,宽2.4米,这辆货运卡车能否通过该隧道?通过计算说明你的结论.四、实践探究题
-
26. 已知,如图①,是等边三角形, , 是线段上的动点.
 (1)、问题解决:在图①中,若 , 根据给出的已知条件,直接写出一条未知线段的长度或一个角的大小;(2)、问题探究:如图②,在(1)的条件下,以线段为边在右侧作等边 , 连接 , 猜想与的数量关系并证明;(3)、拓展延伸:如图③,以线段为边在右侧作等边 , 在点从点向点的运动过程中,猜想点的运动路径是什么?当的值最小时,点运动路径的长度?(直接写出结果)
(1)、问题解决:在图①中,若 , 根据给出的已知条件,直接写出一条未知线段的长度或一个角的大小;(2)、问题探究:如图②,在(1)的条件下,以线段为边在右侧作等边 , 连接 , 猜想与的数量关系并证明;(3)、拓展延伸:如图③,以线段为边在右侧作等边 , 在点从点向点的运动过程中,猜想点的运动路径是什么?当的值最小时,点运动路径的长度?(直接写出结果)