新疆维吾尔自治区阿克苏地区阿克苏市2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-26 类型:期末考试
一、单选题
-
1. 某几何体如图所示,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 若函数的图象经过点 , 则的值为( )A、6 B、 C、12 D、3. 二次函数图象与y轴的交点坐标是( )A、 B、 C、 D、4. 若一元二次方程的一个根为0,则k的值为( )A、 B、 C、 D、或5. 如图,和是以点O为位似中心的位似图形, , 的周长为8,则的周长为( )
2. 若函数的图象经过点 , 则的值为( )A、6 B、 C、12 D、3. 二次函数图象与y轴的交点坐标是( )A、 B、 C、 D、4. 若一元二次方程的一个根为0,则k的值为( )A、 B、 C、 D、或5. 如图,和是以点O为位似中心的位似图形, , 的周长为8,则的周长为( ) A、12 B、18 C、20 D、246. 下列命题正确的是( )A、方程没有实数根 B、两边成比例及一角对应相等的两个三角形相似 C、平分弦的直径垂直于弦 D、反比函数的图象不会与坐标轴相交7. 如图,将绕点顺时针旋转得到 , 若线段 , 则的长为( )
A、12 B、18 C、20 D、246. 下列命题正确的是( )A、方程没有实数根 B、两边成比例及一角对应相等的两个三角形相似 C、平分弦的直径垂直于弦 D、反比函数的图象不会与坐标轴相交7. 如图,将绕点顺时针旋转得到 , 若线段 , 则的长为( )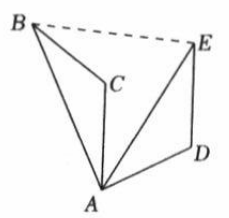 A、3 B、4 C、5 D、68. 已知二次函数(m为常数)的图象与x轴的一个交点为 , 则关于x的一元二次方程的两个实数根是( )A、 , B、 , C、 , D、 ,9. 对称轴为直线的抛物线(a , b , c为常数,且)如图所示,小明同学得出了以下结论:① , ② , ③ , ④ , ⑤(m为任意实数),⑥当时,y随x的增大而减小.其中结论正确的个数为( )
A、3 B、4 C、5 D、68. 已知二次函数(m为常数)的图象与x轴的一个交点为 , 则关于x的一元二次方程的两个实数根是( )A、 , B、 , C、 , D、 ,9. 对称轴为直线的抛物线(a , b , c为常数,且)如图所示,小明同学得出了以下结论:① , ② , ③ , ④ , ⑤(m为任意实数),⑥当时,y随x的增大而减小.其中结论正确的个数为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
10. 点与点B关于原点中心对称,则点B的坐标为 .11. 若 , 是方程的两个实数根,则代数式的值等于 .12. 夜晚小明在路灯下散步,离路灯越近,他的影子越(填“长”或“短”).13. 电路图上有四个开关和一个小灯泡,如果同时闭合中的两个开关,那么使得小灯泡发亮的概率是 .
 14. 如图,是的直径,点D , C在上,连接 , , , 如果 , 那么的度数是 .
14. 如图,是的直径,点D , C在上,连接 , , , 如果 , 那么的度数是 .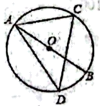 15. 如图,点在反比例函数()的图象上,且点是线段的中点,点为轴上一点,连接交反比例函数图象于点 , 连接 , 若 , , 则的值为 .
15. 如图,点在反比例函数()的图象上,且点是线段的中点,点为轴上一点,连接交反比例函数图象于点 , 连接 , 若 , , 则的值为 .
三、解答题
-
16. 解方程:(1)、(2)、17. 如图,一次函数的图象与反比例函数的图象相交于 , 两点.
 (1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足的的取值范围.18. 如图,在中,是直径,弦 , 垂足为E , 连接 , .
(1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足的的取值范围.18. 如图,在中,是直径,弦 , 垂足为E , 连接 , . (1)、求证:;(2)、若 , , 求的长度.19. 如图,一架无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为 , 无人机与旗杆的水平距离为6米,求该校的旗杆高为多少米.(结果保留根号)
(1)、求证:;(2)、若 , , 求的长度.19. 如图,一架无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为 , 无人机与旗杆的水平距离为6米,求该校的旗杆高为多少米.(结果保留根号) 20. 某校开展了学习党史的知识竞赛活动.初三年级学生的比赛成绩根据结果分为 , , , 四个等级.其等级对应的分值分别为100分~91分、90分~81分、80分~71分、70分及以下.现将初三学生的最后等级成绩分析整理绘制得到了两幅不完整的统计图,请根据图中的信息解决下面的问题.
20. 某校开展了学习党史的知识竞赛活动.初三年级学生的比赛成绩根据结果分为 , , , 四个等级.其等级对应的分值分别为100分~91分、90分~81分、80分~71分、70分及以下.现将初三学生的最后等级成绩分析整理绘制得到了两幅不完整的统计图,请根据图中的信息解决下面的问题. (1)、由图可知该校初三共名学生,比赛成绩等级为级的学生人数是人;(2)、请补全条形统计图,由图可知的值为▲ ;(3)、初三年级本次比赛获得满分的4人中有2个男生和2个女生,年级要求从这4个学生中随机选2人参加学校决赛,若每个学生被抽取的可能性相等,请用画树状图或者列表法求抽取的2人中至少有1个男生的概率.21. 春节期间,阿克苏市某商场积压了一批棉衣,现欲尽快清仓,确定降价促销.据调查发现,若每件棉衣盈利50元时,可售出50件,每件棉衣每下降1元,则可多售出2件.设每件棉衣降价x元.(1)、每件棉衣降价x元后,现在每件棉衣盈利元,可售出棉衣件(用含x的代数式表示)(2)、若要使销售该棉衣的总利润达到2800元,求x的值.(3)、当每件棉衣降价多少元时,获利最大?最大利润是多少元?22. 如图,等腰中 , 以为直径的与、的延长线分别交于点E、D,垂直于F.
(1)、由图可知该校初三共名学生,比赛成绩等级为级的学生人数是人;(2)、请补全条形统计图,由图可知的值为▲ ;(3)、初三年级本次比赛获得满分的4人中有2个男生和2个女生,年级要求从这4个学生中随机选2人参加学校决赛,若每个学生被抽取的可能性相等,请用画树状图或者列表法求抽取的2人中至少有1个男生的概率.21. 春节期间,阿克苏市某商场积压了一批棉衣,现欲尽快清仓,确定降价促销.据调查发现,若每件棉衣盈利50元时,可售出50件,每件棉衣每下降1元,则可多售出2件.设每件棉衣降价x元.(1)、每件棉衣降价x元后,现在每件棉衣盈利元,可售出棉衣件(用含x的代数式表示)(2)、若要使销售该棉衣的总利润达到2800元,求x的值.(3)、当每件棉衣降价多少元时,获利最大?最大利润是多少元?22. 如图,等腰中 , 以为直径的与、的延长线分别交于点E、D,垂直于F. (1)、求证:为的切线;(2)、若 , , 求的长.23. 在平面直角坐标系中,抛物线与x轴的交点为 , , 与y轴交于点C .
(1)、求证:为的切线;(2)、若 , , 求的长.23. 在平面直角坐标系中,抛物线与x轴的交点为 , , 与y轴交于点C . (1)、求抛物线的函数表达式;(2)、如图1,连接 , P是第二象限内抛物线上一动点,过点P作交直线AC于点G , 作轴交直线AC于点R , 求最大值以及此时点P的坐标;(3)、如图2,将抛物线沿射线AC平移个单位,得到新抛物线 , M为新抛物线对称轴上一点,N为新抛物线上一点,当以P、B、M、N为顶点的四边形是平行四边形时,请直接写出所有符合条件的N点的坐标,并把求其中一个点N的过程写出来.
(1)、求抛物线的函数表达式;(2)、如图1,连接 , P是第二象限内抛物线上一动点,过点P作交直线AC于点G , 作轴交直线AC于点R , 求最大值以及此时点P的坐标;(3)、如图2,将抛物线沿射线AC平移个单位,得到新抛物线 , M为新抛物线对称轴上一点,N为新抛物线上一点,当以P、B、M、N为顶点的四边形是平行四边形时,请直接写出所有符合条件的N点的坐标,并把求其中一个点N的过程写出来.