新疆和田地区2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-03-26 类型:期末考试
一、单选题(每小题3分,共30分)
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算中,正确的是( )A、a3+a3=2a6 B、a5﹣a3=a2 C、a2•a2=2a4 D、(a5)2=a103. 如图,AB∥CD,∠A=40°,求∠2的度数( )
2. 下列运算中,正确的是( )A、a3+a3=2a6 B、a5﹣a3=a2 C、a2•a2=2a4 D、(a5)2=a103. 如图,AB∥CD,∠A=40°,求∠2的度数( ) A、85° B、90° C、75° D、45°4. 下列四个图形中,线段BE是△ABC的高的是( )A、
A、85° B、90° C、75° D、45°4. 下列四个图形中,线段BE是△ABC的高的是( )A、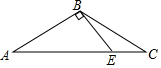 B、
B、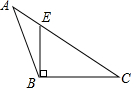 C、
C、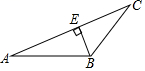 D、
D、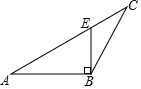 5. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
5. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.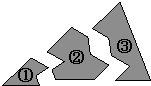 A、① B、② C、③ D、①和②6. 已知点A(a,2)与点B(3,b)关于x轴对称( )A、﹣4 B、﹣1 C、﹣2 D、47. 若9x2+kxy+4y2是一个完全平方式,则k的值为( )A、6 B、±6 C、12 D、±128. 如图,有A,B,C三个居民小区的位置成三角形,使超市到三个小区的距离相等,则超市应建在( )
A、① B、② C、③ D、①和②6. 已知点A(a,2)与点B(3,b)关于x轴对称( )A、﹣4 B、﹣1 C、﹣2 D、47. 若9x2+kxy+4y2是一个完全平方式,则k的值为( )A、6 B、±6 C、12 D、±128. 如图,有A,B,C三个居民小区的位置成三角形,使超市到三个小区的距离相等,则超市应建在( ) A、在边AC,BC两条高的交点处 B、在边AC,BC两条中线的交点处 C、在边AC,BC两条垂直平分线的交点处 D、在∠ABC,∠ACB两条角平分线的交点处9. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式( )
A、在边AC,BC两条高的交点处 B、在边AC,BC两条中线的交点处 C、在边AC,BC两条垂直平分线的交点处 D、在∠ABC,∠ACB两条角平分线的交点处9. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式( ) A、(a+2b)(a﹣b)=a2+ab﹣2b2 B、(a+b)2=a2+2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、(a﹣b)2=a2﹣2ab﹣b2 .10. 如图,在△ABC中,AD平分∠BAC,DE⊥AB,垂足为点E.若△ACD的面积为16,AC=8,则DE的长为 ( )
A、(a+2b)(a﹣b)=a2+ab﹣2b2 B、(a+b)2=a2+2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、(a﹣b)2=a2﹣2ab﹣b2 .10. 如图,在△ABC中,AD平分∠BAC,DE⊥AB,垂足为点E.若△ACD的面积为16,AC=8,则DE的长为 ( ) A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6二、填空题(每小题3分,共18分)
-
11. 化简:(12a3﹣6a2+3a)÷3a= .12. 如果分式的值为零,那么x= .13. 十二边形的内角和为 度.14. 计算(π﹣3)0+( )﹣1= .15. 若am=2,an=3,则 =16. 如图,在△ABC中,AB=AC,BC=4,△ABC的面积为20,AB的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则BM+DM的最小值为 .

三、解答题(本题7小题,共52分)
-
17. 计算:(1)、5a2•(3a3)2;(2)、分解因式:mn2﹣9m.18. 解分式方程:(1)、=;(2)、 +1.19. 先化简代数式 ,再从﹣2,2,0三个数中选一个恰当的数作为a的值代入求值.20. 如图,已知△ABC三个顶点的坐标分别为A(4,3),B(2,1),C(5,﹣1).
 (1)、画出△ABC关于y轴对称的图形△A'B'C' , 并写出A',B',C'的坐标;(2)、求出△A'B'C'的面积.21. 如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)、画出△ABC关于y轴对称的图形△A'B'C' , 并写出A',B',C'的坐标;(2)、求出△A'B'C'的面积.21. 如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF. (1)、求证:△ABC≌△DEF;(2)、若∠A=65°,∠B=82°,求∠F的度数.22. 已知:如图△ABC中AC=6cm,AB=8cm,BD平分∠ABC,CD平分∠ACB,过D作直线平行于BC,交AB,AC于E,F.
(1)、求证:△ABC≌△DEF;(2)、若∠A=65°,∠B=82°,求∠F的度数.22. 已知:如图△ABC中AC=6cm,AB=8cm,BD平分∠ABC,CD平分∠ACB,过D作直线平行于BC,交AB,AC于E,F. (1)、求证:△DFC是等腰三角形;(2)、求△AEF的周长.23. 六•一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.(1)、求A、B两种品牌服装每套进价分别为多少元?(2)、该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
(1)、求证:△DFC是等腰三角形;(2)、求△AEF的周长.23. 六•一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.(1)、求A、B两种品牌服装每套进价分别为多少元?(2)、该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?