江西省吉安市峡江县2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-26 类型：期末考试

进入出卷网下载

一、选择题（本大题共6小题，每小题3分，共18分）

1. 9的平方根是（　　）

A、±3 B、 $\pm \frac{1}{3}$ C、3 D、-3

查看试题解析
2. 下列命题中，假命题的个数有（）
①实数与数轴上的点一一对应；②无限小数就是无理数；③一个数的算术平方根是它本身，这个数是1；④三角形的一个外角大于任何一个和它不相邻的内角；⑤两条直线被第三条直线所截，同旁内角互补．

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在某中学元旦汇演中，10位评委给八年级1班比赛的成绩打分如下表：
成绩/分
94
95
96
97
98
99
评委人数
2
1
3
1
2
1
则这组成绩的众数和中位数分别是（）

A、95，95 B、96，96 C、96，95 D、96，97

查看试题解析
4. 如图，一棵大树在一次强台风中于离地面3m处折断倒下，树干顶部落在距根部4m处，这棵大树在折断前的高度为（）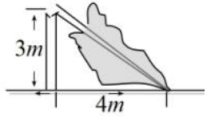

A、5米 B、7米 C、8米 D、12米

查看试题解析
5. 如图，直线 $y = x + 5$ 和直线 $y = a x + b$ 相交于点P，根据图象可知，关于x的方程 $x + 5 = a x + b$ 的解是（）

A、x＝20 B、x＝25 C、x＝－20 D、x＝－25

查看试题解析
6. 若点 $(m ， n)$ 在第二象限，则一次函数 $y = n x + m - n$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

7. 若 $\sqrt{x} = 8$ ，则 $\sqrt[3]{x} =$ ．

查看试题解析
8. 已知：a，b是两个连续的整数，且 $a < - \sqrt{10} < b$ 则 $a - b =$ ．

查看试题解析
9. 将一副直角三角板如下图放置，已知∠E＝60°，∠C＝45°， $E F ∥ B C$ ，则∠BND＝．

查看试题解析
10. 如图，一束光沿CD方向，先后经过平面镜OB、OA反射后，沿EF方向射出，已知∠A0B＝120°∠CDB＝20°，则∠AEF＝．

查看试题解析
11. 已知一组数据a，b，c的方差是2，那么另一组数据 $2 a + 1$ ， $2 b + 1$ ， $2 c + 1$ 的方差是．

查看试题解析
12. 若关于x、y的方程组 ${\begin{cases} a x + 3 y = 9 \\ 2 x + 3 y = 0 \end{cases}$ 有整数解，则正整数a的值为．

查看试题解析

三、解答题（本大题共5小题，每小题6分，共30分）

13. 计算：

(1)、 $\sqrt{12} - \sqrt{3} + 2 \sqrt{\frac{1}{3}}$

(2)、 $(2 \sqrt{2} + 3) (2 \sqrt{2} - 3) + \sqrt[3]{- 8}$

查看试题解析
14. 解方程组： ${\begin{array}{l} 2 x - y = 5 \\ 7 x - 3 y = 18 \end{array}$

查看试题解析
15. 已知：如图，∠CAE是△ABC的外角，AD∥BC且∠1＝∠2，求证：AB＝AC．

查看试题解析
16. 一只螳螂在一圆柱形松树树干的点A处，它发现在其正上方的点B处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是按如图所示的路线，绕到虫子后面吃掉它．已知树干的底面周长为20cm，A，B两点间的距离为15cm，求螳螂绕行的最短路程．

查看试题解析
17. 如图，在每个小正方形的边长均为1个单位长度的网格中，△ABC的三个顶点都在格点上，请用无刻度直尺作图，并保留作图痕迹．

(1)、在图1中，请以直线l为对称轴，画出与△ABC成轴对称的图形．

(2)、在图2中，请在直线l上找一点P，使得BP⊥AC．

查看试题解析

四、解答题（本大题共3小题，每小题8分，共24分）

18. 我国古代数学名著《九章算术》中记载：“粟米之法：粟率五十：粝米三十．今有米在十斗桶中，不知其数．满中添粟而春之，得米七斗，问故米几何？”意思为：50斗谷子能出30斗米，即出米率为 $\frac{3}{5}$ 。今有米在容量为10斗的桶中，但不知道数量是多少．再向桶中加满谷子，再春成米，共得米7斗．问原来有米多少斗？向桶中加了谷子多少斗？

查看试题解析
19. 某公司要在甲、乙两人中招聘一名职员，对两人的学历、能力、经验这三项进行了测试．各项满分均为10分，平均成绩高者被录用．图1是甲、乙测试成绩的条形统计图，

(1)、分别求出甲、乙三项平均成绩，并指出会录用谁；

(2)、若将甲、乙的三项测试成绩，按照扇形统计图（图2）各项所占之比，分别计算两人各自的综合成绩，并判断是否会改变（1）的录用结果．

查看试题解析
20. 某网络公司推出了一系列上网包月业务，其中的一项业务是100M网络50元包240小时，且其中每月收取费用y（元）与上网时间x（小时）的函数关系如图所示，小刚和小明家正好选择了这项上网业务．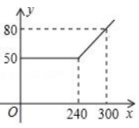

(1)、当 $x \geq 240$ 时，求y与x之间的函数关系式；

(2)、若小刚家10月份上网200小时，则他家应付多少元上网费？

(3)、若小明家10月份上网费用为62元，则他家该月的上网时间是多少小时？

查看试题解析

五、解答题（本大题共2小题，每小题9分，共18分）

21. 如图，Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，A＝10，BD平分∠ABC，如果点M，N分别为BD，BC．上的动点，
求：

(1)、画出点N关于BD的对称点 $N'$ ；

(2)、当 $N'$ 点（随点M和N的运动）运动到何处时， $C M + M N$ 取得最小值？并求出最小值．

查看试题解析
22. 先阅读下列一段文字，再回答问题．
已知平面内两点 $P_{1} (x_{1} ， y_{1}) ， P_{2} (x_{2} ， y_{2})$ ，这两点间的距离 $P_{1} P_{2} = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ ．同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间的距离公式可简化为 $| x_{2} - x_{1} |$ 或 $| y_{2} - y_{1} |$ ．

(1)、已知点 $A (2 ， 4)$ ， $B (- 3 ， - 8)$ ，试求A，B两点间的距离；

(2)、已知点A，B所在的直线平行于y轴，点B的纵坐标为2，A，B两点间的距离为4，求点A的纵坐标；

(3)、已知△ABC各顶点的坐标分别为 $A (- 2 ， 1)$ ， $B (1 ， - 1)$ ， $C (3 ， 2)$ ，你能判断△ABC的形状吗？说明理由．

查看试题解析

六、解答题（本大题共1小题，共12分）

23. 通过对下面数学模型的研究学习，解决下列问题：．

(1)、【模型呈现】某兴趣小组在从汉代数学家赵爽的弦图（如图1，由外到内含三个正方形）中提炼出两个三角形全等模型图（如图2），即“一线三等角”模型和“K字”模型．
请在上图2中选择其中一个模型进行证明 $△ A B C ≌ △ C D E$ ．

(2)、【模型应用】如图3，正方形ABCD中，AE⊥DE，DE-4，求△CDE的面积．

(3)、如图4，四边形ABCD中， $A D ∥ B C$ ， AB⊥BC，AD＝2，BC＝3， $D E ⊥ D C$ ， DE＝DC，求△ADE的面积．

查看试题解析

成绩/分	94	95	96	97	98	99
评委人数	2	1	3	1	2	1