江西省赣州市信丰县2023-2024学年九年级上学期期末数学试卷

试卷更新日期：2024-03-26 类型：期末考试

进入出卷网下载

一、选择题（本大题共6小题，每题3分，共18分）

1. 若 $\sqrt{a - 4}$ 有意义，则a的值可以是（）

A、﹣1 B、0 C、2 D、6

查看试题解析
2. 古典园林中的花窗通常利用对称构图，体现对称美．下面四个花窗图案，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，△ABC内接于⊙O，∠A＝30°，则∠BOC的度数为（）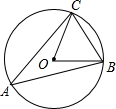

A、30° B、60° C、75° D、120°

查看试题解析
4. 把抛物线y=﹣2x²先向右平移1个单位长度，再向上平移2个单位长度后，所得函数的表达式为（　　）

A、y=﹣2（x+1）²+2 B、y=﹣2（x+1）²﹣2 C、y=﹣2（x﹣1）²+2 D、y=﹣2（x﹣1）²﹣2

查看试题解析
5. “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）．小亮随机地向大正方形内部区域投飞镖．若直角三角形两条直角边的长分别是2和1，则飞镖投到小正方形（阴影）区域的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 如图，点 $A$ ， $B$ ， $C$ ， $D$ 均在直线 $l$ 上，点 $P$ 在直线 $l$ 外，则经过其中任意三个点，最多可画出圆的个数为（）

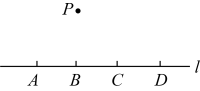A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题（本大题共6小题，每题3分，共18分）

7. 因式分解：x²﹣4y²＝.

查看试题解析
8. 若a、b是一元二次方程x²﹣3x+1＝0的两个实数根，则代数式a+b﹣ab的值为．

查看试题解析
9. 已知点P（2，﹣3）关于原点对称的点的坐标是．

查看试题解析
10. 不透明袋中有红、白两种颜色的小球，这些球除颜色外无其他差别．从袋中随机取出一个球是红球的概率为 $0.6$ ，若袋中有4个白球，则袋中红球有个．

查看试题解析
11. 已知点A（x₁ ， y₁），B（x₂ ， y₂）在抛物线y＝x²﹣3上，且0＜x₁＜x₂ ，则y₁y₂.（填“＜”或“＞”或“＝”）

查看试题解析
12. 如图，一副三角板的三个内角分别是90°，45°，45°和90°，60°，30°，按如图所示叠放在一起（点A，D，B在同一直线上），若固定△ABC，将△BDE绕着公共顶点B顺时针旋转α度（0＜α＜180），当边DE与△ABC的某一边平行时，相应的旋转角α的值为．

查看试题解析

三、（本大题5小题，每题6分，共30分）

13. 解方程x²﹣9＝0．

查看试题解析
14. 如果一个扇形的半径是6，圆心角的度数为60°，求扇形的面积．

查看试题解析
15. 用配方法解方程x²﹣4x﹣5＝0．

查看试题解析
16. 如图，将Rt△ABC绕点A按顺时针旋转一角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AC $= \sqrt{3}$ ， ∠B＝60°，求CD的长．

查看试题解析
17. 按要求画图：①仅用无刻度的直尺；②保留必要的画图痕迹．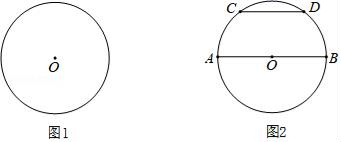

(1)、如图1，画出⊙O的一个内接矩形；

(2)、如图2，AB是⊙O的直径，CD是⊙O的弦，且CD∥AB，画出⊙O的一个内接正方形．

查看试题解析
18. 已知关于x的一元二次方程x²﹣2x﹣3m²＝0．

(1)、求证：方程总有两个不相等的实数根；

(2)、若方程的两个实数根分别为α，β，且α+2β＝5，求m的值．

查看试题解析

四、（本大题3小题，每题8分，共24分）

19. 如图，△ADE由△ABC绕点A按逆时针方向旋转90°得到，且点B的对应点D恰好落在BC的延长线上，AD，EC相交于点P.

(1)、求∠BDE的度数；

(2)、F是EC延长线上的点，且∠CDF＝∠DAC.判断DF和PF的数量关系，并证明.

查看试题解析
20. 4张相同的卡片上分别写有数字0、1、﹣2、3，将卡片的背面朝上，洗匀后从中任意抽取1张，将卡片上的数字记录下来；再从余下的3张卡片中任意抽取1张，同样将卡片上的数字记录下来．

(1)、第一次抽取的卡片上数字是负数的概率为；

(2)、小敏设计了如下游戏规则：当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时，甲获胜；否则，乙获胜．小敏设计的游戏规则公平吗？为什么？（请用树状图或列表等方法说明理由）

查看试题解析
21. 2023年亚运会在杭州顺利举行，亚运会吉祥物“江南忆”公仔爆红．据统计“江南忆”公仔在某电商平台8月份的销售量是5万件，10月份的销售量是7.2万件．

(1)、若该平台8月份到10月份的月平均增长率都相同，求月平均增长率是多少？

(2)、市场调查发现，某一间店铺“江南忆”公仔的进价为每件40元，若售价为每件80元，每天能销售20件，售价每降价0.5元，每天可多售出2件，为了推广宣传，商家决定降价促销，同时尽量减少库存，若使销售该公仔每天获利1400元，则售价应降低多少元？

查看试题解析

五、（本大题2小题，每题9分，共18分）

22. 如图，在△ABC中，AB＝4，∠C＝64°，以AB为直径的⊙O与AC相交于点D ， E为 $\hat{A B D}$ 上一点，且∠ADE＝40°．

(1)、求 $\hat{B E}$ 的长；

(2)、若∠EAD＝76°，求证：CB为⊙O的切线．

查看试题解析
23. 在一条笔直的滑道上有黑、白两个小球同向运动，黑球在 $A$ 处开始减速，此时白球在黑球前面 $70 c m$ 处．
小聪测量黑球减速后的运动速度 $v$ （单位： $c m / s$ ）、运动距离 $y$ （单位： $c m$ ）随运动时间 $t$ （单位： $s$ ）变化的数据，整理得下表．
运动时间 $t / s$
0
1
2
3
4
运动速度 $v / c m / s$
10
9.5
9
8.5
8
运动距离 $y / c m$
0
9.75
19
27.75
36
小聪探究发现，黑球的运动速度 $v$ 与运动时间 $t$ 之间成一次函数关系，运动距离 $y$ 与运动时间 $t$ 之间成二次函数关系．

(1)、直接写出 $v$ 关于 $t$ 的函数解析式和 $y$ 关于 $t$ 的函数解析式（不要求写出自变量的取值范围）

(2)、当黑球减速后运动距离为 $64 c m$ 时，求它此时的运动速度；

(3)、若白球一直以 $2 c m / s$ 的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由．

查看试题解析

六、（本大题共12分）

24. 直线y $= - \frac{2}{3}$ x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y $= - \frac{4}{3}$ x²+bx+c经过点A，B．M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．

(1)、求点B的坐标；

(2)、求抛物线的解析式；

(3)、点M在线段OA上运动，
①求线段PN的最大长度．
②连接AN，求△ABN面积的最大值．

查看试题解析

运动时间 $t / s$	0	1	2	3	4
运动速度 $v / c m / s$	10	9.5	9	8.5	8
运动距离 $y / c m$	0	9.75	19	27.75	36