江西省赣州市于都县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-26 类型:期末考试
一、选择题
-
1. 下列各曲线是根据不同的函数绘制而成的,其中是中心对称图形的是( )A、
 B、
B、 C、
C、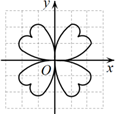 D、
D、 2. 将一元二次方程通过配方转化为的形式,下列结果中正确的是( )A、 B、 C、 D、3. 下列说法中,正确的是( )A、通过少量重复试验,可以用频率估计概率 B、事件发生的可能性越大,它的概率越接近1 C、某种彩票中奖的概率是 , 因此买100张该种彩票就一定会中奖 D、概率很小的事件不可能发生4. 如图,A,B,C是正方形网格中的三个格点,则是( )
2. 将一元二次方程通过配方转化为的形式,下列结果中正确的是( )A、 B、 C、 D、3. 下列说法中,正确的是( )A、通过少量重复试验,可以用频率估计概率 B、事件发生的可能性越大,它的概率越接近1 C、某种彩票中奖的概率是 , 因此买100张该种彩票就一定会中奖 D、概率很小的事件不可能发生4. 如图,A,B,C是正方形网格中的三个格点,则是( )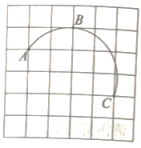 A、优弧 B、劣弧 C、半圆 D、无法判断5. 对于二次函数的图象的特征,下列描述正确的是( )A、开口向上 B、经过原点 C、对称轴是y轴 D、顶点在x轴上6. 近年来我国无人机产业迅猛发展,无人机驾驶员已正式成为国家认可的新职业.中国民用航空局的现有统计数据显示,从2017年底至2019年底,全国拥有民航局颁发的民用无人机驾驶执照的人数已由约2.44万人增加到约6.72万人.若设2017年底至2019年底,全国拥有民用无人机驾驶执照人数的年平均增长率为 ,则可列出关于 的方程为( ).A、 B、 C、 D、
A、优弧 B、劣弧 C、半圆 D、无法判断5. 对于二次函数的图象的特征,下列描述正确的是( )A、开口向上 B、经过原点 C、对称轴是y轴 D、顶点在x轴上6. 近年来我国无人机产业迅猛发展,无人机驾驶员已正式成为国家认可的新职业.中国民用航空局的现有统计数据显示,从2017年底至2019年底,全国拥有民航局颁发的民用无人机驾驶执照的人数已由约2.44万人增加到约6.72万人.若设2017年底至2019年底,全国拥有民用无人机驾驶执照人数的年平均增长率为 ,则可列出关于 的方程为( ).A、 B、 C、 D、二、填空题
-
7. 在平面直角坐标系中,点关于原点对称的点的坐标是.8. 若抛物线 ( )经过 ,则该抛物线的解析式为 .9. 如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形.若制作一个圆心角为160°的圆弧形窗帘轨道(如图2)需用此材料mm,则此圆弧所在圆的半径为mm.
 10. 下面是用配方法解关于x的一元二次方程的具体过程,
10. 下面是用配方法解关于x的一元二次方程的具体过程,解:第一步:
第二步:
第三步:
第四步: ,
以下四条语句与上面四步对应:“①移项:方程左边为二次项和一次项,右边为常数项;②求解:用直接开方法解一元二次方程;③配方:根据完全平方公式,在方程的两边各加上一次项系数一半的平方;④二次项系数化1,方程两边都除以二次项系数”,则第一步,第二步,第三步,第四步应对应的语句分别是 .
11. 如图,已知的两弦相交于E , 且点A为的中点,若 , 则的度数为 . 12. 如图,已知 , , , 将绕点A逆时针旋转,旋转角为(),当点D恰好落在的边上时,的长为 .
12. 如图,已知 , , , 将绕点A逆时针旋转,旋转角为(),当点D恰好落在的边上时,的长为 .
三、解答题
-
13. 计算:(1)、解方程:;(2)、如图,已知 , 把绕着点A顺时针旋转,使得点B与的延长线上的点D重合.求的度数.
 14. 如图,在⊙O中,= , ∠BOC=120°.求证:△ABC是等边三角形.
14. 如图,在⊙O中,= , ∠BOC=120°.求证:△ABC是等边三角形. 15. 数字“122”是中国道路交通事故报警电话,为推进“文明交通行动计划”,公安部将每年的12月2日定为“交通安全日”.数学社团决定从4名同学(小明,小红,小强,小芳)中通过抽签的方式确定2名同学去参加学校组织的“文明交通行动计划”宣传活动.抽签规则:将4名同学的姓名分别写在4张完全相同的卡片正面,把4张卡片的背面朝上,洗匀后放在桌子上,先从中随机抽取一张卡片,记下名字,再从剩余的3张卡片中随机抽取一张,记下名字,被抽到的同学去参加宣传活动.(1)、“小强被抽中”是事件(填“不可能”、“必然”、“随机”),第一次抽取卡片抽中小强的概率是;(2)、试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出小强被抽中的概率.16. 抛物线y=2x2平移后经过点A(0,3),B(2,3),求平移后的抛物线的表达式.17. 如图是的正方形网格纸.请仅用无刻度直尺作图,保留作图痕迹,不写作法.
15. 数字“122”是中国道路交通事故报警电话,为推进“文明交通行动计划”,公安部将每年的12月2日定为“交通安全日”.数学社团决定从4名同学(小明,小红,小强,小芳)中通过抽签的方式确定2名同学去参加学校组织的“文明交通行动计划”宣传活动.抽签规则:将4名同学的姓名分别写在4张完全相同的卡片正面,把4张卡片的背面朝上,洗匀后放在桌子上,先从中随机抽取一张卡片,记下名字,再从剩余的3张卡片中随机抽取一张,记下名字,被抽到的同学去参加宣传活动.(1)、“小强被抽中”是事件(填“不可能”、“必然”、“随机”),第一次抽取卡片抽中小强的概率是;(2)、试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出小强被抽中的概率.16. 抛物线y=2x2平移后经过点A(0,3),B(2,3),求平移后的抛物线的表达式.17. 如图是的正方形网格纸.请仅用无刻度直尺作图,保留作图痕迹,不写作法.图1
 图2
图2 (1)、如图1,线段的顶点在格点上,请在图中作以点A , B为顶点的四边形,使得该四边形是中心对称图形,且其顶点均在格点上(画出一个即可);(2)、如图2,矩形的顶点都在格点上,点M是边上任意一点,请在图中画出直线 , 使得直线平分矩形的面积.
(1)、如图1,线段的顶点在格点上,请在图中作以点A , B为顶点的四边形,使得该四边形是中心对称图形,且其顶点均在格点上(画出一个即可);(2)、如图2,矩形的顶点都在格点上,点M是边上任意一点,请在图中画出直线 , 使得直线平分矩形的面积.四、解答题
-
18. 如图,已知四边形是正方形,点E在上,将经顺时针旋转后与重合,再将向右平移后与重合.
 (1)、旋转的中心为点 , 旋转角的度数;(2)、如果连接 , 那是三角形;(3)、试猜想线段和的数量关系和位置关系,并说明理由.19. 如图,在直角坐标系内,已知点 .
(1)、旋转的中心为点 , 旋转角的度数;(2)、如果连接 , 那是三角形;(3)、试猜想线段和的数量关系和位置关系,并说明理由.19. 如图,在直角坐标系内,已知点 . (1)、图中点B的坐标是 ;(2)、点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;(3)、四边形ABCD的面积是 ;(4)、在y轴上找一点F,使 , 那么点F的坐标为 .20. 已知关于 的方程 .(1)、如果方程有两个不相等的实数根,求 的取值范围;(2)、若 ,求该方程的根.
(1)、图中点B的坐标是 ;(2)、点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;(3)、四边形ABCD的面积是 ;(4)、在y轴上找一点F,使 , 那么点F的坐标为 .20. 已知关于 的方程 .(1)、如果方程有两个不相等的实数根,求 的取值范围;(2)、若 ,求该方程的根.五、解答题
-
21. 如图,AC是⊙O的弦,过点O作OP⊥OC交AC于点P,在OP的延长线上取点B,使得BA=BP.
 (1)、求证:AB是⊙O的切线;(2)、若⊙O的半径为4,PC= , 求线段AB的长.22. 某商品成本价为16元/瓶,当定价为20元/瓶时,每天可售出60瓶.市场调查反映:销售单价每上涨1元,则每天少售出5瓶.设销售单价上涨x元,每天的利润为y元.(1)、每天的销售量为瓶,每瓶的利润为元(用含x的代数式表示).(2)、若日销售利润达到300元,求x的值.(3)、每天的销售利润能否达到400元?若能,求出x的值;若不能,说明理由.
(1)、求证:AB是⊙O的切线;(2)、若⊙O的半径为4,PC= , 求线段AB的长.22. 某商品成本价为16元/瓶,当定价为20元/瓶时,每天可售出60瓶.市场调查反映:销售单价每上涨1元,则每天少售出5瓶.设销售单价上涨x元,每天的利润为y元.(1)、每天的销售量为瓶,每瓶的利润为元(用含x的代数式表示).(2)、若日销售利润达到300元,求x的值.(3)、每天的销售利润能否达到400元?若能,求出x的值;若不能,说明理由.六、解答题
-
23. 综合与实践
问题提出:某兴趣小组开展综合实践活动:在中, , D为上一点, , 动点P以每秒1个单位的速度从C点出发,在三角形边上沿匀速运动,到达点A时停止,以为边作正方形设点P的运动时间为 , 正方形的面积为S , 探究S与t的关系
 (1)、初步感知:如图1,当点P由点C运动到点B时,
(1)、初步感知:如图1,当点P由点C运动到点B时,①当时, .
②S关于t的函数解析式为 .
(2)、当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象请根据图象信息,求S关于t的函数解析式及线段的长.(3)、延伸探究:若存在3个时刻()对应的正方形的面积均相等.① ▲ ;
②当时,求正方形的面积.