江西省南昌市青山湖区2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-26 类型：期末考试

进入出卷网下载

一、选择题（本大题共6个小题，每小题3分，共18分，每小题只有一个正确选项）

1. 下列方程中，是一元二次方程的是（）

A、 $x^{3} + 2 x = 0$ B、 $x (x - 3) = 0$ C、 $\frac{1}{x} - x^{2} = 1$ D、 $y - x^{2} = 4$

查看试题解析
2. 抛物线 $y = {(x - 1)}^{2} + 3$ 的顶点坐标是（）

A、 $(1 ， - 3)$ B、 $(- 1 ， 3)$ C、 $(- 1 ， - 3)$ D、 $(1 ， 3)$

查看试题解析
3. 下列事件中，是随机事件的是（）

A、投一次骰子，朝上面的点数是 $7$ B、任意画一个三角形，其内角和是 $180 °$ C、从一个只装有白球与黑球的袋中摸球，摸出红球 D、随意翻到一本书的某页，这页的页码是偶数

查看试题解析
4. 数学家是对世界数学的发展作出创造性工作的人士，他们运用他们的特殊知识与专业方法解决许多在科学领域的显著问题．下面的图形是用数学家名字命名的，其中是中心对称形的是（）

A、斐波那契螺旋线 B、阿基米德三角形 C、赵爽弦图 D、笛卡尔心形线

查看试题解析
5. 已知正比例函数 $y = m x (m \neq 0)$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象的一个交点坐标为 $(2 ， 4)$ ，则它们的另一个交点坐标是（）

A、 $(- 2 ， 4)$ B、 $(4 ， 2)$ C、 $(2 ， - 4)$ D、 $(- 2 ， - 4)$

查看试题解析
6. 如图， $A B$ 是 $⊙ O$ 的直径， $O D$ 垂直弦 $A C$ 于点 $D$ ， $D O$ 的延长线交 $⊙ O$ 于点 $E .$ 若 $A C = 4 \sqrt{2}$ ， $D E = 4$ ，则 $B C$ 的长是（）

A、 $1$
B、 $\sqrt{2}$
C、 $2$
D、 $4$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

7. 一元二次方程 $5 x^{2} + x - 3 = 0$ 的常数项是．

查看试题解析
8. 圆周率 $π$ 是无限不循环小数．历史上，祖冲之、刘徽、韦达、欧拉等数学家都对 $π$ 有过深入的研究．目前，超级计算机已计算出 $π$ 的小数部分超过 $31.4$ 万亿位．有学者发现，随着 $π$ 小数部分位数的增加，0－9这10个数字出现的频率趋于稳定接近相同，从 $π$ 的小数部分随机取出一个数字，估计数字是3的概率为．

查看试题解析
9. 若一元二次方程 $x^{2} - 3 x - 1 = 0$ 的两个根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2}$ 的值为．

查看试题解析
10. 如图， $⊙ O$ 的半径为3，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，则正六边形的面积为．

查看试题解析
11. 如图，为一幅三角板的两块，在 $△ B A D$ 中， $∠ B A D = 90 °$ ， $∠ A B D = 30 °$ ，在 $△ A B C$ 中， $∠ B C A = 45 °$ ，将 $△ B A D$ 绕点A逆时针旋转 $90 °$ 得到 $△ C A E$ ，连接 $C E$ ，则 $∠ B C E$ 的大小为．

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A B = 10 ， A D = 6$ ，以 $A B$ 为直径在矩形内作半圆，点P为半圆上的一动点（不与A，D重合），连接 $A P 、 D P$ ，当 $△ A D P$ 为锐角等腰三角形时， $A P$ 的长为．

查看试题解析

三、（本大题共5小题，每小题6分，共30分）

13. 用适当方法解下列方程：

(1)、 $x (x - 4) = 0$ ；

(2)、 $x^{2} - 2 x - 3 = 0$ ．

查看试题解析
14. 临近毕业，甲、乙、丙三人相约去餐馆聚餐，丙先到达餐馆，选了一张方桌坐在如图所示的座位上，甲到达餐馆后，从座位①、②、③中随机选择一个坐下，乙到达餐馆后，从剩下的座位中再随机选择一个坐下．

(1)、甲坐在①号座位上的概率是；

(2)、用列表法或画树状图的方法，求甲、乙两人恰好相邻而坐的概率．

查看试题解析
15. 如图，在方格网中已知格点 $△ A B C$ 和点 $P$ ，请仅用无刻度直尺完成以下作图．

(1)、画出 $△ A^{'} B^{'} C^{'}$ ，使得 $△ A^{'} B^{'} C^{'}$ 和 $△ A B C$ 关于点 $P$ 成中心对称；

(2)、请在方格网中标出所有使以点 $A$ ， $B$ ， $P$ ， $D$ 为顶点的四边形是平行四边形的 $D$ 点．

查看试题解析
16. 如图，线段 $A C$ 过圆心O，交 $⊙ O$ 于B，C两点，线段 $A E$ 交 $⊙ O$ 于D，E两点，且 $A D = O B$ ， $∠ A = 30 °$ ，求 $∠ E O C$ 的度数．

查看试题解析
17. 南昌市秋水广场喷水池中心O有一雕塑 $O A$ ，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立直角坐标系，点 $A (0 ， 4)$ 在y轴上，x轴上的点 $C (－ 4 ， 0)$ 和点D为水柱的落水点，水柱所在抛物线第一象限部分的函数解析式为 $y = - x^{2} + b x + c$ ．

(1)、求水柱所在抛物线第一象限部分的函数解析式；

(2)、求两个水柱的最高点M，N之间的距离．

查看试题解析

四、（本大题共3小题，每小题8分，共24分）

18. 近年来，诈骗分子较为猖狂，诈骗手段不断更新，据有关部门统计，2022年全年全国电信诈骗共计达到 $2$ 万亿元．为有效提高学生防诈反诈能力，学校开展了“防诈反诈”讲座后进行了“防诈反诈”知识竞赛，并从七、八年级各随机选取了 $20$ 名同学的竞赛成绩进行了整理、描述和分析（成绩得分用 $x$ 表示，其中 $A$ ： $0 \leq x < 85$ ， $B$ ： $85 \leq x < 90$ ， $C$ ： $90 \leq x < 95$ ， $D$ ： $95 \leq x \leq 100$ ，得分在 $90$ 分及以上为优秀）．下面给出了部分信息：
七年级 $C$ 组同学的分数分别为： $94$ ， $92$ ， $93$ ， $91$ ；
八年级C组同学的分数分别为： $91$ ， $92$ ， $93$ ， $93$ ， $94$ ， $94$ ， $94$ ， $94$ ， $94$ ．
七、八年级选取的学生竞赛成绩统计表
年级
平均数
中位数
众数
优秀率
七
$91$
$a$
$95$
$m$
八
$91$
$93$
$b$
$65 %$

(1)、填空： $a =$ ， $b =$ ， $m =$ ；

(2)、根据以上数据，你认为该校七、八年级学生在“防诈反诈”知识竞赛中，哪个年级学生对“防诈反诈”的了解情况更好？请说明理由；（写出一条理由即可）

(3)、该校现有学生七年级 $780$ 名，八年级 $800$ 名，请估计这两个年级竞赛成绩为优秀的学生总人数．

查看试题解析
19. 如图， $B D$ 是 $⊙ O$ 的直径，A是 $B D$ 延长线上的一点，点E在 $⊙ O$ 上， $B C ⊥ A E$ ，交 $A E$ 的延长线于点C， $B C$ 交 $⊙ O$ 于点F，且点E是 $\overset{⌢}{D F}$ 的中点．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、若 $A D = 3 ， A E = 3 \sqrt{2}$ ，求 $⊙ O$ 的半径．

查看试题解析
20. 如图，一次函数 $y = x + 3$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于点 $A (1 ， m)$ ，与 $x$ 轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ，

(1)、求反比例函数的表达式；

(2)、已知点 $P$ 为反比例函数 $y = \frac{k}{x}$ 图象上一点， $S_{△ O B P} = 2 S_{△ O A C}$ ，求点 $P$ 的坐标.

查看试题解析

五、（本大题共2小题，每小题9分，共18分）

21. 已知关于 $x$ 的方程 $k^{2} x^{2} - 2 (k - 1) x + 1 = 0$ 有两个实数根 $x_{1}$ 、 $x_{2}$ .

(1)、求 $k$ 的取值范围.

(2)、若 $x_{1}$ 、 $x_{2}$ 满足等式 $| x_{1} + x_{2} | = 5 x_{1} x_{2} - 1$ ，求 $k$ 的值.

查看试题解析
22. 如图，在正方形 $A B C D$ 中，点 $E$ 是对角线 $A C$ 上一动点，连接 $D E$ ，作 $E F ⊥ D E$ 交 $B C$ 于点 $F$ ，以 $E D$ 和 $E F$ 为邻边作矩形 $E F G D$ ．

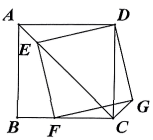(1)、猜想： $A E$ ， $C G$ 的位置关系是；

(2)、求证： $△ D A E ≌ △ D C G$ ．

查看试题解析

六、（本大题1小题，12分）

23. 如图，已知抛物线C： $y = a x^{2} + b x + c$ 的对称轴为直线 $x = - 1$ ，且抛物线经过M $(1 ， 0) ， C (0 ， 3)$ 两点，与x轴交于点N．

(1)、点N（，）；

(2)、若抛物线 $C_{1}$ 与抛物线C关于y轴对称，求抛物线 $C_{1}$ 的解析式；

(3)、若抛物线 $C_{n}$ 的解析式为 $y = - (x + 1) (x - 2 - n) (n = 1 ， 2 ， 3 ， ⋯)$ ，抛物线 $C_{n}$ 的顶点坐标为 $P_{n}$ ，与x轴的交点坐标为A， $B_{n}$ （点A在点 $B_{n}$ 的左边）
①求： $A B_{1} + A B_{2} + A B_{3} + ⋯ A B_{100}$ 的值；
②判断抛物线的顶点 $P_{1} ， P_{2} ， P_{3}$ ， …， $P_{n}$ 是否在一条直线上，若在，请直接写出直线解析式；不在，请说明理由．

查看试题解析

年级	平均数	中位数	众数	优秀率
七	$91$	$a$	$95$	$m$
八	$91$	$93$	$b$	$65 %$