江西省赣州市赣县2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-26 类型:期末考试
一、选择题(本大题共6小题.)
-
1. 下列长度的三条线段能组成三角形的是( )A、1cm 2cm 3cm B、6cm 2cm 3cm C、4cm 6cm 8cm D、5cm 12cm 6cm2. 如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为( )
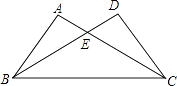 A、2 B、3 C、4 D、53. 甲骨文是我国目前发现最早的文字,其图画性强的特点非常明显,下列甲骨文图画是轴对称的是( )A、
A、2 B、3 C、4 D、53. 甲骨文是我国目前发现最早的文字,其图画性强的特点非常明显,下列甲骨文图画是轴对称的是( )A、 B、
B、 C、
C、 D、
D、 4. 点关于x轴的对称点的坐标为( )A、 B、 C、 D、5. 下列运算不正确的是( )A、 B、 C、 D、6. 解方程去分母,两边同乘后的式子为( )A、 B、 C、 D、
4. 点关于x轴的对称点的坐标为( )A、 B、 C、 D、5. 下列运算不正确的是( )A、 B、 C、 D、6. 解方程去分母,两边同乘后的式子为( )A、 B、 C、 D、二、填空题(本大题共6小题)
-
7. 因式分解: .8. 如图,若 , , 则的度数为 .
 9. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接并延长到D,使;连接并延长到E,使 , 由和全等得到 . 那么判定其全等的依据是(用三个字母表示).
9. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接并延长到D,使;连接并延长到E,使 , 由和全等得到 . 那么判定其全等的依据是(用三个字母表示). 10. 计算: = .11. 如图,在中, , 平分 , 则的面积是 .
10. 计算: = .11. 如图,在中, , 平分 , 则的面积是 . 12. 如图,B是射线上动点, , 若为等腰三角形,则的度数可能是 .
12. 如图,B是射线上动点, , 若为等腰三角形,则的度数可能是 .
三、(本大题共5小题)
-
13.(1)、化简:;(2)、如图, , , . 求证: .
 14. 如图,在中,是边上的高,是的平分线,求的度数.
14. 如图,在中,是边上的高,是的平分线,求的度数. 15. 先化简,再求值: , 其中 .16. 在的方格纸中,的三个顶点都在格点上,请用无刻度的直尺在图1、图2中画出与成轴对称的格点三角形(不重复画).
15. 先化简,再求值: , 其中 .16. 在的方格纸中,的三个顶点都在格点上,请用无刻度的直尺在图1、图2中画出与成轴对称的格点三角形(不重复画).
 17. 斑马线前“车让人”,不仅体现着一座城市对生命的尊重,也直接反映了城市的文明程度.如图,某路口的斑马线路段横穿双向行驶车道,其中米,在绿灯亮时,小明共用12.5秒通过 , 其中通过的速度是通过的速度的1.5倍,求小明通过时的速度.
17. 斑马线前“车让人”,不仅体现着一座城市对生命的尊重,也直接反映了城市的文明程度.如图,某路口的斑马线路段横穿双向行驶车道,其中米,在绿灯亮时,小明共用12.5秒通过 , 其中通过的速度是通过的速度的1.5倍,求小明通过时的速度.
四、(本大题共3小题)
-
18. 王强同学用10块高度都是2的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( , ),点和分别与木墙的顶端重合.
 (1)、求证:;(2)、求两堵木墙之间的距离.19. 如图,的三个顶点的坐标分别为 , , .
(1)、求证:;(2)、求两堵木墙之间的距离.19. 如图,的三个顶点的坐标分别为 , , . (1)、若与关于y轴对称,则A,C的对称点 , 的坐标分别为 , .(2)、求的面积.(3)、在y轴上求作一点P,使的和最小.(保留作图痕迹)20. 如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)、若与关于y轴对称,则A,C的对称点 , 的坐标分别为 , .(2)、求的面积.(3)、在y轴上求作一点P,使的和最小.(保留作图痕迹)20. 如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.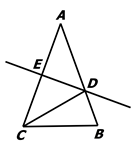 (1)、若∠A = 40°,求∠DCB的度数.(2)、若AE=4,△DCB的周长为14,求△ABC的周长.
(1)、若∠A = 40°,求∠DCB的度数.(2)、若AE=4,△DCB的周长为14,求△ABC的周长.五、(本大题共2小题)
-
21. 通过用两种不同的方法计算同一个图形的面积,可以得到一个代数恒等式.如图①是一个长为 , 宽为m的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图②的方式拼成一个大正方形.
 (1)、【知识生成】
(1)、【知识生成】请用两种不同的方法表示图②中阴影部分的面积(直接用含m,n的代数式表示):
方法一:;
方法二:;
(2)、【得出结论】根据(1)中的结论,请你写出代数式之间的等量关系为;
(3)、【知识迁移】根据(2)中的等量关系,解决如下问题:
已知实数a,b满足: , , 求的值.
22. 在中, , , 是边上的高,点E为直线上点,且 . (1)、如图1,当点E在边上时,求证:为等边三角形;(2)、如图2,当点E在的延长线上时,求证:为等腰三角形.
(1)、如图1,当点E在边上时,求证:为等边三角形;(2)、如图2,当点E在的延长线上时,求证:为等腰三角形.六、(本大题共1小题)
-
23. 【问题背景】
在四边形中, , , , E、F分别是、上的点,且 , 试探究图1中线段之间的数量关系.
 (1)、【初步探索】
(1)、【初步探索】小亮同学认为:延长到点G,使 , 连接 , 先证明 , 再证明 , 则可得到之间的数量关系是 .
(2)、【探索延伸】在四边形中如图2, , , E、F分别是上的点, , 上述结论是否仍然成立?说明理由.
(3)、【结论运用】如图3, , , , , , , , 直接写出的长度.