江西省2024年中考数学一模备考练习卷
试卷更新日期:2024-03-26 类型:中考模拟
一、 单项选择题(本大题共6小题,每小题3分,共18分)
-
1. 比大1的数是( )A、1 B、 C、 D、12. 故宫又称紫禁城,位于北京中轴线的中心,占地面积高达平方米,在世界宫殿建筑群中面最大.请将用科学记数法表示应为( )
 A、 B、 C、 D、3. 如图, , 点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( )
A、 B、 C、 D、3. 如图, , 点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( ) A、45° B、50° C、57.5° D、65°4. 某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( )
A、45° B、50° C、57.5° D、65°4. 某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( )
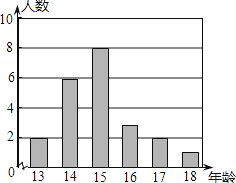 A、15.5,15.5 B、15.5,15 C、15,15.5 D、15,155. 已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )A、
A、15.5,15.5 B、15.5,15 C、15,15.5 D、15,155. 已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )A、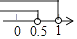 B、
B、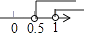 C、
C、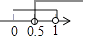 D、
D、 6. 二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象是( )
6. 二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象是( )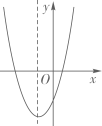 A、
A、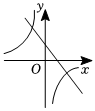 B、
B、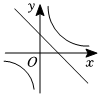 C、
C、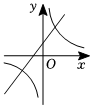 D、
D、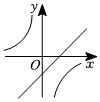
二、填空题(本大题共6小题,每小题3分,共18分)
-
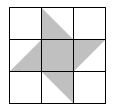
7. 如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,那么小球最终停留在黑色区域的概率是 .
 8. 若关于x的一元二次方程有两个不相等的实数根,则a的取值范围是.9. 如图,半径为3的经过原点O和点 , 点B是y轴左侧优弧上一点,则为 .
8. 若关于x的一元二次方程有两个不相等的实数根,则a的取值范围是.9. 如图,半径为3的经过原点O和点 , 点B是y轴左侧优弧上一点,则为 .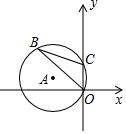 10. 使分式与的值相等的x的值为 .11. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中、分别表示去年、今年水费(元)与用水量()之间的关系.小雨家去年用水量为150 , 若今年用水量与去年相同,水费将比去年多元.
10. 使分式与的值相等的x的值为 .11. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中、分别表示去年、今年水费(元)与用水量()之间的关系.小雨家去年用水量为150 , 若今年用水量与去年相同,水费将比去年多元.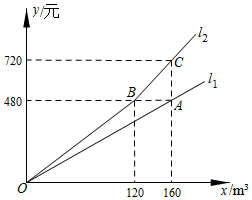 12. 数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点落在边的点处,其中 , 且 , 则矩形的面积为
12. 数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点落在边的点处,其中 , 且 , 则矩形的面积为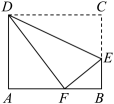
三、解答题(本大题共5小题,每小题6分,共30分)
-
13.(1)、计算: .(2)、如图,在平行四边形中,点 , 分别在边 , 上,且四边形为正方形求证: .
 14. 解分式方程: .15. 四张卡片上分别有2022年北京冬奥会会徽、志愿者标志、吉祥物冰墩墩、雪容融图案,它们形状、大小、背面完全一样,现把四张卡片背面朝上打乱放在桌面上.
14. 解分式方程: .15. 四张卡片上分别有2022年北京冬奥会会徽、志愿者标志、吉祥物冰墩墩、雪容融图案,它们形状、大小、背面完全一样,现把四张卡片背面朝上打乱放在桌面上. (1)、小志同学从中抽取一张是冬奥会会徽卡片是事件(填“随机”、“不可能”或“必然”);(2)、小志同学从中一次性抽取两张卡片,请你用列表法或画树状图法表示出这次抽取所有可能的结果,并求出正好是两张吉祥物图案的概率.16. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)、小志同学从中抽取一张是冬奥会会徽卡片是事件(填“随机”、“不可能”或“必然”);(2)、小志同学从中一次性抽取两张卡片,请你用列表法或画树状图法表示出这次抽取所有可能的结果,并求出正好是两张吉祥物图案的概率.16. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).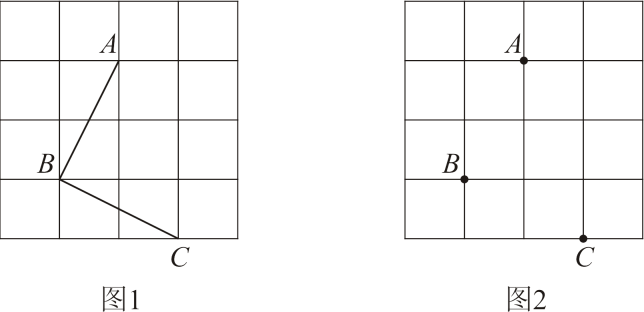 (1)、在图1中作的角平分线;(2)、在图2中过点C作一条直线l,使点A,B到直线l的距离相等.17. 如图,已知一次函数的图象与轴、轴分别交于、两点,与反比例函数的图象分别交于、两点,点 , 点是线段的中点.
(1)、在图1中作的角平分线;(2)、在图2中过点C作一条直线l,使点A,B到直线l的距离相等.17. 如图,已知一次函数的图象与轴、轴分别交于、两点,与反比例函数的图象分别交于、两点,点 , 点是线段的中点.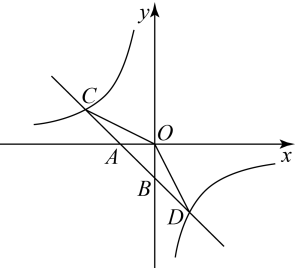 (1)、求一次函数与反比例函数的解析式;(2)、求的面积;(3)、直接写出时自变量的取值范围.
(1)、求一次函数与反比例函数的解析式;(2)、求的面积;(3)、直接写出时自变量的取值范围.四、解答题(本大题共3小题,每小题8分,共24分)
-
18. 根据市场需求,某书城准备购进甲、乙两种青少年喜欢的读本进行销售,它们的进价和售价如下表.
读本
进价(元/本)
售价(元/本)
甲
30
45
乙
20
30
现计划用不超过1850元购进这两种读本共80本,并将这80本读本全部售完,
设购进甲种读本x本,这两种读本的总利润为y元.
(1)、求y与x的函数关系式.(2)、该书城如何进货才能获得最大利润?最大利润是多少?19. 如图所示的是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平线AE垂直,AB=154cm,∠A=30°,另一根辅助支架DE=78cm,∠E=60°.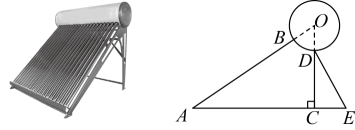 (1)、求CD的长度.(结果保留根号)(2)、求OD的长度.(结果保留一位小数.参考数据:≈1.414,≈1.732)20. 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且 = ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)、求CD的长度.(结果保留根号)(2)、求OD的长度.(结果保留一位小数.参考数据:≈1.414,≈1.732)20. 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且 = ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G. (1)、证明:GF是⊙O的切线;(2)、若AG=6,GE=6 ,求⊙O的半径.
(1)、证明:GF是⊙O的切线;(2)、若AG=6,GE=6 ,求⊙O的半径.五、解答题(本大题共2小题,每小题9分,共18分)
-
21. 目前人们的支付方式日益增多,主要有:

A.微信 B.支付宝 C.信用卡 D.现金
某超市对一天内消费者的支付方式进行了统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,回答下列问题:
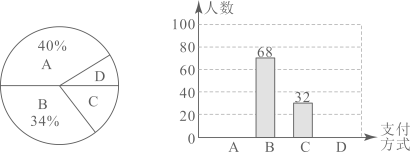 (1)、本次一共调查了名消费者;(2)、补全条形统计图,在扇形统计图中D种支付方式所对应的圆心角为 ▲ ;(3)、该超市本周内约有2000名消费者,估计使用A和B两种支付方式的消费者的人数的总和.22. 如图
(1)、本次一共调查了名消费者;(2)、补全条形统计图,在扇形统计图中D种支付方式所对应的圆心角为 ▲ ;(3)、该超市本周内约有2000名消费者,估计使用A和B两种支付方式的消费者的人数的总和.22. 如图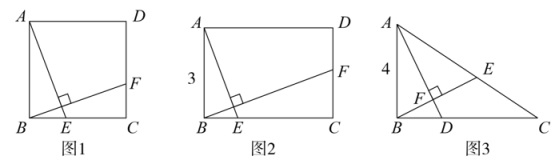 (1)、综合与探究,如图1,在正方形中,点E , F分别在边上,且 , 则线段与的之间的数量关系为;(2)、【类比探究】如图2,在矩形中, , , 点E , F分别在边上,且 , 请写出线段与的数量关系,并证明你的结论.(3)、【拓展延伸】如图3,在中, , , , D为上一点,且 , 连接 , 过点B作于点F , 交于点E , 求的长.
(1)、综合与探究,如图1,在正方形中,点E , F分别在边上,且 , 则线段与的之间的数量关系为;(2)、【类比探究】如图2,在矩形中, , , 点E , F分别在边上,且 , 请写出线段与的数量关系,并证明你的结论.(3)、【拓展延伸】如图3,在中, , , , D为上一点,且 , 连接 , 过点B作于点F , 交于点E , 求的长.六、解答题(本大题共12分)
-
23. 如图,抛物线与x轴交于A(2,0),B(-1,0)两点,与y轴交于点C,连接BC,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
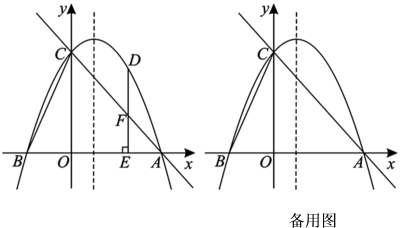 (1)、求抛物线的表达式;(2)、当线段DF的长度最大时,求D点的坐标;(3)、抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与△BOC相似?若存在,求出m的值;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、当线段DF的长度最大时,求D点的坐标;(3)、抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与△BOC相似?若存在,求出m的值;若不存在,请说明理由.