重庆市南岸区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-26 类型:期末考试
一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的.
-
1. 如图,在中, , , , 则的值为( )
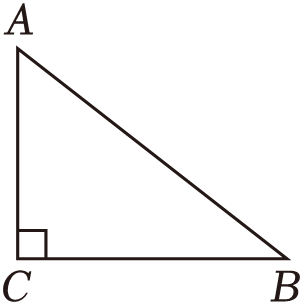 A、3 B、4 C、5 D、62. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、3. 若关于的一元二次方程有两个相等的实数根,则实数的值为( )A、 B、 C、 D、94. 如图,由相同大小的正方体积木堆叠而成的立体图形.如果拿走图中的甲、乙、丙、丁中的一个积木,此图形主视图的形状会改变,则拿走的积木是( )
A、3 B、4 C、5 D、62. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、3. 若关于的一元二次方程有两个相等的实数根,则实数的值为( )A、 B、 C、 D、94. 如图,由相同大小的正方体积木堆叠而成的立体图形.如果拿走图中的甲、乙、丙、丁中的一个积木,此图形主视图的形状会改变,则拿走的积木是( )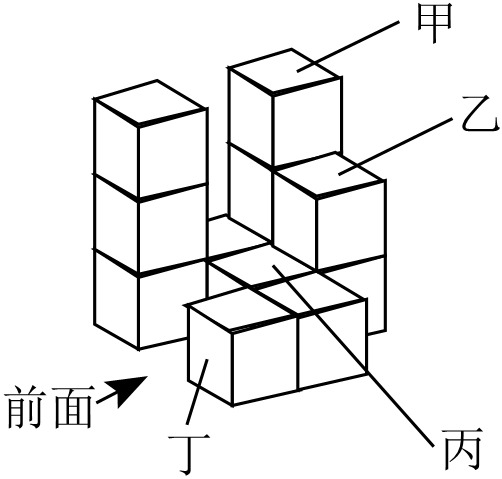 A、甲 B、乙 C、丙 D、丁5. 将抛物线向上平移2个单位长度,再向左平移3个单位长度,得到抛物线 , 则b , c的值为( )A、 , B、 , C、 , D、 ,6. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( )
A、甲 B、乙 C、丙 D、丁5. 将抛物线向上平移2个单位长度,再向左平移3个单位长度,得到抛物线 , 则b , c的值为( )A、 , B、 , C、 , D、 ,6. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( )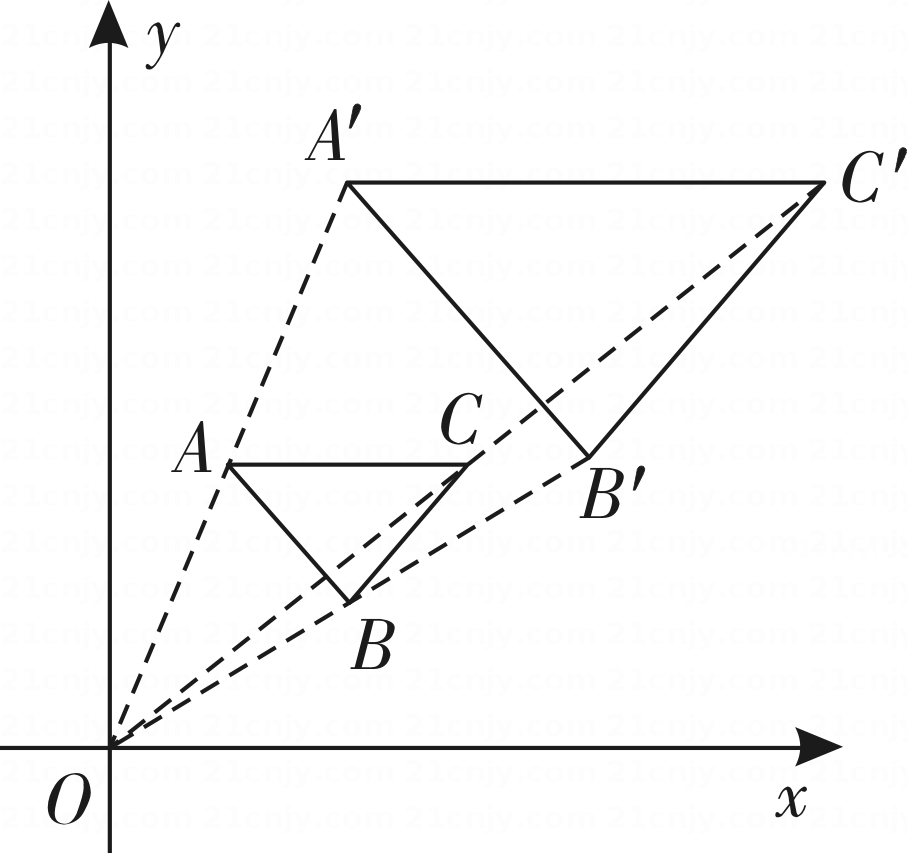 A、 B、 C、 D、7. 如图,在矩形中, , 分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线分别交于点E,F,则的长为( )
A、 B、 C、 D、7. 如图,在矩形中, , 分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线分别交于点E,F,则的长为( ) A、 B、 C、 D、8. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )
A、 B、 C、 D、8. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )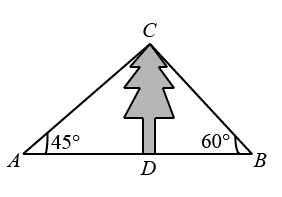 A、 B、 C、 D、9. 若数使关于的一元二次方程有两个不相等的实数解,且使关于的分式方程的解为非负整数,则满足条件的的值为( )A、1 B、3 C、5 D、710. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( )
A、 B、 C、 D、9. 若数使关于的一元二次方程有两个不相等的实数解,且使关于的分式方程的解为非负整数,则满足条件的的值为( )A、1 B、3 C、5 D、710. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( ) A、12 B、14 C、18 D、24
A、12 B、14 C、18 D、24二、填空题:(本大题8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上.
-
11. 一元二次方程的两根为 .12. 若 , 则 .13. 如图,菱形的对角线、相交于点O , E为的中点, . 则 .
 14. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点 , , 在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m.
14. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点 , , 在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m.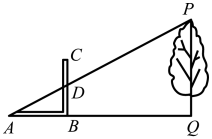 15. 如图为一个几何体的三视图,主视图和左视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为 .
15. 如图为一个几何体的三视图,主视图和左视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为 . 16. 已知二次函数 , 当自变量和时,函数值 , 则该抛物线的对称轴为 .17. 如图,在中, , D , E分别是的中点,把沿着翻折,点B恰好在边上的F处,若 , 则 . (用含k的代数式表示)
16. 已知二次函数 , 当自变量和时,函数值 , 则该抛物线的对称轴为 .17. 如图,在中, , D , E分别是的中点,把沿着翻折,点B恰好在边上的F处,若 , 则 . (用含k的代数式表示) 18. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b.CF与DE交于点H,延长AE,BF交于点G,AG长为c.
18. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b.CF与DE交于点H,延长AE,BF交于点G,AG长为c.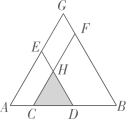 (1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .
(1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .三、解答题:(本大题8个小题,19题8分;20-26题每小题8分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡中对应的位置上.
-
19. 扬州是个好地方,有着丰富的旅游资源.某天甲、乙两人来扬州旅游,两人分别从 , , 三个景点中随机选择一个景点游览.(1)、甲选择景点的概率为;(2)、请用画树状图或列表的方法,求甲、乙两人中至少有一人选择景点的概率.20. 解方程:(1)、;(2)、 .21. 如图,在中,D是边上一点.
 (1)、请用尺规作图,在上找一点E , 作 , 保留作图痕迹.(2)、若 , 求与四边形的面积比.22. 如图,一次函数与反比例函数的图象交于 , 两点.
(1)、请用尺规作图,在上找一点E , 作 , 保留作图痕迹.(2)、若 , 求与四边形的面积比.22. 如图,一次函数与反比例函数的图象交于 , 两点. (1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时,x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M , 交反比例函数的图象于点Q , 若面积为3,求点P的坐标.23. 综合与实践活动中,要利用测角仪测量塔的高度,如图,塔前有一座高为的观景台,已知 , 的坡度为 , 点E , C , A在同一条水平直线上.某学习小组在观景台C处测得塔顶部B的仰角为 , 在观景台D处测得塔顶部B的仰角为 .
(1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时,x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M , 交反比例函数的图象于点Q , 若面积为3,求点P的坐标.23. 综合与实践活动中,要利用测角仪测量塔的高度,如图,塔前有一座高为的观景台,已知 , 的坡度为 , 点E , C , A在同一条水平直线上.某学习小组在观景台C处测得塔顶部B的仰角为 , 在观景台D处测得塔顶部B的仰角为 .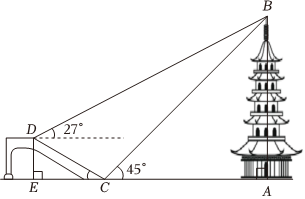 (1)、求的长;(2)、求塔的高度.(结果保留个位)
(1)、求的长;(2)、求塔的高度.(结果保留个位)(参考数据:tan27°≈0.5,≈1.7)
24. 为了加强中小学学生的劳动教育,2024年计划将该区的土地作为社会实践基地,该基地准备种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位:元)与其种植面积x(单位:)的函数关系 , 其中;乙种蔬菜的种植成本为50元 .(1)、设2024年甲乙两种蔬菜总种植成本为w元,如何分配两种蔬菜的种植面积,使w最小?(2)、学校计划今后每年在这土地上,均按(1)中方案种植蔬菜,因技术改进,预计种植成本逐年下降.若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2026年的总种植成本为28920元?25. 如图,已知抛物线与x轴交于和两点,与y轴交于点C . (1)、求抛物线的函数解析式;(2)、若直线与抛物线交于点D , 与直线交于点F , 交x轴交于点E . 当取得最大值时,求m的值和的最大值;(3)、若抛物线的顶点为P , Q是该抛物线对称轴上一点,在平面内确定一点R , 使得以点C , R , P , Q为顶点的四边形是菱形,求点R的坐标.26. 平行四边形中,点E在边上,对角线交于点F .
(1)、求抛物线的函数解析式;(2)、若直线与抛物线交于点D , 与直线交于点F , 交x轴交于点E . 当取得最大值时,求m的值和的最大值;(3)、若抛物线的顶点为P , Q是该抛物线对称轴上一点,在平面内确定一点R , 使得以点C , R , P , Q为顶点的四边形是菱形,求点R的坐标.26. 平行四边形中,点E在边上,对角线交于点F . (1)、如图1,在平行四边形中, , , 求证:;(2)、如图2,在平行四边形中, , , 那么与的长有什么关系?请证明你的结论;(3)、如图3,在平行四边形中, , , , , 求的长.
(1)、如图1,在平行四边形中, , , 求证:;(2)、如图2,在平行四边形中, , , 那么与的长有什么关系?请证明你的结论;(3)、如图3,在平行四边形中, , , , , 求的长.