重庆市江津区2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-26 类型：期末考试

进入出卷网下载

一、选择题：（本大题10个小题，每小题4分，共40分）

1. 习近平总书记指出：发展新能源汽车是我国从汽车大国走向汽车强国的必由之路．下列四款新能源汽车的标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中属于必然事件的是（）

A、直径是圆中最长的弦 B、打开手机就有未接电话 C、李明同学下次数学考试满分 D、某学生立定跳远的最好成绩是10米

查看试题解析
3. 如果方程 $(p - 2) x^{p^{2} - 2} - x + 3 = 0$ 是关于x的一元二次方程，则P的值是（）

A、2 B、 $- 2$ C、 $\pm 2$ D、3

查看试题解析
4. 点 $(- 1 ， y_{1})$ ， $(2 ， y_{2})$ 都在函数 $y = - {(x - 1)}^{2} + 2$ 的图象上，则 $y_{1} ， y_{2}$ 的大小关系为（）

A、 $y_{1} < y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} > y_{2}$ D、无法确定

查看试题解析
5. 如图，用若干根相同的小木棒拼成图形，拼第①个图形需要 $6$ 根小木棒，拼第②个图形需要 $11$ 根小木棒，拼第③个图形需要 $16$ 根小木棒……则按照这样的方法拼成的第⑥个图形需要（）根小木棒．

A、 $26$ B、 $30$ C、 $31$ D、 $36$

查看试题解析
6. 如图，将 $△ A B C$ 绕着点B逆时针旋转 $60 °$ 后得到 $△ A^{'} B C^{'}$ ，若 $B C = 3$ ，则 $\overset{⌢}{C C^{'}}$ 的长度为（）

A、3 B、 $π$ C、 $\frac{3}{2} π$ D、 $\frac{1}{2} π$

查看试题解析
7. 在“双减”政策的推动下，我区某中学学生每天书面作业时长明显减少，2022 年下学期平均每天书面作业时长为90分钟，经过2023年上学期和2023年下学期两次调整后，2023年下学期平均每天书面作业时长为70分钟，设该校这两学期平均每天书面作业时长每学期的下降率为x ，则可列方程为（）

A、 $70 (1 + x^{2}) = 90$ B、 $70 {(1 + x)}^{2} = 90$ C、 $90 (1 - x^{2}) = 70$ D、 $90 {(1 - x)}^{2} = 70$

查看试题解析
8. 如图所示一个圆柱体容器内装入一些水，截面AB在圆心 $O$ 下方，若 $⊙ O$ 的直径为 $26 c m$ ，水面宽 $A B = 24 c m$ ，则水的最大深度为（）

A、 $5 c m$ B、 $7 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
9. 如图，正方形 $A B C D$ 的边长为4， $∠ E A F = 45 °$ ，将 $△ A B E$ 绕点 $A$ 按顺时针方向旋转 $90 °$ 得到 $△ A D G$ ．若 $B E = 1$ ，则 $D F$ 的长为（）

A、3 B、 $\sqrt{7}$ C、 $\frac{12}{5}$ D、4

查看试题解析
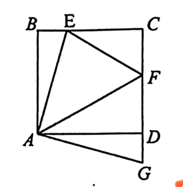10. 对于若干个单项式，我们先将任意两个单项式作差，再将这些差的绝对值进行求和并化简，这样的运算称为对这若干个单项式作“差绝对值运算”．例如：对 $2 ， 3 ， 4$ 作“差绝对值运算”，得到 $| 2 - 3 | + | 2 - 4 | + | 3 - 4 | = 4$ ，则
$①$ 对 $1 ， 3 ， 4 ， 7$ 作“差绝对值运算”的结果是 $19$ ； $②$ 对 $x^{2} ， x ， - 3 (x^{2} > x > - 3)$ 进行“差绝对值运算”的结果是 $38$ ，则 $x = \pm 4$ ； $③$ 对 $a ， b ， c$ （互不相等）进行“差绝对值运算”的结果一共有 $7$ 种．
以上说法中正确的个数为（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析

二、填空题：（本大题8个小题，每小题4分，共32分）

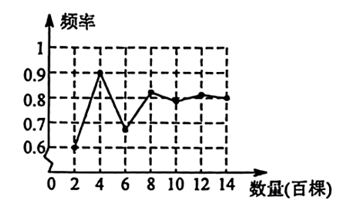
11. 点 $(5 ， 4)$ 关于原点对称的点的坐标是．

查看试题解析
12. 如果m是方程 $x^{2} - 2 x - 6 = 0$ 的一个根，那么代数式 $2 m^{2} - 4 m + 1$ 的值为．

查看试题解析
13. 某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图，由此可估计这种树苗移植成活的概率约为（精确到 $0.1$ ）

查看试题解析
14. 如图，抛物线y=ax²与直线y=bx+c的两个交点坐标分别为A（-2，4），B（1，1），则不等式ax²＞bx+c的解集是.

查看试题解析
15. 如图，点 $O$ 是以 $A B$ 为直径的半圆的圆心，以 $A$ 为圆心， $A O$ 为半径的弧交半圆于点 $C$ ，以 $B$ 为圆心， $B O$ 为半径的弧交半圆于点 $D$ ，点F是 $\overset{⌢}{C D}$ 上一点， $B F = 6$ ， $A F = 8$ ．则阴影部分的面积为（结果保留 $π$ ）

查看试题解析
16. 如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{9} (x - 9) (x + 2)$ $，$ 则铅球被推出的水平距离 $O A$ 为 m．

查看试题解析
17. 如果关于 $x$ 的一元二次方程 $x^{2} + 4 x + m + 2 = 0$ 有实数根，且关于 $y$ 的分式方程 $\frac{m y + 1}{y - 3} = 5 + \frac{2}{3 - y}$ 有正整数解，那么符合条件的所有整数 $m$ 的和为．

查看试题解析
18. 对于一个四位自然数M ，满足千位上的数字与个位上的数字之和等于百位上的数字与十位上的数字之和，那么就称这个数为“智慧数”．例如， $M = 5241$ ，因为 $5 + 1 = 2 + 4$ ，所以5241是“智慧数”则最小的“智慧数”是；若“智慧数” $M = 1000 a + 100 b + 10 c + d$ ，使二次函数 $y = a x^{2} + (b + c) x + d$ 与x轴有且只有一个交点，且满足 $16 \leq a + b + c + d \leq 25$ ，则满足条件的M的最大值为．

查看试题解析

三、解答题：（本大题8个小题，其中19题8分，其余每小题10分，共78分）

19. 解下列方程：

(1)、 ${(x - 1)}^{2} = 9$ ；

(2)、 $2 x^{2} + 5 x - 12 = 0$ ．

查看试题解析
20. 请完成以下作图和填空：
如图，在 $⊙ O$ 中， $A C$ 为 $⊙ O$ 的直径， $A B$ 为 $⊙ O$ 的弦，点 $E$ 是 $\overset{⌢}{A C}$ 的中点．

(1)、尺规作图：过点 $E$ 作 $A B$ 的垂线交 $⊙ O$ 于点 $N$ ，垂足为点 $M$ ，连接 $C N$ 、 $O E$ ．（只保留作图痕迹）

(2)、求证： $B E = C N$ ．
证明： ∵点E是 $\overset{⌢}{A C}$ 的中点
∴ $\overset{⌢}{A E} =$     ▲
∴ $∠ A O E = ∠ C O E = 90 °$
∴ $∠ A B E = \frac{1}{2} ∠ A O E = 45 °$
∵ $E M ⊥ A B$ ，
∴ $∠ E M B = 90 °$
∴ $∠ B E N = 45 °$
∴ $∠ A B E =$     ▲
∴ $\overset{⌢}{A E} =$     ▲
∴ $\overset{⌢}{C E} = \overset{⌢}{B N}$
∴ $\overset{⌢}{C E} - \overset{⌢}{B C} = \overset{⌢}{B N} - \overset{⌢}{B C}$
∴    ▲
∴ $B E = C N$ ．

查看试题解析
21. $2023$ 年重庆入选“中国研学旅行目的地·标杆城市”，某校为了了解九年级学生对以下哪类研学内容最感兴趣（每人仅选一类）： $A$ ．源远流长的巴渝文化； $B$ ．享誉世界的三峡文化； $C$ ．可歌可泣的抗战文化； $D$ ．感天动地的移民文化．从九年级学生中随机抽取若干名学生进行调查，绘制了如图所示的统计表和扇形统计图（均不完整）．
抽取的学生最感兴趣研学内容统计表如下：
研学内容
人数
频率
$A$
$a$

$B$
$24$

$C$

$b$
$D$
$9$

抽取的学生最感兴趣研学内容扇形统计图如下：
请根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ；

(2)、若该校九年级共有 $540$ 名学生，估计选择“ $C$ ．可歌可泣的抗战文化”的有多少人？

(3)、小聪和小明参加了本次调查，请你用列表或画树状图的方法求他们选择同一类内容的概率．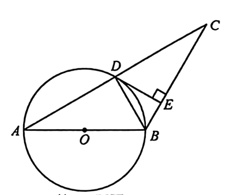

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径， $O A = 2$ ， $∠ A = 30 °$ ， $A C$ 交 $⊙ O$ 于 $D$ ， $D$ 是 $A C$ 的中点， $D E ⊥ B C$ 于点 $E$ ．

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、求 $A C$ 的长．

查看试题解析
23. “当你背单词时，阿拉斯加的鳕鱼正跃出水面；当你算数学时，南太平洋的海鸥正掠过海岸；当你晚自习时，地球的极圈正五彩斑斓；但少年，梦要你亲自实现，那些你觉得看不到的人和遇不到的风景都终将在你生命里出现．”这是直播带货新平台“东方甄选”带货王董宇辉在推销鳕鱼时的台词．所推销鳕鱼的成本为每袋 $50$ 元，当售价为每袋 $90$ 元时，每分钟可销售 $100$ 袋．为了吸引更多顾客，“东方甄选”采取降价措施．据市场调查反映：销售单价每降 $1$ 元，则每分钟可多销售 $10$ 袋．

(1)、每袋鳕鱼的售价为多少元时，每分钟的销量为 $150$ 袋？

(2)、“东方甄选”不忘公益初心，热心教育事业，其决定从每分钟利润中捐出 $500$ 元帮助留守儿童，为了保证捐款后每分钟利润达到 $5500$ 元，且要最大限度让利消费者，求此时鳕鱼的销售单价为多少元？

查看试题解析
24. 如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ， $C E ⊥ A B$ 于点E ， $A E = 8$ ， $B E = C E = 4$ ， $D C = 2$ ．动点P从点A出发，沿 $A \to B$ 方向以每秒2个单位长度的速度运动，同时动点Q从点E出发，沿折线 $E \to C \to D$ 方向以每秒1个单位长度的速度运动．当点Q到达点D时，P、Q两点都停止运动．设动点P运动的时间为x秒， $△ P E Q$ 的面积为y ．

(1)、请直接写出y关于x的函数关系式并注明自变量x的取值范围；

(2)、在给定的平面直角坐标系中，画出这个函数的图象，并写出该函数的一条性质；

(3)、结合函数图象，直接写出 $△ P E Q$ 的面积为4时x的值．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = - \frac{1}{2} x^{2} - x + 4$ 与 $x$ 轴交于 $A$ 、 $B$ 两点（点 $A$ 在点 $B$ 左侧），与 $y$ 轴交于点 $C$ ．连接 $A C$ 、 $B C$ ．

(1)、求 $△ A B C$ 的面积；

(2)、点 $P$ 是直线 $A C$ 上方抛物线上一点，过点 $P$ 作 $P E ⊥ x$ 轴于点 $E$ ，交 $A C$ 于点 $D$ ，求 $P D - \frac{\sqrt{2}}{2} A D$ 的最大值及此时点P的坐标；

(3)、在（2）的条件下，将抛物线向右平移4个单位，向下平移 $4.5$ 个单位，点M为点P的对应点，平移后的抛物线与y轴交于点N ，点Q为平移后的抛物线对称轴上任意一点．写出所有使得以 $Q M$ 为腰的 $△ Q M N$ 是等腰三角形的点Q的坐标，并把求其中一个点Q的坐标的过程写出来．

查看试题解析
26. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D为 $B C$ 边上一动点，连接 $A D$ ，将线段 $A D$ 绕着D点逆时针方向旋转与 $∠ B A C$ 相同的度数得到线段 $D E$ ，连接 $B E$ ．

(1)、如图1，若 $A B = B D$ ，求证： $B E = C D$ ；

(2)、如图2，当 $∠ B A C = 90 °$ 时，连接AE ，将线段 $A E$ 绕着A点逆时针方向旋转 $90 °$ 得到线段 $A F ，$ ，连接 $C F$ ．求证： $A B + C F = \sqrt{2} B D$ ；

(3)、如图3，当 $∠ B A C = 90 °$ 时，若 $A C = 2 \sqrt{2}$ ，连接 $A E$ ，作点C关于 $A E$ 的对称点 $C^{'}$ ，点H是 $B C$ 的中点，连接 $H C^{'}$ ，当 $H C^{'}$ 的长度最大时，直接写出 $B D$ 的长度．

查看试题解析

研学内容	人数	频率
$A$	$a$
$B$	$24$
$C$		$b$
$D$	$9$