重庆市沙坪坝区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-26 类型:期末考试
一、选择题:(本大题10个小题,每小题4分,共40分)
-
1. 4的倒数是( )A、 B、4 C、 D、2. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图, , 若 , 则的度数是( )
3. 如图, , 若 , 则的度数是( ) A、 B、 C、 D、4. 与相似且相似比为 , 则与的周长之比是( )A、 B、 C、 D、5. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、6. 估计的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间7. 由同样长度的木棍按一定的规律组成下列图形,其中第①个图形有5根木棍,第②个图形有9根木棍,第③个图形有13根木棍,…,则第⑦个图形木棍的根数是( )
A、 B、 C、 D、4. 与相似且相似比为 , 则与的周长之比是( )A、 B、 C、 D、5. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、6. 估计的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间7. 由同样长度的木棍按一定的规律组成下列图形,其中第①个图形有5根木棍,第②个图形有9根木棍,第③个图形有13根木棍,…,则第⑦个图形木棍的根数是( ) A、25 B、29 C、33 D、378. 如图,为的直径,与相切于点C , 交的延长线于点D , 若 , , 则线段的长是( )
A、25 B、29 C、33 D、378. 如图,为的直径,与相切于点C , 交的延长线于点D , 若 , , 则线段的长是( )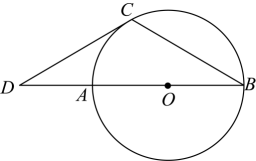 A、3 B、4 C、5 D、69. 如图,在正方形中,点E是上一点,过点E作交于点F , 连接 , , 若 , 则的度数是( )
A、3 B、4 C、5 D、69. 如图,在正方形中,点E是上一点,过点E作交于点F , 连接 , , 若 , 则的度数是( ) A、 B、 C、 D、10. 对于多项式 , 任意选取两个字母分别添加绝对值符号,再互相交换其位置,操作后仍只有减法运算,然后进行去绝对值运算,称此为“绝对互换操作”.例如:选取字母x , y进行“绝对互换操作”得: , 选取字母x , m进行“绝对互换操作”得: .
A、 B、 C、 D、10. 对于多项式 , 任意选取两个字母分别添加绝对值符号,再互相交换其位置,操作后仍只有减法运算,然后进行去绝对值运算,称此为“绝对互换操作”.例如:选取字母x , y进行“绝对互换操作”得: , 选取字母x , m进行“绝对互换操作”得: .下列说法:
①存在“绝对互换操作”,使其运算结果与原多项式相等;②不存在“绝对互换操作”,使其运算结果的值恒大于0;③所有的“绝对互换操作”共有4种不同的运算结果.
其中正确的个数是( )
A、0 B、1 C、2 D、3二、填空题:(本大题8个小题,每小题4分,共32分)
-
11. 计算: .12. 已知一个多边形的每一个外角都等于72°,则这个多边形的边数是.13. 有三张正面分别写有数字1,2,3的卡片,它们除数字外其余完全一样.将其背面朝上洗匀,从中随机抽取一张,记下卡片上的数字后放回洗匀,再从中随机抽取一张,则抽取的两张卡片上的数字相同的概率是 .14. 据统计,沙坪坝区磁器口2023年国庆接待游客约91万人次,2021年国庆接待游客约50万人次,若设2021年国庆至2023年国庆,磁器口接待游客的年平均增长率为x , 根据题意,可列方程为 .15. 如图,在中, , 的平分线交边于点D , 于点E , 点F在边上,若 , , 则线段AB的长是 .
 16. 如图,在矩形中, , , 以点A为圆心,的长为半径画弧交边于点E , 则图中阴影部分的面积是 . (结果保留π)
16. 如图,在矩形中, , , 以点A为圆心,的长为半径画弧交边于点E , 则图中阴影部分的面积是 . (结果保留π)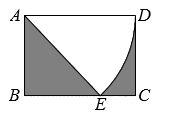 17. 已知关于x的分式方程的解为整数,且关于y的不等式组有且仅有3个整数解,则所有满足条件的整数m的值之和是 .18. 如果一个四位自然数的各数位上的数字互不相等且均不为0,满足 , 那么称这个四位数为“和方数”.例如:四位数2613,因为 , 所以2613是“和方数”;四位数2514,因为 , 所以2514不是“和方数”.若是“和方数”,则这个数是;若四位数M是“和方数”,将“和方数”M的千位数字与百位数字对调,十位数字与个位数字对调,得到新数N , 若能被33整除,则满足条件的M的最大值是 .
17. 已知关于x的分式方程的解为整数,且关于y的不等式组有且仅有3个整数解,则所有满足条件的整数m的值之和是 .18. 如果一个四位自然数的各数位上的数字互不相等且均不为0,满足 , 那么称这个四位数为“和方数”.例如:四位数2613,因为 , 所以2613是“和方数”;四位数2514,因为 , 所以2514不是“和方数”.若是“和方数”,则这个数是;若四位数M是“和方数”,将“和方数”M的千位数字与百位数字对调,十位数字与个位数字对调,得到新数N , 若能被33整除,则满足条件的M的最大值是 .三、解答题:(本大题8个小题,共78分)
-
19. 计算:(1)、;(2)、 .20. 学习了平行四边形后,小庆进行了拓展性探究.他发现,过一个顶点同时向平行四边形的两边作垂线段,如果这两条垂线段相等,那么这个平行四边行是菱形.其解决问题的思路是通过证明平行四边行的一组邻边所在的三角形全等即可得出结论.
请根据他的思路完成以下作图和填空.
用直尺和圆规,过点C作边上的垂线,垂足为点F . (只保留作图痕迹)
已知:如图,在中,于点E , 于点F , .

求证:四边形是菱形.
证明:∵四边形是平行四边形,
∴ ▲ .
又∵ , ,
∴ .
又∵ ▲ ,
∴ ▲
∴ ▲ .
又∵四边形是平行四边形,
∴四边形是菱形.
21. 科教兴国,科普为先.某校组织七、八年级学生参加了“科普赋能,智行未来”科普知识竞赛.现从该校七、八年级学生中分别随机抽取了20名学生的竞赛成绩进行整理,描述和分析(成绩得分用x表示,共分为五组: , 下面给出了部分信息:七年级20名学生的成绩是:69,76,78,79,82,84,85,86,86,86,86,88,88,90,92,92,95,98,100,100.
八年级20名学生的成绩在C组中的数据是:83,85,85,86,87,89,89,89,89.
七、八两年级抽取的学生成绩数据统计表
班级
平均数
中位数
众数
满分率
七年级
87
86
a
八年级
87
b
89
八年级抽取的学生成绩扇形统计图

根据以上信息,解答下列问题:
(1)、直接写出图表中a、b、m的值: , , ;(2)、根据以上数据,你认为七年级和八年级中哪个年级的学生掌握科普知识较好?请说明理由(一条理由即可);(3)、该校七年级有400名学生和八年级有500名学生参加了此次科普知识竞赛,请估计两个年级成绩达到90分及以上的学生共有多少人?22. 山城步道是重庆的特色,市民可以在步道里面休闲、运动,享受美好生活.半山崖线步道沙坪坝段全长2000米,由甲、乙两个工程队合作完成,甲工程队修建的步道长度比乙工程队修建的步道长度的2倍少400米.(1)、求甲、乙两工程队各修建步道多少米?(2)、实际修建过程中,甲工程队每天比乙工程队多修5米,最终甲工程队完成任务时间是乙工程队完成任务时间的倍,则甲工程队每天修建步道多少米?23. 如图,在中, , , . 点是中点,动点 , 分别以每秒1个单位长度的速度同时运动,点从点出发,沿直线运动,到达点时停止运动,点从点出发,沿折线运动,到达点时停止运动.设点 , 点的运动时间为秒,点 , 之间的距离为 . (1)、请直接写出y与x之间的函数表达式并注明自变量x的取值范围;(2)、在给定的平面直角坐标系中画出这个函数图象,并写出该函数的一条性质;(3)、结合函数图象,写出P , Q两点相距2个位长度时x的值.24. 为了满足市民健身需求,市政部门在某公园内沿湖边修建了四边形循环步道,如图,经勘测,点在点的正南方,点在点的正东方,点在点的东北方向,点在点的南偏西方向,点在点的北偏西方向米处.(参考数据: , , )
(1)、请直接写出y与x之间的函数表达式并注明自变量x的取值范围;(2)、在给定的平面直角坐标系中画出这个函数图象,并写出该函数的一条性质;(3)、结合函数图象,写出P , Q两点相距2个位长度时x的值.24. 为了满足市民健身需求,市政部门在某公园内沿湖边修建了四边形循环步道,如图,经勘测,点在点的正南方,点在点的正东方,点在点的东北方向,点在点的南偏西方向,点在点的北偏西方向米处.(参考数据: , , ) (1)、求的长度(结果精确到米);(2)、小沙准备从点跑步到点去见小渝,小沙决定选择一条较短线路,请计算说明小沙应选择路线,还是路线?25. 如图,在平面直角坐标系中,抛物线交x轴于 , B两点,交y轴于点 .
(1)、求的长度(结果精确到米);(2)、小沙准备从点跑步到点去见小渝,小沙决定选择一条较短线路,请计算说明小沙应选择路线,还是路线?25. 如图,在平面直角坐标系中,抛物线交x轴于 , B两点,交y轴于点 .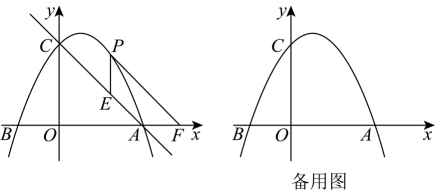 (1)、求抛物线的表达式;(2)、点P是直线上方抛物线上的一动点,过点P作y轴的平行线交于点E , 过点P作的平行线交x轴于点F , 求的最大值及此时点P的坐标;(3)、将该抛物线y沿射线方向平移个单位长度得到新抛物线 , 点G是新抛物线的顶点,点M为新抛物线的对称轴上一点,在平面内确定一点N , 使得以点C , G , M , N为顶点的四边形是以为边的菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.26. 在中, , D是边上一动点,E是外一点,连接 .
(1)、求抛物线的表达式;(2)、点P是直线上方抛物线上的一动点,过点P作y轴的平行线交于点E , 过点P作的平行线交x轴于点F , 求的最大值及此时点P的坐标;(3)、将该抛物线y沿射线方向平移个单位长度得到新抛物线 , 点G是新抛物线的顶点,点M为新抛物线的对称轴上一点,在平面内确定一点N , 使得以点C , G , M , N为顶点的四边形是以为边的菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.26. 在中, , D是边上一动点,E是外一点,连接 . (1)、如图1, , , 若 , 求的度数;(2)、如图2, , , 过点D作交于点F , 若 , 求证:;(3)、如图3, , 延长交的延长线于点F , 交于点G , 点D是直线上一动点,将沿翻折得 , 连接 , 取的中点M , 连接 , 若 , 当线段取得最大值时,请直接写出的值.
(1)、如图1, , , 若 , 求的度数;(2)、如图2, , , 过点D作交于点F , 若 , 求证:;(3)、如图3, , 延长交的延长线于点F , 交于点G , 点D是直线上一动点,将沿翻折得 , 连接 , 取的中点M , 连接 , 若 , 当线段取得最大值时,请直接写出的值.