贵州省毕节市2022年中考数学模拟试卷(一)
试卷更新日期:2024-03-26 类型:中考模拟
一、选择题(本题共15小题,共45分)
-
1. 计算的结果是A、 B、 C、 D、2. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1053. 下列计算正确的是A、 B、 C、 D、4. 下列四个图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
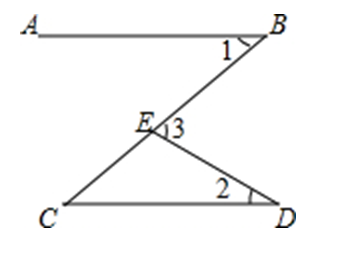
D、 5. 如图,AB//CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
5. 如图,AB//CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
 A、70° B、60° C、55° D、50°6. 不等式组的解集在数轴上表示正确的是( )A、
A、70° B、60° C、55° D、50°6. 不等式组的解集在数轴上表示正确的是( )A、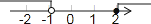 B、
B、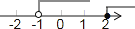 C、
C、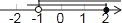 D、
D、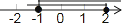 7. 一元二次方程的根的情况是( )
7. 一元二次方程的根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定8. 在某校开展的“厉行节约,你我有责”活动中,七年级某班对学生7天内收集饮料瓶的情况统计如下(单位:个):76,90,64,100,84,64,73.则这组数据的众数和中位数分别是( )A、64,100 B、64,76 C、76,64 D、64,849. 如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )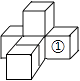 A、主视图改变,左视图改变 B、俯视图不变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图不变10. 在平面直角坐标系中,已知点 , , 以原点为位似中心,相似比为 , 把缩小,则点的对应点的坐标是A、 B、 C、或 D、或11. 为了节省空间,家里的饭碗一般是摞起来存放的.如果6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,那么11只饭碗摞起来的高度更接近( )A、21cm B、22cm C、23cm D、24cm12. 函数 与 (k≠0)在同一直角坐标系中的图象可能是( )A、
A、主视图改变,左视图改变 B、俯视图不变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图不变10. 在平面直角坐标系中,已知点 , , 以原点为位似中心,相似比为 , 把缩小,则点的对应点的坐标是A、 B、 C、或 D、或11. 为了节省空间,家里的饭碗一般是摞起来存放的.如果6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,那么11只饭碗摞起来的高度更接近( )A、21cm B、22cm C、23cm D、24cm12. 函数 与 (k≠0)在同一直角坐标系中的图象可能是( )A、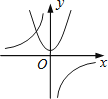 B、
B、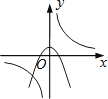 C、
C、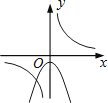 D、
D、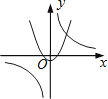 13. 如图,已知的周长为 , 的长为 , 则图中阴影部分的面积为
13. 如图,已知的周长为 , 的长为 , 则图中阴影部分的面积为 A、 B、 C、 D、14. 如图,中, , 在同一平面内,将绕点旋转到的位置,使得 , 则等于
A、 B、 C、 D、14. 如图,中, , 在同一平面内,将绕点旋转到的位置,使得 , 则等于 A、 B、 C、 D、15. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点 , 过点作轴,垂足为 , 且 , 则以下结论:
A、 B、 C、 D、15. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点 , 过点作轴,垂足为 , 且 , 则以下结论:
;
当时,;
如图,当时,;
当时,随的增大而增大,随的增大而减小.
其中正确结论的个数是 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共5小题,共15分)
-
16. 若代数式有意义,则实数x的取值范围是 .
17. 分解因式: .18. 已知△ABC∽△DEF,其中AB=5,BC=6,CA=9,DE=3,那么△DEF的周长是 .19. 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行海里可使渔船到达离灯塔距离最近的位置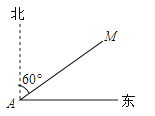 20. 如图,反比例函数的图象交的斜边于点 , 交直角边于点 , 点在轴上.若的面积为 , :: , 则的值为 .
20. 如图,反比例函数的图象交的斜边于点 , 交直角边于点 , 点在轴上.若的面积为 , :: , 则的值为 .
三、计算题(本题共1小题,共8分)
-
21. 计算:
四、解答题(本题共6小题,共72分)
-
22. 先化简 , 然后从 , , , 四个数中选择一个合适的数作为的值代入求值.23. 某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题:
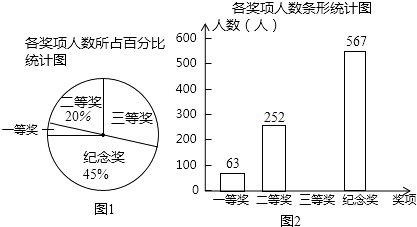 (1)、该校共有名学生;(2)、在图①中,“三等奖”所对应扇形的圆心角度数是;(3)、将图②补充完整;(4)、从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.24. 阅读下面材料:小腾遇到这样一个问题:如图 , 在中,点在线段上, , , , , 求的长.
(1)、该校共有名学生;(2)、在图①中,“三等奖”所对应扇形的圆心角度数是;(3)、将图②补充完整;(4)、从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.24. 阅读下面材料:小腾遇到这样一个问题:如图 , 在中,点在线段上, , , , , 求的长.
小腾发现,过点作 , 交的延长线于点 , 通过构造 , 经过推理和计算能够使问题得到解决如图 .
请回答:(1)、的度数为 , 的长为 .
(2)、参考小腾思考问题的方法,解决问题:
如图 , 在四边形中, , , , 与交于点 , , , 求的长.25. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.(1)、请直接写出y与x的函数关系式;(2)、当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)、设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?26. 如图,在中,以为直径的交于点 , 过点作于点 , 且 . (1)、判断与的位置关系并说明理由;(2)、若 , , 求的半径.27. 如图,抛物线交轴于点 , 交轴于点 , 已知经过点 , 的直线的表达式为 .
(1)、判断与的位置关系并说明理由;(2)、若 , , 求的半径.27. 如图,抛物线交轴于点 , 交轴于点 , 已知经过点 , 的直线的表达式为 . (1)、求抛物线的函数表达式及其顶点的坐标;(2)、如图 , 点是线段上的一个动点,其中 , 作直线轴,交直线于 , 交抛物线于 , 作轴,交直线于点 , 四边形为矩形.设矩形的周长为 , 写出与的函数关系式,并求为何值时周长最大;
(1)、求抛物线的函数表达式及其顶点的坐标;(2)、如图 , 点是线段上的一个动点,其中 , 作直线轴,交直线于 , 交抛物线于 , 作轴,交直线于点 , 四边形为矩形.设矩形的周长为 , 写出与的函数关系式,并求为何值时周长最大;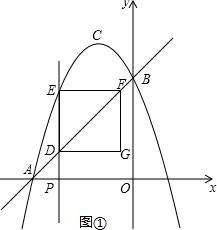 (3)、如图 , 在抛物线的对称轴上是否存在点 , 使点 , , 构成的三角形是以为腰的等腰三角形?若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.
(3)、如图 , 在抛物线的对称轴上是否存在点 , 使点 , , 构成的三角形是以为腰的等腰三角形?若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.
-