贵州省毕节市2022年中考数学模拟试卷(二)
试卷更新日期:2024-03-26 类型:中考模拟
一、选择题(共15小题,共45分)
-
1. 的倒数的相反数是( )A、 B、 C、 D、2. 如图是一个由7个相同正方体组合而成的几何体,它的主视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图形既是轴对称图形又是中心对称图形的是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图形既是轴对称图形又是中心对称图形的是( )A、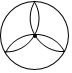 B、
B、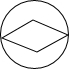 C、
C、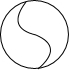 D、
D、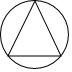 5. 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
5. 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( ) A、∠B B、∠A C、∠EMF D、∠AFB6. 使分式有意义的x的取值范围是( )A、x=2 B、x≠2 C、x=-2 D、x≠-27. 如图,直线 , , , 则等于( )
A、∠B B、∠A C、∠EMF D、∠AFB6. 使分式有意义的x的取值范围是( )A、x=2 B、x≠2 C、x=-2 D、x≠-27. 如图,直线 , , , 则等于( ) A、 B、 C、 D、8. 小红同学四次中考数学模拟考试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )A、平均数是105 B、众数是104 C、中位数是104 D、方差是509. 已知等腰三角形的腰和底的长分别是一元二次方程的根,则该三角形的周长为( )A、 B、 C、或 D、10. 某科研小组,为了考查某水库野生鱼的数量,从中捕捞100条,作上标记后,放回水库,经过一段时间,再从中捕捞300条,发现有标记的鱼有15条,则估计该水库中有野生鱼( )A、8000条 B、4000条 C、2000条 D、1000条11. 程大位直指算法统宗:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.意思是:有个和尚分个馒头,如果大和尚人分个,小和尚人分个,正好分完.试问大、小和尚各多少人?设大和尚有人,依题意列方程得( )A、 B、 C、 D、12. 如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A、 B、 C、 D、8. 小红同学四次中考数学模拟考试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )A、平均数是105 B、众数是104 C、中位数是104 D、方差是509. 已知等腰三角形的腰和底的长分别是一元二次方程的根,则该三角形的周长为( )A、 B、 C、或 D、10. 某科研小组,为了考查某水库野生鱼的数量,从中捕捞100条,作上标记后,放回水库,经过一段时间,再从中捕捞300条,发现有标记的鱼有15条,则估计该水库中有野生鱼( )A、8000条 B、4000条 C、2000条 D、1000条11. 程大位直指算法统宗:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.意思是:有个和尚分个馒头,如果大和尚人分个,小和尚人分个,正好分完.试问大、小和尚各多少人?设大和尚有人,依题意列方程得( )A、 B、 C、 D、12. 如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( ) A、50° B、40° C、30° D、25°13. 如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A、50° B、40° C、30° D、25°13. 如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( ) A、3cm B、4cm C、5cm D、8cm14. 已知反比例函数的图象如图所示,则二次函数的图象大致为( )
A、3cm B、4cm C、5cm D、8cm14. 已知反比例函数的图象如图所示,则二次函数的图象大致为( ) A、
A、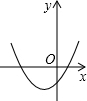 B、
B、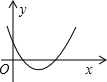 C、
C、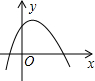 D、
D、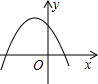 15. 如图,抛物线的对称轴为 , 与轴的一个交点在和之间,其部分图象如图所示,则下列结论:
15. 如图,抛物线的对称轴为 , 与轴的一个交点在和之间,其部分图象如图所示,则下列结论:
点、、是该抛物线上的点,则
为任意实数
⑥
其中正确结论的个数是( )A、 B、 C、 D、二、填空题(共5小题,共25分)
-
16. 若两个互补的角的度数之比为: , 则这两个角中较小角的度数是 度.17. 苹果的进价为每千克3.8元,销售中估计有5%的苹果正常损耗,为避免亏本,商家把售价应该至少定为每千克元.
18. 已知一个围棋盒子中装有7颗围棋子,其中3颗白棋子,4颗黑棋子,若往盒子中再放入x颗白棋子和y颗黑棋子,从盒子中随机取出一颗白棋子的概率为 ,则y与x之间的关系式是 .19. 如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,M是AF的中点,连接BM,则sin∠ABM= .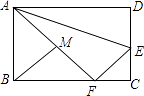 20. 如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2 ,反比例函数y= 的图象经过点B,则k的值为 .
20. 如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2 ,反比例函数y= 的图象经过点B,则k的值为 .
三、计算题(本题共1小题,共10分)
-
21. 计算:
四、解答题(本题共6小题,共70分)
-
22. 先化简: , 再求当与互为相反数时代数式的值.23. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
请结合图表完成下列各题:
 (1)、①求表中a的值;②频数分布直方图补充完整;(2)、若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?(3)、第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.24. 如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)、①求表中a的值;②频数分布直方图补充完整;(2)、若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?(3)、第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.24. 如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.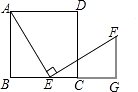 (1)、求证:△ABE≌△EGF;(2)、若AB=2,S△ABE=2S△ECF , 求BE.25. 某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.26. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)、求证:△ABE≌△EGF;(2)、若AB=2,S△ABE=2S△ECF , 求BE.25. 某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.26. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.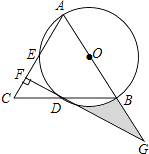 (1)、求证:DF是⊙O的切线;(2)、若CF=1,DF= ,求图中阴影部分的面积.27. 如图注:与图完全相同 , 二次函数的图象与轴交于 , 两点,与轴交于点 .
(1)、求证:DF是⊙O的切线;(2)、若CF=1,DF= ,求图中阴影部分的面积.27. 如图注:与图完全相同 , 二次函数的图象与轴交于 , 两点,与轴交于点 . (1)、求该二次函数的解析式;(2)、设该抛物线的顶点为 , 求的面积请在图中探索;(3)、若点 , 同时从点出发,都以每秒个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动,当 , 运动到秒时,沿所在的直线翻折,点恰好落在抛物线上点处,请直接判定此时四边形的形状,并求出点坐标请在图中探索 .
(1)、求该二次函数的解析式;(2)、设该抛物线的顶点为 , 求的面积请在图中探索;(3)、若点 , 同时从点出发,都以每秒个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动,当 , 运动到秒时,沿所在的直线翻折,点恰好落在抛物线上点处,请直接判定此时四边形的形状,并求出点坐标请在图中探索 .
-