贵州省毕节市威宁县2022年中考数学模拟试题 (二)
试卷更新日期:2024-03-26 类型:中考模拟
一、选择题(共15小题,共45分)
-
1. 计算的结果为( )A、 B、2 C、 D、42. 1月20日湖北省统计局发布数据:根据地区生产总值统一核算结果,2021年全省地区生产总值超过5万亿元,达到50012.94亿元.“50012.94”用科学记数法表示为( ).A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列品牌的标识中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,在△ABC中,AB=AC,直线DE,FG分别经过点B,C,DE∥FG.若∠DBC=45°,∠ACG=10°,则∠ABE的度数为( )
5. 如图,在△ABC中,AB=AC,直线DE,FG分别经过点B,C,DE∥FG.若∠DBC=45°,∠ACG=10°,则∠ABE的度数为( ) A、100° B、105° C、110° D、115°6. 若关于x的不等式组无解,且关于y的分式方程的解是正数,则满足条件的整数m的值之和是( )A、 B、 C、 D、7. 定义新运算“”:对于任意实数a , b , 都有 . 例: . 则方程的根的情况为( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根8. 小明连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3,关于这组数据,下列说法正确的是( )A、众数是36.2℃ B、中位数是36.5℃ C、平均数是36.2℃ D、极差是0.3℃9. 如图是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
A、100° B、105° C、110° D、115°6. 若关于x的不等式组无解,且关于y的分式方程的解是正数,则满足条件的整数m的值之和是( )A、 B、 C、 D、7. 定义新运算“”:对于任意实数a , b , 都有 . 例: . 则方程的根的情况为( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根8. 小明连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3,关于这组数据,下列说法正确的是( )A、众数是36.2℃ B、中位数是36.5℃ C、平均数是36.2℃ D、极差是0.3℃9. 如图是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )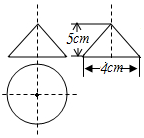 A、 B、 C、 D、10. 如图,在网格图中,每个小正方形边长均为1,点和的顶点均为小正方形的顶点,以O为位似中心,在网络图中作 , 使和位似,且位似比为1∶2;连接(1)中的 , 则四边形的周长为( ).
A、 B、 C、 D、10. 如图,在网格图中,每个小正方形边长均为1,点和的顶点均为小正方形的顶点,以O为位似中心,在网络图中作 , 使和位似,且位似比为1∶2;连接(1)中的 , 则四边形的周长为( ). A、 B、 C、 D、11. 佳佳坐在匀速行驶的车上,将每隔一段时间看到的里程碑上的数描述如下:
A、 B、 C、 D、11. 佳佳坐在匀速行驶的车上,将每隔一段时间看到的里程碑上的数描述如下:时刻
12:00
13:00
14:00
里程碑上的数
是一个两位数,数字之和为7
十位数字和个位数字与12:00时看到的刚好相反
比12:00看到的两位数中间多了个0
则12:00时看到的两位数是( )
A、16 B、25 C、34 D、5212. 已知反比例函数的图象如图所示,则一次函数y=ax+c和二次函数y=cx2+bx+a在同一直角坐标系中的图象可能是( )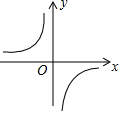 A、
A、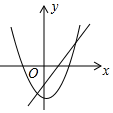 B、
B、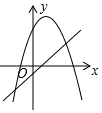 C、
C、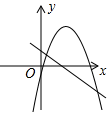 D、
D、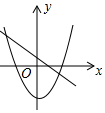 13. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( )
13. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( ) A、 B、 C、8 D、1014. 如图,在中, , , 为边的中点,平分 , 交于点 , 交于点 , 则的度数为( )
A、 B、 C、8 D、1014. 如图,在中, , , 为边的中点,平分 , 交于点 , 交于点 , 则的度数为( )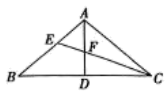 A、130° B、120° C、110° D、100°15. 如图,直线与抛物线交于A , B两点,且点A的横坐标是-1,点B的横坐标是4,有以下结论:①若点A在轴上,则抛物线与轴的另一个交点坐标为(3,0);②当时,一次函数与二次函数的函数值都随的增大而增大;③的长度可以等于5,其中正确的结论有( )
A、130° B、120° C、110° D、100°15. 如图,直线与抛物线交于A , B两点,且点A的横坐标是-1,点B的横坐标是4,有以下结论:①若点A在轴上,则抛物线与轴的另一个交点坐标为(3,0);②当时,一次函数与二次函数的函数值都随的增大而增大;③的长度可以等于5,其中正确的结论有( ) A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题(共5小题,共25分)
-
16. 若代数式有意义,则x的取值范围为 .17. 一个长方形的长为 , 宽为 , 则这个长方形的面积是 .18. 如图,小明从路灯下处,向前走了5米到达处,在处发现自己在地面上的影子长是2米,如果小明的身高为1.7米,那么路灯离地面的高度是米.
 19. 在Rt△ABC中,∠C=90°,cosA= , AC= , 则BC的长为 .20. 如图,点A是反比例函数()图象上一点,轴于点且与反比例函数()的图象交于点B , , 连接 , , 若的面积为8,则 .
19. 在Rt△ABC中,∠C=90°,cosA= , AC= , 则BC的长为 .20. 如图,点A是反比例函数()图象上一点,轴于点且与反比例函数()的图象交于点B , , 连接 , , 若的面积为8,则 .
三、计算题
-
21. 计算: .
四、解答题(本题共6小题,共70分)
-
22. 先化简, , 然后从范围内选取一个合适的整数作为x的值代入求值.23. 眉山天府新区某学校创办“耕耘文学社”以来,关注度逐年上升.学校为了了解学生对“耕耘文学社”的关注度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.(其中A表示“关注”;B表示“不关注”;C表示“非常关注”;D表示“关注很少”)请你根据统计图中所提供的信息解答下列问题:
 (1)、请补全条形统计图 , 直接写出;(2)、该校现有学生420名,请估计这420名学生中“非常关注”的学生人数;(3)、在一次交流活动中,老师决定从本次调查回答“不关注”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“不关注”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率.24.
(1)、请补全条形统计图 , 直接写出;(2)、该校现有学生420名,请估计这420名学生中“非常关注”的学生人数;(3)、在一次交流活动中,老师决定从本次调查回答“不关注”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“不关注”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率.24. (1)、问题发现
(1)、问题发现如图1,在中, , D是线段上一动点,以为一条边在A的左侧作 , 使 , 连接 . 则与的数量关系为 .
(2)、类比探究如图2,在中,D是线段上一动点,以为一条边在的左侧作 , 使且 , 连接 . 则(1)中与的数量关系仍然成立吗?请说明理由.
(3)、拓展应用如图3,在(2)的条件下,若 , , 当取最小值时,的面积为 .
25. 铁棍山药上有像铁锈一样的痕迹.故得名铁棍山药.某网店购进铁根山药若干箱.物价部门规定其销售单价不高于元箱,经市场调查发现:销件单价定为元箱时,每日销售箱;如调整价格,每降价元箱,每日可多销售箱.(1)、已知某天售出铁棍山药箱,则当天的销售单价为元箱.(2)、该网店现有员工名.每天支付员工的工资为每人每天元,每天平均支付运费及其他费用元,当某天的销售价为元箱时,收支恰好平衡.①铁棍山药的进价;
②若网店每天的纯利润收入支出全部用来偿还一笔元的贷款,则至少需多少天才能还清贷款?
26. 如图,四边形内接于半 , 是半的直径,A、D是半圆弧的三等分点连接 , 过D作交的延长线于E. (1)、求证:是半的切线;(2)、已知 , 求图中阴影部分的面积.27. 如图,某体育休闲中心的一处山坡的坡度为1∶2,山坡上A处的水平距离 , A处有一根与垂直的立杆 . 这是投掷沙球的比赛场地,要求人站在立杆正前方的山坡下点O处投掷沙球,沙球超过立杆的高度即为获胜.
(1)、求证:是半的切线;(2)、已知 , 求图中阴影部分的面积.27. 如图,某体育休闲中心的一处山坡的坡度为1∶2,山坡上A处的水平距离 , A处有一根与垂直的立杆 . 这是投掷沙球的比赛场地,要求人站在立杆正前方的山坡下点O处投掷沙球,沙球超过立杆的高度即为获胜.在一次比赛中,小林投出的沙球运动路线看作一条抛物线,沙球出手时离地面 , 当飞行的最大高度为时,它的水平飞行距离为;
 (1)、求该抛物线的表达式,并在网格图中,以O为原点建立平面直角坐标系,画出这条抛物线的大致图像;(2)、小林这一次投掷沙球能否获胜?请说明理由.
(1)、求该抛物线的表达式,并在网格图中,以O为原点建立平面直角坐标系,画出这条抛物线的大致图像;(2)、小林这一次投掷沙球能否获胜?请说明理由.
-